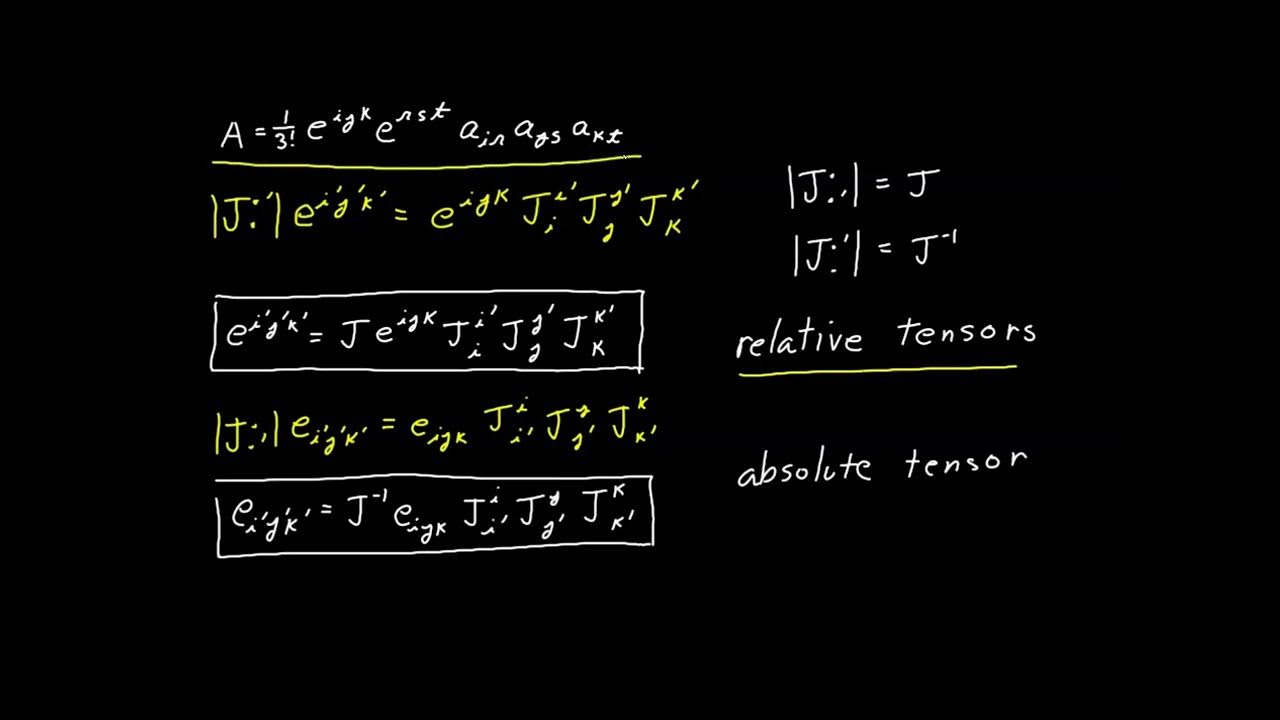Video 44 - Determinants
TLDRThis video from a tensor calculus series explains the syntax for calculating determinants, a scalar value derived from a square matrix. It starts with the Leibniz formula for a 3x3 matrix, illustrating the process with a step-by-step example. The video then discusses the permutation symbol and skew symmetry in tensor notation, leading to a general formula for determinants in tensor calculus. It concludes by showing how to apply this formula to different index structures, emphasizing the importance of maintaining index consistency and the applicability of determinants to any two-dimensional matrix, regardless of tensor status.
Takeaways
- 📚 The determinant is a scalar function calculated from a square matrix or array of numbers, which can be represented with indices i and j.
- 🔍 The script introduces the Leibniz formula, which is a method to calculate the determinant of a square matrix using permutations of indices.
- 👉 The determinant of a 3x3 matrix is explained step-by-step, demonstrating how to sum products of elements along diagonals with alternating signs.
- 🔢 The script explains the concept of symmetry groups (Sn) and permutations (σ), which are essential for understanding the Leibniz formula.
- 🌐 The permutation symbol (ε) is used to simplify the determinant calculation in tensor calculus, capturing the sign changes due to permutations.
- 🔄 The upper indices in the determinant expression exhibit skew symmetry, which is crucial for the correct calculation of the determinant in tensor notation.
- 📉 The script demonstrates how to improve the determinant expression by removing hard-coded indices and using tensor calculus rules for index renaming.
- 📈 A final expression for the determinant in tensor calculus is derived, which is a full contraction involving the permutation symbol and matrix elements.
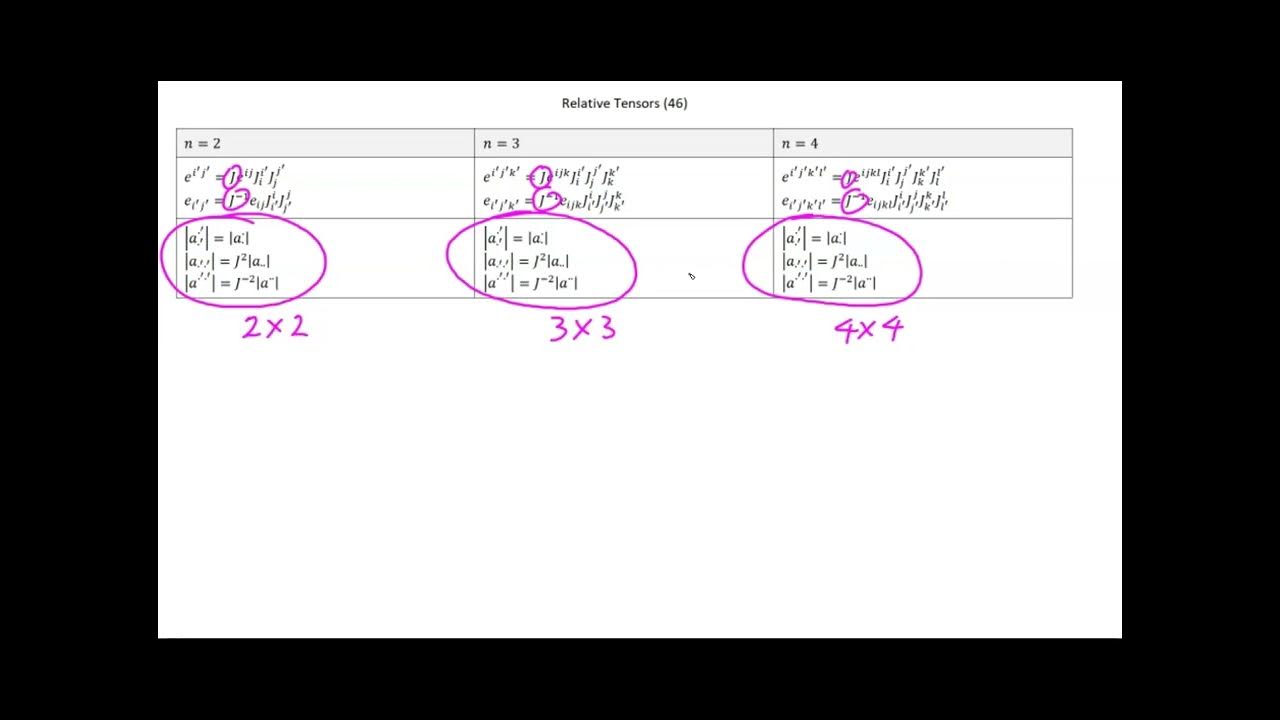
- 📝 The determinant expressions are generalized for different index structures, including one upper and one lower index, two lower indices, or two upper indices.
- 📚 The script concludes by emphasizing that the determinant applies to any two-dimensional matrix, regardless of the index structure, and that the permutation symbols must match the index structure used.
- 🧩 The video also discusses the concept of tensors, suggesting that the determinant expressions could be part of a broader tensor calculus framework, although the nature of tensors is a topic for another video.
Q & A
What is the determinant in the context of tensor calculus?
-The determinant is a function that takes a square matrix or an array of numbers as input and produces a single scalar value as output. It can be represented using various notations, such as det(A) or with the symbol inside brackets, and is fundamental in tensor calculus for handling arrays with indices.
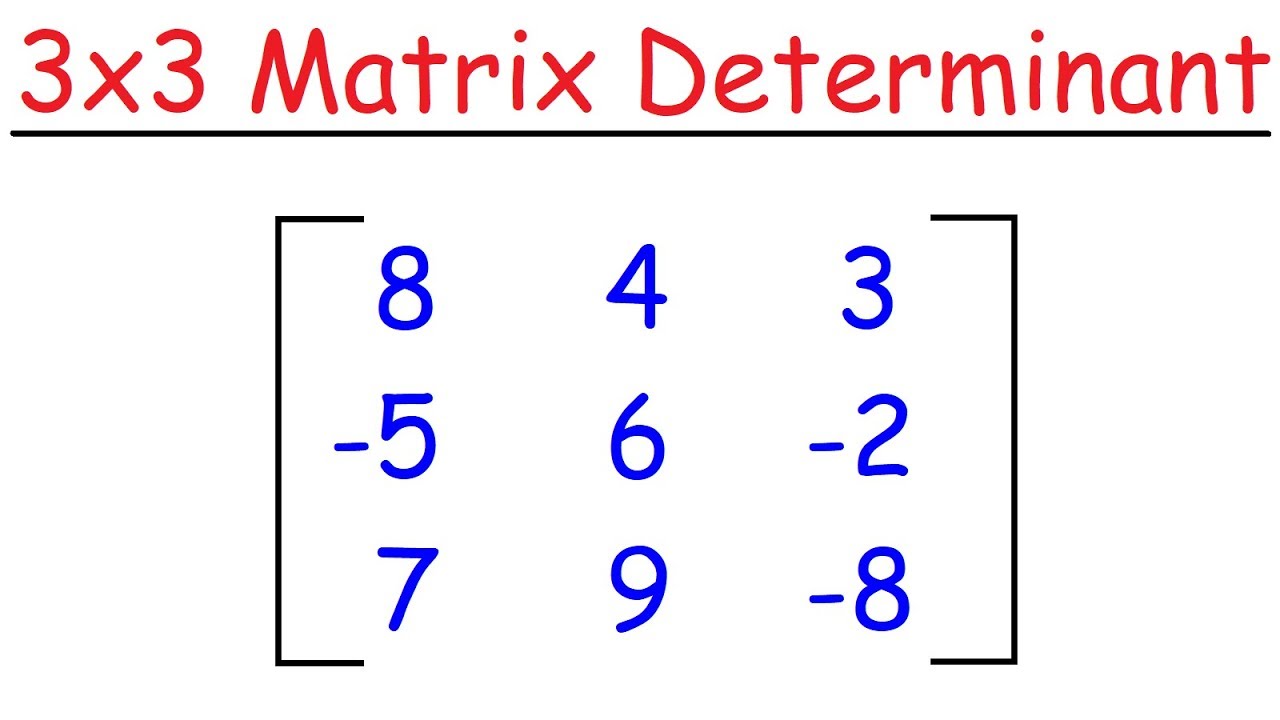
How is the determinant of a 3x3 matrix calculated traditionally?
-Traditionally, the determinant of a 3x3 matrix is calculated by extending the first two columns to the right and then summing up a series of terms determined by drawing diagonal lines across the matrix. Each term involves a product of three matrix elements along these diagonals, with alternating signs.
What is the Leibniz formula and how does it relate to the determinant?
-The Leibniz formula is a method for calculating the determinant of a square matrix using permutations of indices. It involves summing the product of matrix elements for all possible permutations of the indices, with a sign determined by whether the permutation is even or odd.
What is a symmetry group in the context of the Leibniz formula?
-A symmetry group, denoted by 'sn', is a set of numbers used in the Leibniz formula to designate the indices of the matrix. For example, 's3' would be the set of numbers {1, 2, 3}, and the formula iterates through all possible permutations of these numbers.
How does the permutation symbol eijk work in tensor calculus?
-The permutation symbol eijk in tensor calculus is used to account for the sign of the product in the determinant calculation. It is equal to +1 for even permutations and -1 for odd permutations of the indices i, j, and k.
What is meant by 'skew symmetry' in the context of tensor calculus?
-Skew symmetry in tensor calculus refers to the property that switching two indices in a term changes the sign of the term. This property is exhibited by the upper indices in the determinant expression and is crucial for the correct calculation of the determinant.
How can the determinant be expressed in a form that is more suitable for tensor calculus?
-The determinant can be expressed in a form that is more suitable for tensor calculus by using permutation symbols and introducing free indices. This allows for a full contraction that results in a scalar value, without hard-coding specific index values, and adheres to tensor calculus syntax.
What is the significance of the full contraction in the determinant expression?
-The full contraction in the determinant expression is significant because it allows for the calculation of the determinant using tensor calculus rules. It ensures that the expression results in a scalar value and can be integrated into other tensor equations.
Why is the final determinant expression divided by 6?
-The final determinant expression is divided by 6 because there are 3! (3 factorial) permutations of the indices, and each permutation contributes to the determinant calculation. Dividing by 6 normalizes the expression to give the correct determinant value.
How does the script handle different index structures for calculating the determinant?
-The script provides expressions for calculating the determinant for different index structures, including those with one upper and one lower index, two lower indices, and two upper indices. It emphasizes the importance of using the correct permutation symbols to match the index structure in the determinant calculation.
Outlines
📚 Introduction to Tensor Calculus and Determinants
This paragraph introduces the topic of the video, which is the syntax used in tensor calculus to represent determinants. It explains that the determinant is a function of a square matrix, which can be represented using indices. The output of this function is a scalar value, and the paragraph outlines various notations for representing the determinant. It also mentions the Leibniz formula, a common method for calculating the determinant of a matrix, and suggests a practical approach to understanding it by starting with a 3x3 matrix example.
🔍 Exploring the Leibniz Formula and 3x3 Matrix Determinants
The paragraph delves into the specifics of calculating the determinant of a 3x3 matrix using the Leibniz formula. It describes the process of extending the matrix and calculating the determinant by forming diagonal products with alternating signs. The explanation includes the formation of terms and how to apply the formula to achieve the determinant. It also touches on alternative methods for calculating determinants but emphasizes the Leibniz formula's role in understanding the process.
🔄 Understanding Symmetry Groups and Permutations in Determinants
This section explains the concept of symmetry groups and permutations as they relate to the Leibniz formula. It describes how the determinant is calculated by considering all possible permutations of the indices within a symmetry group, with each permutation contributing a term to the determinant calculation. The paragraph illustrates this with the example of symmetry group three, detailing how the sigma symbol iterates through the permutations and how the sign of each term is determined by whether the permutation is even or odd.
📘 Tensor Calculus Expressions for Determinants
The paragraph introduces the tensor calculus approach to expressing determinants, focusing on the use of the permutation symbol and the concept of contraction. It discusses how the permutation symbol accounts for the skew symmetry of the indices and how the contraction process simplifies the expression to a scalar value. The explanation includes the transformation of the original 3x3 determinant expression into a tensor calculus form that eliminates hard-coded indices and aligns with tensor notation.
🌐 Generalizing Determinant Expressions for Tensor Calculus
This section generalizes the determinant expressions for tensor calculus to accommodate different index structures, including those with two lower or two upper indices. It emphasizes the importance of using the correct permutation symbols to ensure the determinant expressions result in a scalar value. The paragraph concludes by reiterating that the determinant applies to any two-dimensional matrix, regardless of the index configuration, and that the expressions provided are valid for calculating determinants in tensor calculus.
🔚 Recap and Conclusion on Determinants in Tensor Calculus
The final paragraph provides a recap of the video's main points, summarizing the process of finding the determinant of a doubly indexed system using the Leibniz formula and tensor calculus. It highlights the use of permutation symbols to capture the relationship between the determinant and its components and explains how the skew symmetry of the indices is accounted for in the expressions. The paragraph concludes by emphasizing the correctness and consistency of the determinant expressions with tensor calculus syntax.
Mindmap
Keywords
💡Tensor Calculus
💡Determinant
💡Leibniz Formula
💡Permutation
💡Scalar Value
💡Skew Symmetry
💡Permutation Symbol
💡Full Contraction
💡Matrix
💡Index Structures
Highlights
Introduction to the concept of determinants in tensor calculus and their representation using indices.
Explanation of determinants as a scalar value output from a square matrix input.
Different notations for representing determinants, including det(A) and scalar value representations.
Leibniz formula for calculating the determinant of a matrix using upper and lower indexed arrays.
Demonstration of calculating the determinant of a 3x3 matrix using a step-by-step method.
Discussion of the skew symmetry property of the upper indexes in determinant calculations.
Introduction of the permutation symbol and its role in simplifying determinant calculations in tensor calculus.
Illustration of how to apply the permutation symbol to avoid hard-coded values in tensor expressions.
Explanation of the skew symmetry property of the permutation symbol in tensor calculus.
Development of a tensor calculus expression for the determinant that avoids hard-coded indexes.
Derivation of the final expression for the determinant using full contraction and permutation symbols.
Discussion on the practicality of using the derived tensor calculus expression for actual determinant calculations.
Inclusion of alternative index structures for determinants, such as two lower or two upper indexes.
Application of the determinant formula to different index structures while maintaining tensor calculus syntax.
Final summary emphasizing the importance of the correct index structure in tensor calculus determinant expressions.
Recap of the determinant calculation process using the Leibniz formula and permutation symbols.
Clarification on the use of permutation symbols to handle odd and even permutations in determinant calculations.
Conclusion highlighting the significance of the derived tensor calculus expressions for determinants in various index structures.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: