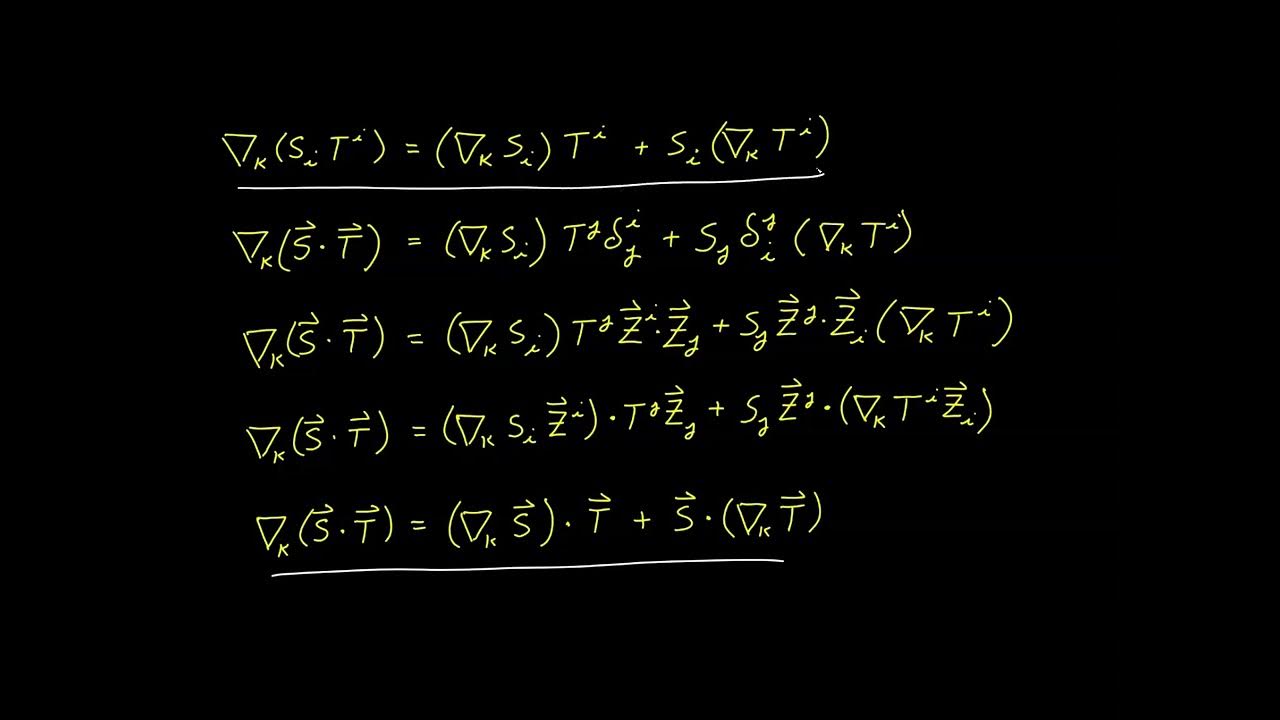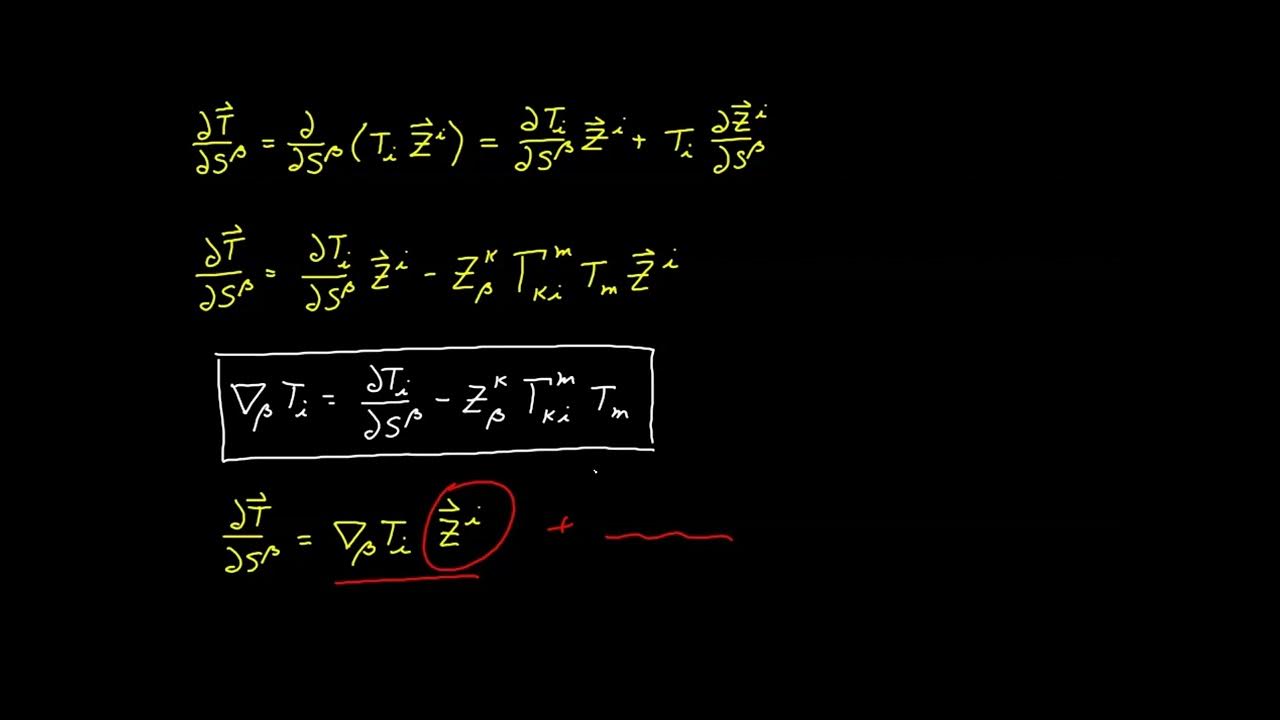Video 32 - Covariant Derivative for Covariant Vector

Tensor Calculus

4 Jun 202218:17

EducationalLearning

32 Likes 10 Comments

TLDRIn this educational video, the presenter delves into the intricacies of tensor calculus, specifically focusing on deriving the expression for the covariant derivative as it pertains to covariant vector components. They employ a contravariant basis vector and covariant components to explore the concept, applying the product rule to partial derivatives and introducing a new factor, pi, to represent the linear combination. The analysis reveals that pi is directly related to the Christoffel symbol, leading to a simplified expression for the covariant derivative. The video concludes with a comparison of the covariant and contravariant vector components' derivatives, highlighting their structural similarities and differences, and sets the stage for a proof of their tensorial nature in the next installment.

Takeaways

📚 The video is part of a series on tensor calculus, specifically focusing on the covariant derivative in relation to covariant vector components.
🔍 The script derives the expression for the covariant derivative of a covariant vector component, building upon the work done in a previous video on contravariant vector components.
📐 The process involves taking the partial derivative of a vector represented in a contravariant basis, using the product rule and considering the basis vector's partial derivative.
🧩 The script introduces a new factor, pi, to represent the linear combination resulting from the decomposition of the partial derivative of the basis vector.
🔄 The pi factor is shown to be not independent but directly related to the Christoffel symbol, simplifying the expression to involve negative gamma terms.
📉 The final expression for the covariant derivative of a covariant vector component is presented, highlighting the structure and significance of the Christoffel symbol.
🔄 The script contrasts the covariant derivative of covariant and contravariant vector components, noting the structural similarities and differences.
📈 The covariant derivative operation is characterized by the addition of a covariant index, which is consistent whether dealing with covariant or contravariant vectors.
📝 The importance of index placement in the Christoffel symbol and its contraction is emphasized for both covariant and contravariant cases.
🔢 The script explains the significance of the sign associated with the Christoffel symbol in the expressions, with a negative sign for covariant and a positive sign for contravariant derivatives.
🚀 The video concludes with a promise of a direct proof in the next video that both derived expressions for covariant and contravariant derivatives are indeed tensors.

Q & A

What was the focus of video 28 in this series?
-Video 28 focused on deriving the expression for the covariant derivative as it relates to contravariant vector components.
What is the main topic of discussion in video 32?
-Video 32 discusses the derivation of the expression for the covariant derivative as it relates to covariant vector components.
What is the difference between contravariant and covariant vectors in the context of covariant derivatives?
-Contravariant vectors have their indices in the upper position, while covariant vectors have their indices in the lower position. This affects how the covariant derivative is calculated and represented.
How is the product rule applied when taking the partial derivative of the vector in this context?
-The product rule is applied by first taking the partial derivative of the vector component while holding the basis vector fixed, then adding a term that multiplies the component by the partial derivative of the basis vector.
What role does the Christoffel symbol play in the derivation?
-The Christoffel symbol is used to form a linear combination when deriving the covariant derivative. It helps in relating the partial derivatives of the basis vectors to the overall expression.
What does the term 'linear combination' refer to in this derivation?
-A linear combination refers to the process of expressing a vector as a sum of other vectors, each multiplied by a scalar. In this derivation, it's used to decompose the partial derivatives of the basis vectors.
Why is it necessary to rename indices during the derivation process?
-Renaming indices ensures consistency and correctness in the mathematical expressions. It allows the terms to be aligned properly so that the final expression is coherent and meaningful.
How does the covariant derivative differ between covariant and contravariant vector components?
-For covariant vector components, the covariant derivative involves a subtraction of the Christoffel symbol term, while for contravariant components, it involves an addition. The positions of the indices also differ, affecting the final tensor form.
What is meant by 'mixed' tensors in this context?
-Mixed tensors refer to tensors that have both covariant and contravariant indices. For example, a tensor with one upper index and one lower index is a mixed tensor.
Why is the covariant derivative operation named as such?
-The covariant derivative operation is named because it adds a covariant index to the tensor being differentiated. This is true regardless of whether the original vector is covariant or contravariant.

Outlines

00:00

📚 Introduction to Covariant Derivative for Covariant Vector Components

This paragraph introduces the topic of deriving the covariant derivative for covariant vector components, following the approach from a previous video on contravariant vector components. The process involves taking the partial derivative with respect to a basis vector, applying the product rule, and decomposing the result into a linear combination. The focus is on understanding the relationship between the covariant derivative and the basis vectors, as well as the introduction of a new factor, pi, which is later related to the Christoffel symbol.

05:02

🔍 Exploring the Relationship with Christoffel Symbols

The second paragraph delves into the relationship between the newly introduced pi factor and the Christoffel symbols. By taking the partial derivative of the dot product of a basis vector with the contravariant basis and comparing it to the Christoffel symbol, it is revealed that pi is directly related to the negative of the Christoffel symbol. This realization simplifies the expression for the covariant derivative, eliminating the need for the pi factor and allowing the use of the Christoffel symbol directly in the linear combination.

10:05

📝 Deriving the Covariant Derivative Expression

In this paragraph, the process of deriving the covariant derivative expression for a covariant vector component is detailed. By renaming indices and factoring out common terms, the expression is simplified to a linear combination involving the partial derivative of the vector component and the Christoffel symbol. The result is a tensor expression that represents the covariant derivative with respect to a given index, showcasing the structure and significance of the covariant derivative in tensor calculus.

15:05

📚 Contrasting Covariant and Contravariant Derivatives

The final paragraph contrasts the derived expression for the covariant derivative of a covariant vector component with the previously derived expression for a contravariant vector component. It highlights the structural similarities and differences, such as the placement of indices and the sign of the Christoffel symbol term. The paragraph also explains the importance of the covariant derivative in tensor calculus, emphasizing its role in adding a covariant index and the implications for tensor rank and type.

Mindmap

Keywords

💡Tensor

A tensor is a mathematical object that generalizes scalars, vectors, and matrices to describe quantities with more complex transformations. In the context of the video, tensors are used to represent physical quantities in a way that is invariant under changes in the coordinate system. The video discusses the covariant derivative of tensors, which is a key concept in differential geometry and general relativity.

💡Covariant Derivative

The covariant derivative is a differential operator that generalizes the directional derivative to curved spaces. It is used to take derivatives of tensors in a way that is consistent with the curvature of the space. In the video, the covariant derivative is derived for both contravariant and covariant vector components, showing how it can be calculated and what it represents in the context of tensor calculus.

💡Contravariant Vector

A contravariant vector is a type of vector in a vector space that transforms in the opposite way to the basis vectors under a change of coordinates. In the script, the covariant derivative is initially derived for contravariant vector components, which is a foundational step before moving on to covariant vector components.

💡Covariant Vector

A covariant vector is a vector that transforms in the same way as the basis vectors under a change of coordinates. The video script discusses deriving the expression for the covariant derivative as it relates to covariant vector components, which is essential for understanding how these vectors behave under transformations.

💡Christoffel Symbol

The Christoffel symbol is a function that encodes the curvature of a manifold and is used in the computation of the covariant derivative. In the video, the Christoffel symbol is related to the new factor introduced, which is later identified as being directly related to the negative of the Christoffel symbol itself.

💡Partial Derivative

A partial derivative is the derivative of a function with respect to one variable, while the other variables are held constant. In the video, partial derivatives are taken with respect to different coordinates to derive the covariant derivative expressions for both contravariant and covariant vector components.

💡Product Rule

The product rule is a fundamental calculus rule that states how to differentiate a product of two functions. In the script, the product rule is used when taking the partial derivative of the basis vector components with respect to a coordinate, which is a step in deriving the covariant derivative.

💡Linear Combination

A linear combination is an expression constructed from a set of vectors by multiplying each vector by a scalar and adding the results. In the video, the covariant derivative is expressed as a linear combination of basis vectors, which is a common technique in tensor calculus to simplify expressions.

💡Covariance and Contrariance

Covariance and contrariance refer to how quantities transform under changes in the coordinate system. Covariant quantities transform like the basis vectors, while contravariant quantities transform in the opposite way. The video script discusses the covariant derivative for both covariant and contravariant vector components, highlighting the importance of these concepts in tensor calculus.

💡Second-Rank Tensor

A second-rank tensor is a tensor with two indices, which can be thought of as a matrix. In the video, the covariant derivative of a covariant vector component is shown to be a second-rank tensor, indicating that it has two indices and can be represented as a matrix.

💡Quotient Theorem

The quotient theorem in tensor calculus is used to determine whether a given expression is a tensor. In the video, the quotient theorem is implicitly referred to when concluding that the derived expression for the covariant derivative of a covariant vector component is indeed a tensor.

Highlights

Introduction to deriving the expression for the covariant derivative as it relates to covariant vector components.

Using a contravariant basis to represent the vector T and the necessity of a covariant component with a contravariant basis.

Application of the product rule to take the partial derivative of both sides with respect to zj.

Decomposition of the partial derivative of a vector into a linear combination with two free indexes.

Introduction of the letter pi to represent the linear factor in the decomposition.

Dot product of both sides with respect to the covariant basis vector zm.

Simplification to pi i j k with the use of the Kronecker delta term.

Switching sides of the equation and renaming the index m back to k.

Derivation of the expression for the covariant derivative using the Christoffel symbol.

Identification of pi i j k as being directly related to the Christoffel symbol.

Substitution of the derived expression back into the original line of investigation.

Renaming of indexes in the second term for consistency with the first term.

Final expression for the covariant derivative of a covariant vector component.

Explanation of the difference between the covariant and contravariant vector components' covariant derivatives.

Discussion on the structure of contractions in the covariant derivative expressions.

Clarification on the naming convention and the technical correctness of referring to covariant vector components as covariant vectors.

Summary of the ability to take the covariant derivative of either a covariant or contravariant vector component.

Teaser for the next video, which will provide a direct proof that both expressions are indeed tensors.

Transcripts

Browse More Related Video

Video 28 - Covariant Derivative for Contravariant Vector

Video 33 - Covariant Derivative Proof

Video 37 - Metrinilic Property - Part 1

Video 72 - Surface Covariant Derivative for Non Tangent Vectors

Video 17 - Contravariant Basis

Video 27 - Transformation of Partial Derivatives