Standard Error of the Mean: Concept and Formula | Statistics Tutorial #6 | MarinStatsLectures

MarinStatsLectures-R Programming & Statistics
8 Aug 201805:25
EducationalLearning
32 Likes 10 Comments

TLDRThe video script delves into the concept of standard deviation and standard error in the context of sample means. It explains why the standard deviation of a sample mean is referred to as the standard error, and how it is calculated as the population standard deviation divided by the square root of the sample size (n). The explanation is grounded in properties of variance, such as the impact of constants on variance and the sum of variances for independent variables. The script clarifies that when dealing with a random, independent sample, the variance of the sample mean simplifies to the population variance divided by the sample size, leading to the standard deviation of the sample mean being the population standard deviation divided by the square root of the sample size.

Takeaways
  • πŸ“ˆ The standard deviation of the sample mean is often referred to as the standard error of the sample mean.
  • πŸ”’ The formula for the standard error is the population standard deviation (Οƒ) divided by the square root of the sample size (n).
  • 🌐 The standard deviation of a constant times a variable (aX) is equal to the constant squared times the variance of the variable (a^2 * Var(X)).
  • βž• The variance of the sum of two independent variables (x1 + x2) is equal to the sum of their individual variances (Var(x1) + Var(x2)).
  • πŸ”„ When calculating the variance of the sample mean, each individual observation's variance is assumed to be the same (Οƒ^2).
  • πŸ“Š The variance of the sample mean is calculated by dividing the sum of the variances of individual observations by the sample size (n).
  • 🌟 Since the observations in a random sample are assumed to be independent, their variances can be summed directly.
  • πŸ“‰ The standard deviation of the sample mean (ΟƒXΜ„) is the square root of the variance of the sample mean (Οƒ^2 / n).
  • πŸ“Œ In practice, the population standard deviation (Οƒ) is often replaced with the sample standard deviation when working with sample data.
  • πŸ”„ The process of deriving the standard error involves step-by-step application of variance properties and assumptions about the sample data.
  • πŸ“ˆ Understanding the standard error is crucial for making inferences about population parameters from sample data.
Q & A

  • Why is the standard deviation of the sample mean referred to as the standard error of the sample mean?

    -The standard deviation of the sample mean is called the standard error because it measures the average amount of error or deviation from the true population mean that we would expect if we were to take multiple samples of size n from the same population. It is an estimate of the precision of the sample mean as an estimator of the population mean.

  • What is the relationship between the standard deviation of individual observations and the standard deviation of the sample mean?

    -The standard deviation of the sample mean (standard error) is equal to the standard deviation of the individual observations (Sigma) divided by the square root of the sample size (n). This relationship is derived from the properties of variance and the assumption that the observations are independent.

  • What are the two properties used to derive the formula for the standard deviation of the sample mean?

    -The two properties used are: (1) the variance of a constant times a random variable is equal to the constant squared times the variance of the random variable, and (2) the variance of the sum of two independent random variables is equal to the sum of their individual variances.

  • How does the variance of the sample mean relate to the variance of the individual observations in a sample?

    -The variance of the sample mean is the sum of the variances of the individual observations divided by the square of the sample size (n). Since all observations in a random sample are assumed to have the same variance (Sigma squared), the variance of the sample mean is n times Sigma squared divided by n, which simplifies to Sigma squared divided by n.

  • What is the assumption made about the observations in a random sample when calculating the standard deviation of the sample mean?

    -The assumption is that all observations in the random sample have the same mean and variance, and that the observations are independent of each other.

  • What does the formula Sigma over the square root of n represent?

    -The formula Sigma over the square root of n represents the standard deviation of the sample mean, also known as the standard error of the sample mean, which is used to estimate the precision of the sample mean as an estimator of the population mean.

  • How does the standard error of the sample mean change as the sample size increases?

    -As the sample size (n) increases, the standard error of the sample mean decreases, which means that the sample mean becomes a more precise estimator of the population mean.

  • What is the significance of the standard error in statistical inference?

    -The standard error is significant in statistical inference because it provides a measure of the variability of the sample mean and helps in constructing confidence intervals and conducting hypothesis tests about the population mean.

  • In the context of the script, what does Sigma represent?

    -In the context of the script, Sigma represents the standard deviation of the individual observations in the sample, which is a measure of the dispersion or variability of those observations.

  • How does the concept of independence affect the calculation of the variance of the sample mean?

    -The concept of independence is crucial because it allows us to assume that the variances of the individual observations can be added together when calculating the variance of the sample mean. If the observations were not independent, we could not simply sum their variances.

  • What happens to the precision of the sample mean if we assume the observations are not independent?

    -If the observations are not independent, we cannot use the simplifying assumption that allows us to sum their variances directly. This would mean that the calculations for the variance of the sample mean and its standard error would be more complex, and the precision of the sample mean as an estimator might not be accurately reflected.

Outlines
00:00
πŸ“Š Understanding the Standard Error of the Sample Mean

This paragraph delves into the concept of standard deviation in the context of sample means. It explains why the standard deviation of a sample mean is referred to as the standard error. The discussion begins with the foundational properties of variance, including the impact of constants on variance and the sum of variances for independent variables. The explanation progresses to describe how the variance of the sample mean (X bar) is derived, emphasizing the role of the sample size (n) and the population standard deviation (Sigma). The paragraph concludes with the derivation of the formula for the standard error, which is Sigma over the square root of n, highlighting the transition from population to sample statistics in statistical analysis.

05:01
🚫 Incomplete Paragraph - Missing Context

The second paragraph appears to be incomplete and lacks context. It starts with an abrupt sentence that seems unrelated to the statistical discussion from the first paragraph. The content provided is insufficient for a detailed summary, as it does not offer a clear theme or sufficient information to understand the intended message.

Mindmap
Keywords
πŸ’‘Standard Deviation
Standard deviation is a measure of the amount of variation or dispersion of a set of values. In the context of the video, it refers specifically to the variability within individual observations in a dataset or distribution. The standard deviation of the sample mean, also known as the standard error, is discussed as being equal to the population standard deviation (Sigma) divided by the square root of the sample size (n). This concept is crucial for understanding how variability in a dataset is quantified and how it decreases as sample size increases.
πŸ’‘Sample Mean
The sample mean (X-bar) is the average of all the numeric values in a sample. It is a central measure of location for the data points. The video explores how to calculate the variance of the sample mean as a step towards understanding its standard deviation. By taking the mean of a sample, we obtain a single value that best represents the central tendency of the data, and this process is pivotal for statistical analysis in sample data.
πŸ’‘Variance
Variance measures how far a set of numbers is spread out. The video demonstrates the use of variance in calculating the standard error of the sample mean. Specifically, it explains properties of variance, such as how it changes when all values in a dataset are multiplied by a constant, and how the variance of a sum of independent variables can be found by summing their variances. This foundational concept is essential for understanding the dispersion within a dataset.
πŸ’‘Sigma
Sigma (Οƒ) represents the population standard deviation in statistics, a measure of the dispersion or variability within a population dataset. The video explains how Sigma is used in the formula for the standard deviation of the sample mean, emphasizing its role in measuring variability across the population from which samples are drawn. Sigma squared (Οƒ^2) is used to denote population variance.
πŸ’‘Square Root of n
The square root of n, where n is the sample size, is a crucial component in the formula for calculating the standard error of the sample mean. It represents the factor by which the population standard deviation (Sigma) is divided to obtain the standard deviation of the sample mean. This concept highlights the inverse relationship between sample size and the standard error, illustrating how increasing the sample size reduces the variability of the sample mean.
πŸ’‘Standard Error
Standard error of the sample mean is the standard deviation of the sampling distribution of the sample mean. It quantifies how much the sample mean varies from the true population mean. The video clarifies that the standard error decreases as the sample size increases, due to the formula involving division by the square root of n. This concept is fundamental in inferential statistics for estimating the precision of sample estimates.
πŸ’‘Independent Random Sample
An independent random sample is a set of individuals or observations drawn from a population where each member has an equal chance of being selected, and the selection of one member does not influence the selection of another. The video assumes that the observations in the sample are independent, which justifies the addition of variances when calculating the variance of the sample mean. This assumption is critical for the mathematical properties of variance to hold true in the context of sampling.
πŸ’‘Population
In statistics, a population refers to the entire group that is the subject of a study. The video contrasts population parameters, such as the population mean and standard deviation (Sigma), with sample statistics like the sample mean and standard error. Understanding the difference between population and sample is essential for applying statistical methods correctly in research.
πŸ’‘Sample Size
Sample size (n) refers to the number of observations or data points in a sample. It plays a significant role in determining the standard error of the sample mean, as seen in the formula where Sigma is divided by the square root of n. The video emphasizes the impact of sample size on statistical precision, showing that a larger sample size leads to a smaller standard error and thus more reliable estimates of population parameters.
πŸ’‘Properties of Variance
The video discusses two key properties of variance that are foundational to understanding statistical analysis: 1) The variance of a constant times a variable is equal to the constant squared times the variance of the variable. 2) The variance of the sum of two independent variables is the sum of their variances. These properties are essential for deriving the formula for the standard error of the sample mean and for understanding the behavior of variance in different statistical scenarios.
Highlights

The standard deviation of the sample mean is referred to as the standard error of the sample mean.

The standard deviation of the sample mean is calculated as Sigma over the square root of n, where Sigma is the standard deviation of the population.

The variance of a constant times a random variable is equal to the constant squared times the variance of the random variable.

The variance of the sum of two independent random variables is equal to the sum of their individual variances.

The sample mean is calculated by dividing the sum of the sample data points by the sample size.

The variance of the sample mean is found by dividing the variance of each individual data point by the square of the sample size.

The assumption is made that each data point in the sample has the same mean and variance, indicating that the sample is randomly drawn from the population.

The process starts by working with the variance of the sample mean, which is expressed as the variance of the sum of the data points divided by the sample size.

The constant (1/n) is factored out of the variance when working with the sample mean, which simplifies the expression.

Since the sample data points are assumed to be independent, the variance of their sum can be expressed as the sum of their individual variances.

Each observation in the sample has the same variance, denoted as Sigma squared, which is the standard deviation squared.

The variance of the sample mean is calculated as Sigma squared divided by the sample size (n).

The standard deviation of the sample mean, or standard error, is the square root of the variance of the sample mean.

The standard error is used when dealing with sample data instead of population data, and it is represented by the sample standard deviation.

The derivation of the standard error formula demonstrates the relationship between the sample size and the precision of the estimate of the population mean.

The standard error decreases as the sample size increases, leading to a more precise estimate of the population mean.

Transcripts

Browse More Related Video

Standard error of the mean | Inferential statistics | Probability and Statistics | Khan Academy

Sample standard deviation and bias | Probability and Statistics | Khan Academy

Why do we divide by n-1 and not n? | shown with a simple example | variance and sd

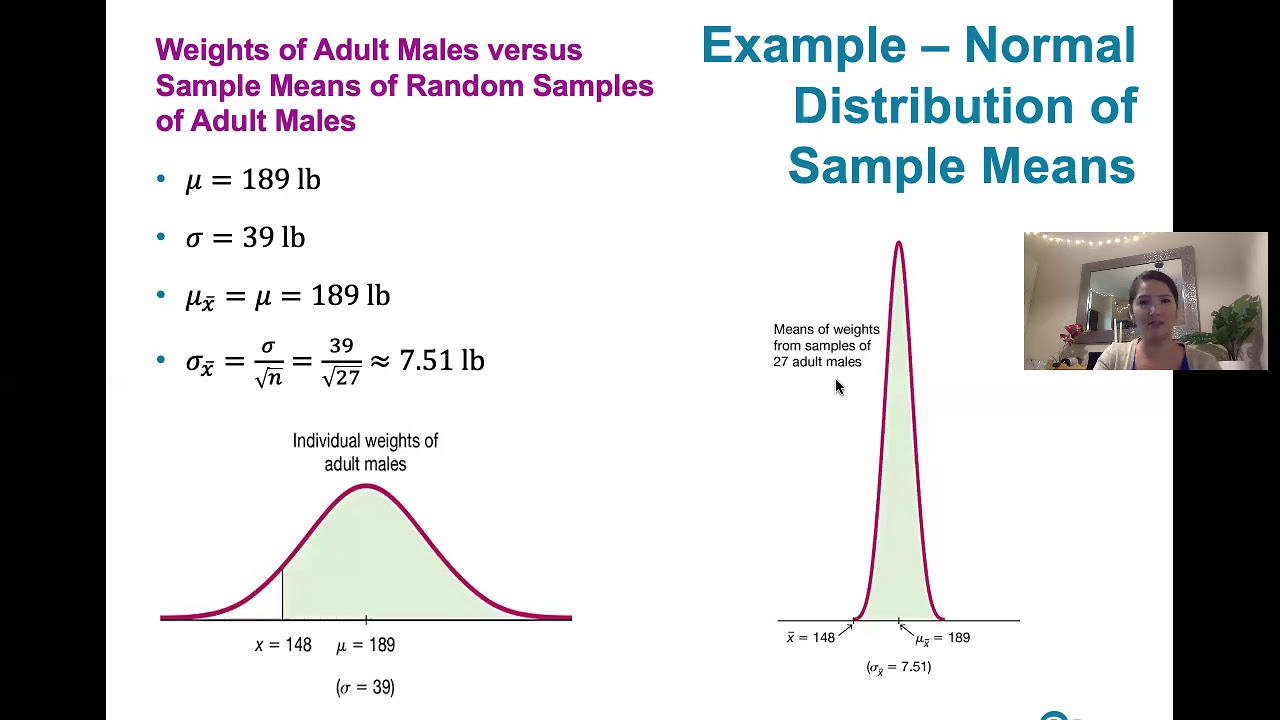
6.4.1 The Central Limit Theorem - What the Central Limit Theorem Says and What It Doesn't Say

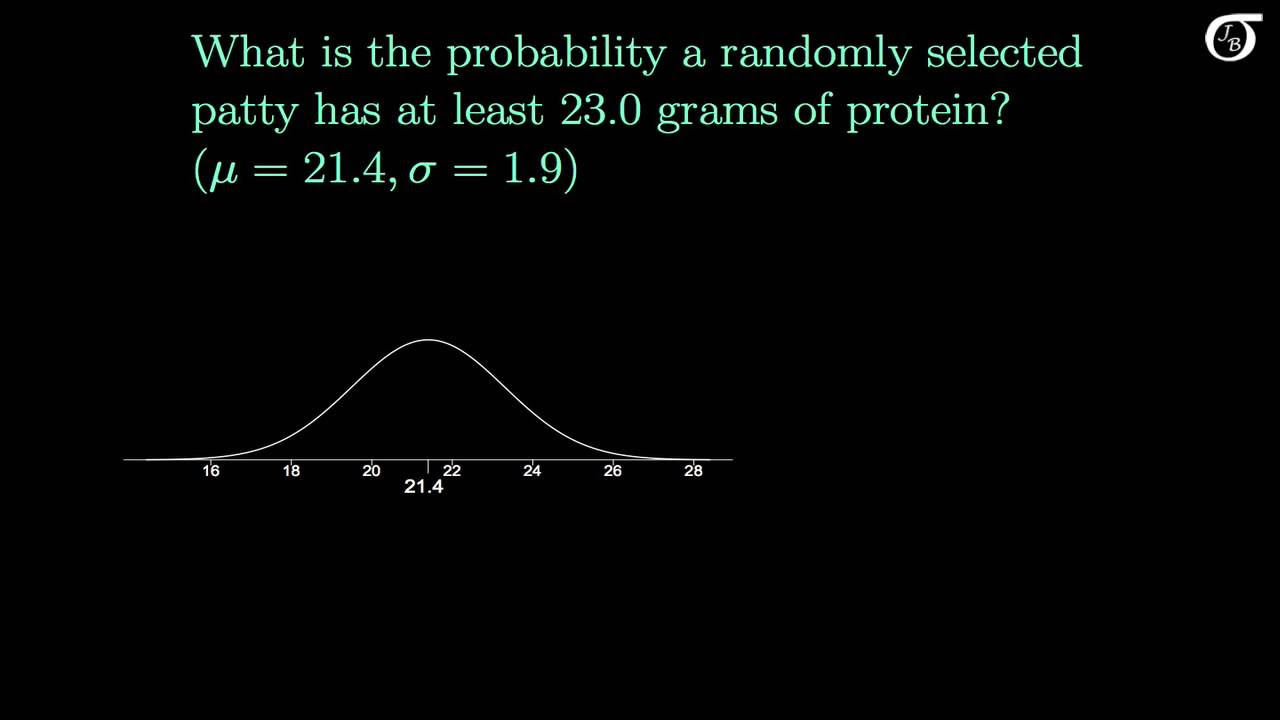
The Sampling Distribution of the Sample Mean

Variance and Standard Deviation: Sample and Population Practice Statistics Problems

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
StatisticsStandard DeviationVariance PropertiesSample MeanStandard ErrorMathematical ConceptsEducational ContentProbability TheoryData AnalysisRandom Sampling