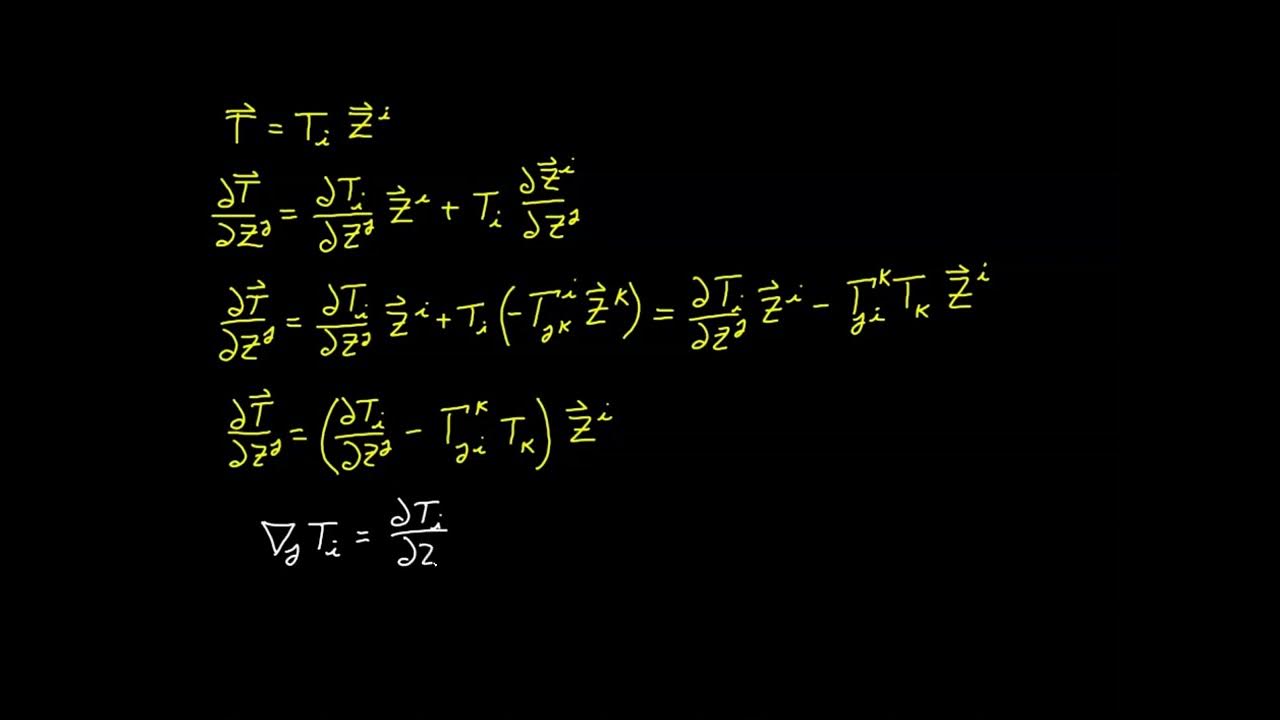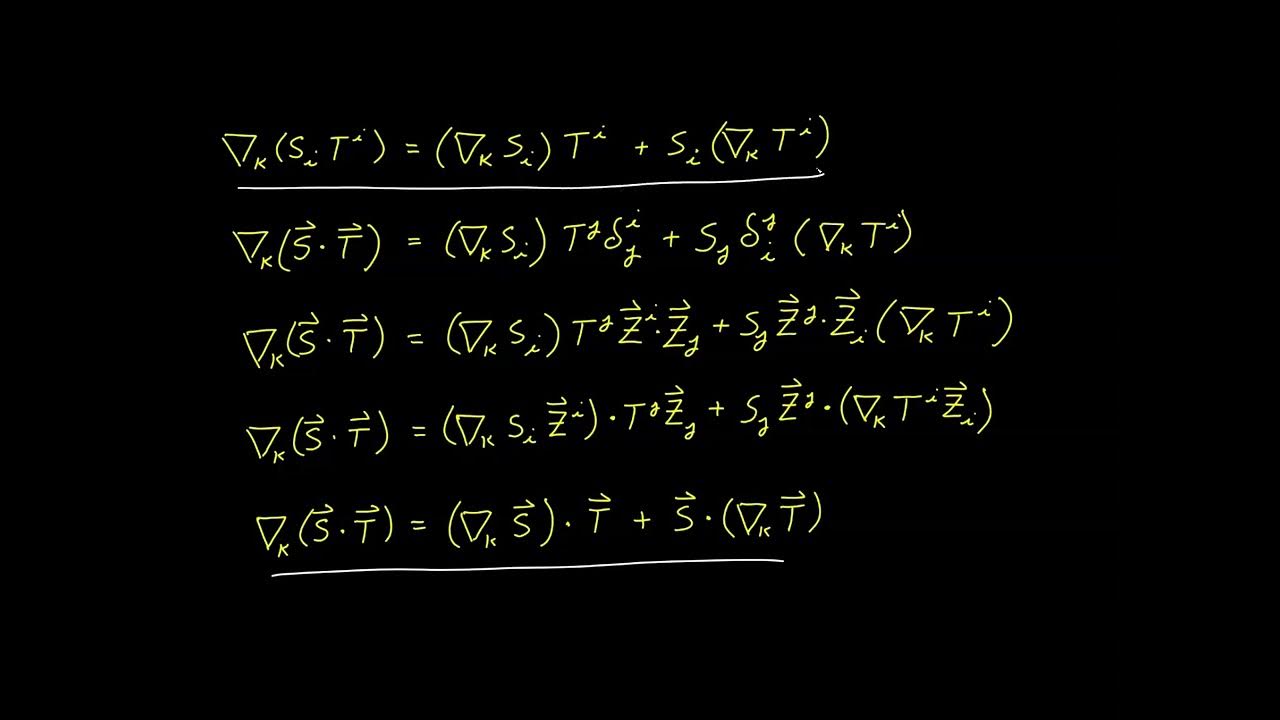Video 28 - Covariant Derivative for Contravariant Vector

Tensor Calculus

4 Jun 202220:55

EducationalLearning

32 Likes 10 Comments

TLDRThis video introduces the covariant derivative in tensor calculus, a crucial operator for contravariant vector components that resolves issues with partial derivatives. The script explains the need for the covariant derivative due to non-constant basis vectors and defines the Christoffel symbol, highlighting its symmetry and zero value in affine coordinates. The covariant derivative is presented as a tensor operation, equivalent to partial derivatives in affine coordinates, and is identified as the correct expression for divergence, making it a fundamental tool for tensor calculus.

Takeaways

🔍 The video introduces a new operator called the covariant derivative, which is used to address issues with partial derivatives in tensor calculus.
📚 The covariant derivative is defined in relation to contravariant vector components and is used to rectify issues encountered with partial derivatives in the previous video.
📉 The script explains that in tensor calculus, basis vectors are not constant, necessitating the use of the product rule when taking partial derivatives.
📌 The partial derivative of a basis vector introduces a new factor, leading to the definition of the covariant derivative and the Christoffel symbol.
📝 The Christoffel symbol, denoted by \( \Gamma^k_{ij} \), is a scalar factor used to represent the partial derivative of a basis vector as a linear combination of other basis vectors.
🔄 The Christoffel symbol has the property of being symmetric in its lower indices, meaning \( \Gamma^k_{ij} = \Gamma^k_{ji} \).
🗜 In affine coordinates, where basis vectors are constant, the Christoffel symbol is zero, simplifying the expressions involving it.
🔄 The covariant derivative is a tensor, which means it has the necessary properties to be used in various tensor operations, unlike the partial derivative.
📈 The covariant derivative provides a solution to the problem of divergence in tensor calculus, offering a tensorial expression for the divergence of a vector field.
🔧 The script demonstrates that the covariant derivative can be used to generalize partial derivatives in tensor calculus, making them applicable in all coordinate systems, not just affine ones.
🚀 The video concludes by highlighting the broader applications of the covariant derivative in tensor calculus, including its use in gradient, laplacian, and curl operations.

Q & A

What is the main topic of the video?
-The main topic of the video is the introduction of the covariant derivative in tensor calculus, specifically as it relates to contravariant vector components.
Why is the covariant derivative necessary?
-The covariant derivative is necessary to rectify issues encountered with partial derivatives in tensor calculus, particularly when dealing with non-constant basis vectors.
What is the relationship between the covariant derivative and partial derivatives?
-The covariant derivative can be thought of as a generalized partial derivative that produces a tensor, unlike the partial derivative of a component which is not a tensor.
What is the significance of the basis vectors in tensor calculus?
-In tensor calculus, basis vectors are not constant in general, which means the product rule must be used when taking their partial derivatives, introducing additional complexity compared to affine coordinates.
What is the Christoffel symbol and why is it important?
-The Christoffel symbol is a scalar factor used to represent the partial derivative of a basis vector with respect to another basis vector as a linear combination of the basis vectors. It is important because it helps define the covariant derivative and has properties that are key to tensor calculus.
What property does the Christoffel symbol have regarding its indexes?
-The Christoffel symbol is symmetric in its lower indexes, meaning that swapping the two lower indexes does not change the value of the symbol.
How is the covariant derivative defined for a contravariant vector component?
-The covariant derivative for a contravariant vector component is defined as a linear combination involving the partial derivative of the vector component, the Christoffel symbol, and the basis vectors.
What is the significance of the covariant derivative in the context of divergence?
-The covariant derivative provides the correct expression for the divergence in tensor calculus, as it is a tensor and gives the correct results in all coordinate systems, including Cartesian coordinates.
How does the covariant derivative differ when dealing with covariant objects?
-While the covariant derivative for a contravariant vector component has been discussed, the expression varies slightly when dealing with covariant objects, which is a subject for further exploration in another video.
What broader applications does the covariant derivative have in tensor calculus?
-The covariant derivative has broader applications in tensor calculus, particularly in operations involving partial differentiation such as gradient, Laplacian, and curl, where it replaces the partial derivative to maintain tensor properties.

Outlines

00:00

📚 Introduction to Covariant Derivative

This paragraph introduces the covariant derivative, a new operator in tensor calculus, which addresses issues with partial derivatives when dealing with contravariant vector components. The covariant derivative is defined through the partial derivative of a vector represented as a linear combination in the covariant basis. The explanation includes the use of the product rule due to the non-constant nature of basis vectors in tensor calculus, leading to the introduction of the concept of taking the partial derivative of a basis vector, which was previously unexplored.

05:01

🔍 Exploring the Basis Vector's Derivative

The script delves into the derivative of the basis vector, explaining its definition as the partial derivative of the position vector with respect to a coordinate. It highlights that this derivative introduces a covariant index, leading to three expressions instead of one. The paragraph further explores the implications of taking a second derivative, which results in nine expressions due to the introduction of another covariant index, emphasizing the symmetry of these expressions and their equivalence to the second derivative of the position vector in any order.

10:01

📈 The Christoffel Symbol and its Properties

The Christoffel symbol is introduced as the scalar factor in the linear combination representing the derivative of a basis vector. The paragraph discusses the properties of the Christoffel symbol, including its symmetry in its lower indexes and its value being zero for affine coordinates. The symbol is recognized as a crucial object in tensor calculus, with several upcoming videos dedicated to exploring its characteristics, transformations, and applications.

15:03

🌐 Redefining Partial Derivatives with Covariant Derivatives

The paragraph demonstrates the process of reorganizing the expression for the partial derivative of a vector into a linear combination involving the Christoffel symbol and the basis vectors. This leads to the definition of the covariant derivative, a new operation that rectifies the issue of partial derivatives not being tensors. The covariant derivative is shown to have two important properties: it always results in a tensor and equals the partial derivative in affine coordinates, thus solving the divergence problem encountered in the previous video.

20:04

📝 Correct Expression for Divergence and Future Exploration

The paragraph concludes with the correct expression for the divergence using the covariant derivative, which is a tensor and yields accurate results in Cartesian coordinates. It emphasizes the broader applications of the covariant derivative in tensor calculus, especially in operations involving partial derivatives like gradient, Laplacian, and curl. The video script ends with a promise of a more in-depth analysis of the Christoffel symbol in subsequent videos.

Mindmap

Keywords

💡Covariant Derivative

The covariant derivative is a fundamental concept in differential geometry and tensor calculus, which generalizes the notion of the derivative to curved spaces. In the video, it is introduced as a new operator that addresses issues with partial derivatives when dealing with contravariant vector components. It is defined in such a way that it produces a tensor, which is crucial for maintaining the tensorial properties of operations in curved spaces. The video script illustrates its definition through the manipulation of basis vectors and their derivatives.

💡Contravariant Vector

A contravariant vector is a type of vector in tensor calculus that transforms in the opposite way to the basis vectors of a coordinate system. In the context of the video, the covariant derivative is specifically defined for contravariant vector components, which is essential for the correct formulation of differential operations in non-Euclidean geometries. The script explains how the covariant derivative of a contravariant vector is calculated, which is key to understanding tensor operations in curved spaces.

💡Partial Derivative

A partial derivative is a derivative of a function with respect to one variable, while the other variables are held constant. In the script, the partial derivative is initially used to differentiate a vector expression but is found to be insufficient in tensor calculus due to its inability to handle the non-constant nature of basis vectors in curved spaces. The covariant derivative is then introduced as a solution to this problem.

💡Basis Vector

A basis vector is a vector that, along with others, forms a basis for a vector space. In the video, basis vectors are not constant and their derivatives play a crucial role in the definition of the covariant derivative. The script discusses how the partial derivative of a basis vector introduces additional terms in the differentiation process, necessitating the use of the product rule.

💡Christoffel Symbol

The Christoffel symbol is a function that encodes the curvature of a manifold and is used in the definition of the covariant derivative. In the video, it is defined as the scalar factor in the linear combination that represents the derivative of a basis vector with respect to another basis vector. The script explains that the Christoffel symbol has properties of symmetry in its lower indices and is zero for affine coordinates.

💡Tensor

A tensor is a mathematical object that generalizes scalars, vectors, and other quantities in a way that is invariant under coordinate transformations. In the video, the covariant derivative is shown to always produce a tensor, which is essential for maintaining the correct transformation properties under changes of coordinates. The script emphasizes the importance of tensors in differential geometry and their role in the covariant derivative.

💡Divergence

Divergence is a measure of how a vector field spreads out or converges at a given point. In the script, the divergence of a vector field is discussed in the context of tensor calculus, where it is shown that the covariant derivative provides the correct expression for divergence, unlike the partial derivative, which does not yield a tensor.

💡Affine Coordinates

Affine coordinates are a type of coordinate system where the basis vectors are constant. The script mentions that in affine coordinates, the Christoffel symbols are zero, which simplifies the covariant derivative to the standard partial derivative. This is important because it shows that the covariant derivative generalizes the partial derivative to non-Euclidean spaces.

💡Product Rule

The product rule is a fundamental principle in calculus that states how to differentiate a product of two functions. In the video, the product rule is applied when differentiating a vector with respect to a coordinate, leading to the introduction of the Christoffel symbol and the covariant derivative.

💡Symmetric Matrix

A symmetric matrix is a matrix that is equal to its transpose, meaning that its elements are the same when the row and column indices are swapped. In the script, the covariant derivatives of basis vectors form such a matrix, which is symmetric due to the interchangeability of the indices i and j in the second derivative of the position vector.

💡Linear Combination

A linear combination is an expression constructed from a set of terms by multiplying each term by a scalar factor and adding the results. In the video, the covariant derivative is expressed as a linear combination of basis vectors and scalar factors, which is a key step in defining the operation and showing its tensorial nature.

Highlights

Introduction of the covariant derivative, a new operator for contravariant vector components.

Explanation of issues with partial derivatives in tensor calculus and how the covariant derivative rectifies them.

Representation of a vector T as a linear combination using a covariant basis.

Use of the product rule to differentiate a vector with respect to a basis vector.

Introduction of the concept of basis vectors not being constant in tensor calculus.

Definition of the basis vector z_i as the partial derivative of the position vector with respect to z_i.

Discussion on the covariant index and its role in defining three vectors simultaneously.

Introduction of the second covariant index and the expansion to nine expressions.

Explanation of the symmetry in the second derivatives of the position vector.

Introduction of the concept of a symmetric matrix in the context of tensor calculus.

Representation of the partial derivative of z_i with respect to z_j as a vector.

Introduction of the linear combination representation for the partial derivative of basis vectors.

Definition and explanation of the Christoffel symbol of the second kind.

Properties of the Christoffel symbol, including its symmetry in the lower indexes.

Condition under which the Christoffel symbol equals zero, specifically in affine coordinates.

Derivation of the covariant derivative for a contravariant vector component.

Explanation of the covariant derivative as a tensor operation, with properties and practical applications.

Identification of the covariant derivative as the correct expression for the divergence in tensor calculus.

Discussion on the broader application of the covariant derivative in tensor calculus beyond divergence.

Conclusion summarizing the significance of the covariant derivative and its properties.

Transcripts

Browse More Related Video

Video 32 - Covariant Derivative for Covariant Vector

Video 27 - Transformation of Partial Derivatives

Tensor Calculus Lecture 6c: The Covariant Derivative 2

Video 37 - Metrinilic Property - Part 1

Video 31 - Christoffel Symbol Examples

Video 74 - Weingarten's Formula

Related Tags

Tensor Calculus Covariant Derivative Vector Analysis Christoffel Symbol Partial Derivative Affine Coordinates Divergence General Relativity Mathematical Physics Differential Geometry