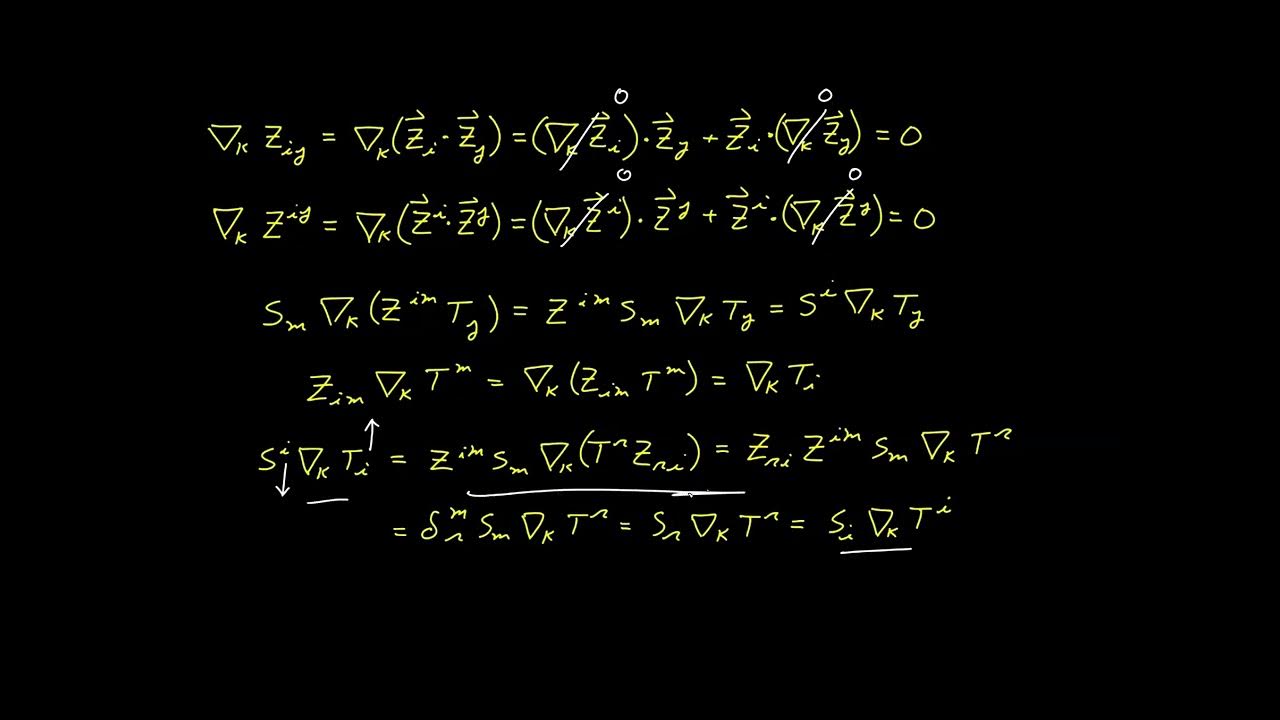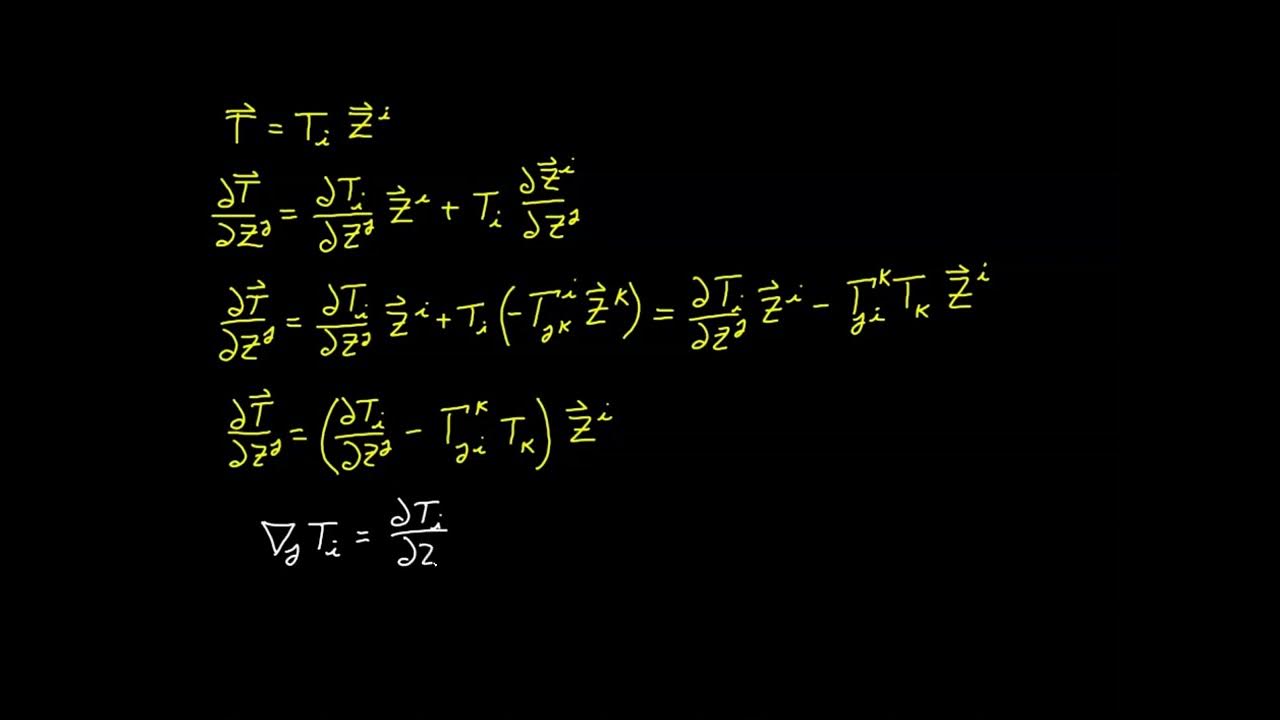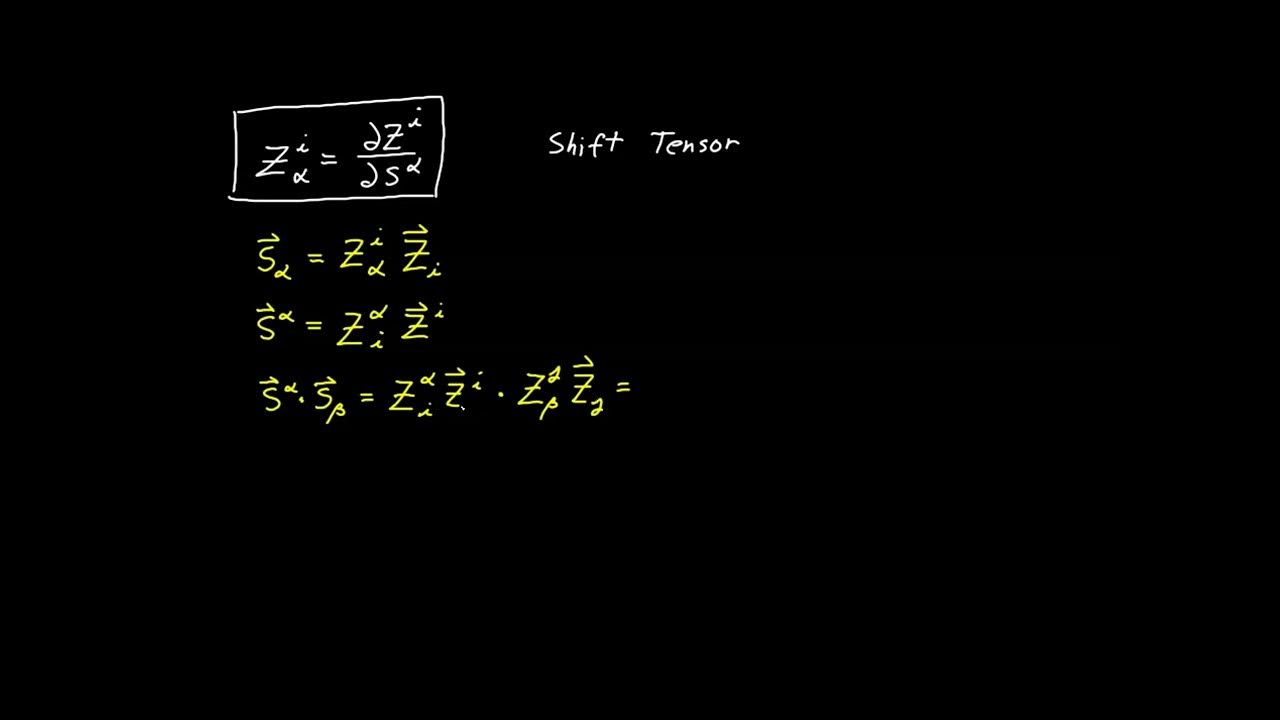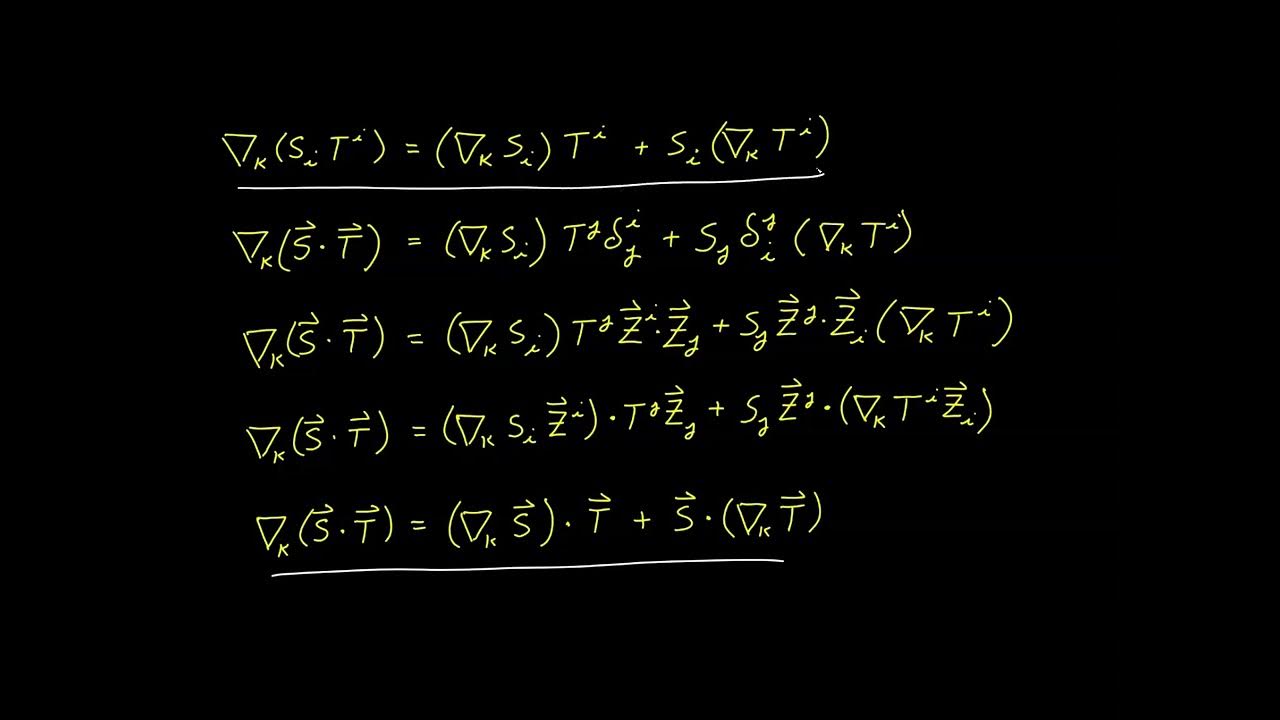Video 27 - Transformation of Partial Derivatives
TLDRIn this 27th installment of the tensor calculus series, the focus is on deriving transformation equations for partial derivatives, essential for developing advanced calculus expressions involving these derivatives. The video explores the concept of divergence in Cartesian coordinates, its physical interpretations as a sink or source, and its applications in fluid dynamics, electromagnetism, and gravitation. The attempt to express divergence as a tensor equation is discussed, revealing that while the partial derivative of a scalar function transforms as a tensor, those of vector components, both covariant and contravariant, do not. This insight is crucial for understanding the limitations in tensor calculus when dealing with vector fields.
Takeaways
- 📚 The video is part of a series on tensor calculus, focusing on deriving transformation equations for partial derivatives.
- 🌐 The divergence is introduced as a scalar function that measures the increase or decrease of a quantity represented by a vector field.
- 💧 The concept of divergence is related to inflow and outflow, where a negative divergence indicates a 'sink' and a positive one indicates a 'source'.
- 🚀 Divergence has applications in fluid dynamics, electricity, magnetism, and gravitation, particularly in measuring the flow of incompressible fluids.
- 🔍 The goal is to express the divergence in tensor calculus to make it invariant across all coordinate systems.
- 🔢 The script discusses the transformation of tensor components in Cartesian coordinates using indexes for x, y, and z.
- 📉 The video highlights the problem of expressing the divergence as a tensor equation due to the presence of covariant and contravariant components.
- 🔄 The transformation equation for a partial derivative of a contravariant vector component is derived, revealing it does not transform as a tensor due to additional terms.
- 📈 Similarly, the partial derivative of a covariant vector component is shown not to transform as a tensor for the same reason.
- 🎓 The partial derivative of a scalar function is confirmed to transform as a tensor, a key result in tensor calculus.
- 🔑 The script concludes that while scalar function derivatives are tensors, vector component derivatives are not, indicating a challenge for expressions involving these derivatives.
Q & A
What is the main goal of the video?
-The main goal of the video is to derive transformation equations for partial derivatives in the context of tensor calculus, with the ultimate aim of developing an invariant tensor equation for the divergence that is valid for all coordinate systems.
What is the divergence in the context of vector calculus?
-The divergence is a scalar function that measures the increase or decrease of a quantity represented by a vector field at a given point in space. It can be thought of as the net inflow or outflow of the vector field through an infinitesimal volume of space.
Why is the divergence important in fluid dynamics?
-In fluid dynamics, the divergence is important because it measures the flow of an incompressible fluid. If the divergence is zero at any given point, it indicates that the flow into and out of that point is balanced, which is a characteristic of incompressible fluids.
What is the significance of expressing the divergence as a tensor equation?
-Expressing the divergence as a tensor equation allows for an invariant expression that is valid across all coordinate systems. This is crucial for generalizing the concept of divergence in different mathematical and physical contexts.
What is the difference between covariant and contravariant components in tensor calculus?
-Covariant components transform using a covariant transformation rule, while contravariant components transform using a contravariant transformation rule. The distinction is important for understanding how different types of tensors behave under changes of coordinates.
Why is the partial derivative of a vector component not a tensor?
-The partial derivative of a vector component is not a tensor because its transformation equation includes additional terms that do not fit the required tensor transformation pattern. This means it does not transform as a tensor under coordinate changes.
What is the Jacobian matrix and how is it used in the video?
-The Jacobian matrix is a matrix of all first-order partial derivatives of a vector-valued function. In the video, it is used to express the transformation between different coordinate systems and to derive the transformation equation for partial derivatives.
What is the chain rule used for in the context of this video?
-The chain rule is used to take the derivative of a function of another function, which is necessary when transforming the partial derivatives of tensor components from one coordinate system to another.
What does it mean for an expression to be 'fully contracted' in tensor calculus?
-An expression is 'fully contracted' when all of its tensor indices are paired off in such a way that each index is summed over, resulting in a scalar value. This is important for obtaining invariant expressions.
How does the video conclude about the transformation of the partial derivative of a scalar function?
-The video concludes that the partial derivative of a scalar function does transform as a tensor, as its transformation equation fits the required tensor transformation pattern, with the dummy index on one side matching the free index on the other.
Outlines
📚 Introduction to Transformation Equations for Partial Derivatives
In this segment, the video introduces the concept of deriving transformation equations for partial derivatives in the context of tensor calculus. The divergence, a scalar function that measures the inflow or outflow within a space, is discussed in relation to vector fields. The goal is to express this concept as a tensor equation, which would be invariant across all coordinate systems. The video begins by representing the divergence in Cartesian coordinates and then explores the challenges of transforming this expression into a tensor calculus form, including the issue of covariant and contravariant components.
🔍 Deriving the Transformation Equation for Partial Derivatives
This paragraph delves into the process of deriving the transformation equation for partial derivatives. It starts by examining the transformation of contravariant vector components and the need to apply a contravariant transformation to obtain the value in the unprimed system. The video uses the chain rule and the Jacobian matrix to derive the transformation relationship for the partial derivative. The discussion highlights that the partial derivative of a contravariant vector component does not transform as a tensor due to the presence of an additional term in the transformation equation.
📘 Transformation Equation for Covariant Vector Components
The video script continues with the derivation of the transformation equation for covariant vector components. It explains that covariant components transform using a covariant transformation rule. The process involves taking the partial derivative of both sides of the covariant transformation with respect to zj, which requires the use of the product rule. The script introduces a new syntax convention for second-order derivatives and concludes that, similar to contravariant components, the partial derivative of a covariant vector component is not a tensor due to the extra terms in the transformation equation.
🔑 Scalar Function Transformation and the Covariant Derivative
In the final paragraph, the script discusses the transformation of the partial derivative of a scalar function, which does transform as a tensor. It contrasts this with the findings from previous paragraphs, where the partial derivatives of vector components did not transform as tensors. The video concludes by highlighting the upcoming introduction of a new operator, the covariant derivative, which will address the issues encountered in transforming partial derivatives of vector components.
Mindmap
Keywords
💡Tensor Calculus
💡Divergence
💡Cartesian Coordinates
💡Scalar Function
💡Vector Field
💡Covariant and Contravariant Components
💡Tensor Equation
💡Transformation Equation
💡Chain Rule
💡Jacobian
💡Covariant Derivative
Highlights
Introduction to deriving transformation equations for partial derivatives in tensor calculus.
Explanation of the divergence in relation to Cartesian coordinates and its physical interpretation as a measure of inflow and outflow.
The concept of divergence in fluid dynamics, where it is expected to be zero for incompressible fluids.
Importance of divergence in electricity, magnetism, and gravitation.
The goal to develop a tensor calculus expression for the divergence that is invariant across all coordinate systems.
Expression of Cartesian coordinates as indexes and the problem of covariant indexes in the divergence expression.
The realization that the components of a vector field can be represented as both covariant and contravariant components.
The attempt to create a tensor equation for the divergence and the challenges encountered with covariant and contravariant components.
Derivation of the transformation equation for a partial derivative to determine if it is a tensor.
The use of the chain rule and the Jacobian matrix in deriving the transformation equation for partial derivatives.
The discovery that the partial derivative of a contravariant vector component does not transform as a tensor due to additional terms.
Introduction of a new syntax convention for second-order derivatives in the Jacobian matrix.
Derivation of the transformation equation for the partial derivative of a covariant object and its implications.
Conclusion that the partial derivative of a scalar function transforms as a tensor, unlike vector components.
The impact of these findings on the development of expressions involving partial derivatives of vector components.
Introduction of the covariant derivative as a solution to the problem encountered in this video.
Recap of the video's findings and the implications for future discussions on tensor calculus and the divergence.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: