Video 29 - Christoffel Symbol Transformation

Tensor Calculus

5 Sept 202321:18

EducationalLearning

32 Likes 10 Comments

TLDRThis video delves into the Christoffel symbol of tensor calculus, deriving its transformation equation and exploring its properties. The script explains how the Christoffel symbol, despite not being a tensor itself, plays a crucial role in defining the covariant derivative, which is a tensor. The video clarifies the distinction between the Christoffel symbol's first and second kind, discusses its symmetry, and illustrates how the covariant derivative captures both the physical change of a vector and the change due to varying basis vectors in curved spaces, providing insight into its significance in differential geometry.

Takeaways

📚 The video script is part of a series on tensor calculus, specifically focusing on the Christoffel symbol, which is a set of scalar functions used in differential geometry.
🔍 The Christoffel symbol is derived from the dot product of the covariant basis vector and the contravariant basis vector, leading to an explicit formula for the symbol in terms of the metric tensor.
🔄 The script discusses the transformation of the Christoffel symbol and its equivalence in flat manifolds, but also highlights that it's a more general definition suitable for both flat and curved spaces.
📐 The Christoffel symbol can be represented in two forms: the first kind with all indices in the lower position and the second kind with one index in the upper position, both forms carrying the same information.
🔗 The transformation of the Christoffel symbol involves expressing it in terms of new coordinates using the Jacobian matrix and the chain rule for partial derivatives.
🚫 The Christoffel symbol is not a tensor, as its transformation rule includes an additional term that does not fit the tensor transformation pattern.
🔑 The covariant derivative, which combines the partial derivative and the Christoffel symbol, is a tensor, illustrating the principle that the sum of two non-tensor terms can result in a tensor.
🌐 The covariant derivative captures the effects of both the physical change of a vector field and the change in basis vectors due to the curvature of the space.
📈 The script provides insight into the practical application of the covariant derivative in non-Cartesian coordinate systems, such as polar coordinates, where basis vectors change with position.
📝 The video concludes with a recap of the main points, emphasizing the importance of the covariant derivative in tensor calculus and its ability to represent changes in vector components in curved spaces.
📚 The next video in the series will demonstrate how to evaluate the Christoffel symbol for specific coordinate systems, providing a practical application of the concepts discussed.

Q & A

What is the Christoffel symbol in tensor calculus?
-The Christoffel symbol is a set of scalar functions used to represent vectors as linear combinations in a manifold. It is crucial in the study of curvature and in defining the covariant derivative.
How is the Christoffel symbol derived from the equation involving the covariant basis vector?
-The Christoffel symbol is derived by dotting both sides of the equation with the contravariant basis vector and simplifying to isolate the symbol on one side of the equation.
Why is the definition of the Christoffel symbol with all lower indices considered more appropriate than the original definition?
-The definition with all lower indices is more appropriate because it works for both flat and curved surfaces or manifolds, unlike the original definition which is only equivalent in flat spaces.
What is the relationship between the Christoffel symbol of the first kind and the second kind?
-The Christoffel symbol of the first kind has all indices in the lower position, while the second kind has the I index in the upper position. They are different aspects of the same object and can be converted into each other through contraction with the covariant metric tensor.
How does the transformation of the Christoffel symbol differ from that of a tensor?
-The transformation of the Christoffel symbol includes an additional term that makes it not a tensor, unlike the transformation of tensors which follow the standard transformation rules without extra terms.
Why is the covariant derivative considered a tensor despite being composed of the partial derivative and the Christoffel symbol, which are not tensors?
-The covariant derivative is a tensor because it follows the quotient theorem, which allows the sum of two non-tensor terms to result in a tensor when combined in a specific way.
What is the significance of the symmetry between the last two indices in the Christoffel symbol?
-The symmetry between the last two indices (J and K) indicates that these indices can be interchanged without changing the value of the Christoffel symbol, reflecting the geometric properties of the space.
How does the covariant derivative capture the effects of both the physical change of a vector and the change in basis vectors?
-The covariant derivative combines the physical change of the vector with the change in basis vectors by adding the partial derivative and the term involving the Christoffel symbol, thus accounting for both effects simultaneously.
What insight does the script provide about the covariant derivative in the context of polar coordinates?
-In polar coordinates, the covariant derivative accounts for the change in vector components due to the change in basis vectors' orientation, as well as any physical change in the vector itself as it moves along a path.
Why is the covariant derivative important in the study of curved spaces?
-The covariant derivative is important in curved spaces because it provides a way to measure the change in vectors and their components in a way that is invariant under coordinate transformations, which is essential for understanding the intrinsic properties of the space.

Outlines

00:00

📚 Introduction to Christofel Symbols and Transformation Equation

This paragraph delves into the exploration of the Christofel symbol, a set of scalar functions used to represent vectors as linear combinations. The speaker begins by manipulating the equation involving the Christofel symbol, introducing a new definition that is more suitable for both flat and curved manifolds. The paragraph concludes with the isolation of the Christofel symbol and a comparison of its definition in flat spaces versus curved surfaces, emphasizing the generality of the new definition.

05:02

🔍 Deriving the Christofel Symbol's Transformation Rule

The speaker continues by renaming indices and multiplying both sides of the equation by the covariant metric tensor, leading to a new object with all lower indices. This new object is related to the Christofel symbol but in a different form, similar to how covariant and contravariant vector components relate to each other. The paragraph introduces the concept of the Christofel symbol of the first and second kind, discusses different notational conventions used by various authors, and highlights the symmetry between the last two indices of the symbol.

10:04

🔬 Examining the Christofel Symbol's Tensorial Nature

In this section, the focus shifts to determining whether the Christofel symbol is a tensor by deriving its transformation equation. The process involves expressing the right-hand side of the equation in terms of new coordinates using the contravariant and covariant transformation rules, along with the application of the product rule and the chain rule. The final transformation rule for the Christofel symbol is presented, and it is concluded that the symbol itself is not a tensor due to the presence of an additional term in its transformation equation.

15:06

🌐 Understanding the Covariant Derivative and Its Significance

The speaker provides insight into the covariant derivative, explaining how it captures both the physical change of a vector and the change in its components due to the movement along a path in a space with changing basis vectors. The covariant derivative is shown to be a tensor, formed by the sum of a partial derivative and the Christofel symbol, neither of which are tensors on their own. This illustrates the principle that non-tensor terms can combine to form a tensor, and the covariant derivative is highlighted as an expression that accounts for both the intrinsic change of a vector and the change due to the coordinate system.

20:08

📝 Recap and Preview of Future Content

The final paragraph provides a recap of the key points discussed in the video: the derivation of the Christofel symbol's explicit formula, the lowering of indices using the covariant metric tensor, the distinction between the first and second kind of Christofel symbols, and the derivation of the symbol's transformation rule. It concludes with a preview of the next video, which will demonstrate how to evaluate the Christofel symbol for specific coordinate systems.

Mindmap

Keywords

💡Christofel Symbol

The Christofel Symbol is a set of scalar functions used in differential geometry to describe the curvature of a manifold. In the video, it is introduced as a crucial element for representing vectors as linear combinations and deriving its transformation equation. It is also discussed in the context of its two forms: the first kind and the second kind, which are different aspects of the same concept.

💡Covariant Basis Vector

A covariant basis vector is a vector in a tangent space of a manifold that changes in a specific way when the coordinates are transformed. In the script, the covariant basis vector is used in the dot product to simplify expressions and derive the Christofel symbol, showing its role in tensor calculus.

💡Contravariant Basis Vector

The contravariant basis vector is dual to the covariant basis vector and is used to transform in the opposite way under coordinate transformations. In the video, it is mentioned in the context of dotting both sides of an equation with this vector to lead to the derivation of the Christofel symbol.

💡Transformation Equation

A transformation equation describes how quantities change under a coordinate transformation. The video focuses on deriving the transformation equation for the Christofel symbol, which is essential for understanding its behavior under different coordinate systems.

💡Covariant Metric Tensor

The covariant metric tensor is a key element in differential geometry that provides a way to measure distances and angles in a curved space. In the script, it is used to lower the index of the Christofel symbol, demonstrating its role in tensor operations.

💡Flat Manifold

A flat manifold is a geometric space that is locally similar to Euclidean space, meaning it has no intrinsic curvature. The video mentions that in flat manifolds, certain expressions for the Christofel symbol are equivalent, which is a simplifying condition for calculations.

💡Curved Surface

A curved surface is a type of manifold that has intrinsic curvature, unlike a flat manifold. The script discusses that the definition of the Christofel symbol derived is more appropriate because it works for both flat and curved surfaces, emphasizing its generality.

💡Symmetry

In the context of the Christofel symbol, symmetry refers to the interchangeable nature of certain indices, indicating that the symbol's value does not change when these indices are swapped. The script points out the symmetry between the last two indices of the Christofel symbol.

💡Tensor

A tensor is a mathematical object that generalizes scalars, vectors, and other quantities in a way that is applicable to curved spaces. The video explores whether the Christofel symbol is a tensor and concludes that it is not, based on its transformation properties.

💡Covariant Derivative

The covariant derivative is a derivative that generalizes the directional derivative to curved spaces. It is shown in the video to be a combination of the partial derivative and the Christofel symbol, resulting in a tensor despite the individual components not being tensors themselves.

💡Polar Coordinates

Polar coordinates are a two-dimensional coordinate system in which each point is determined by a distance from a reference point and an angle from a reference direction. The video uses polar coordinates as an example to explain the physical interpretation of the covariant derivative and the effect of basis vector changes.

Highlights

Introduction to the Christoffel symbol and its role in tensor calculus.

Derivation of the transformation equation for the Christoffel symbol.

Explanation of the dot product between covariant and contravariant basis vectors resulting in the Delta function.

Isolation of the Christoffel symbol in an equation to provide an explicit formula.

Discussion on the equivalence of two expressions for the Christoffel symbol in flat manifolds.

Introduction of a more general definition for the Christoffel symbol applicable to both flat and curved surfaces.

Renaming of indices and multiplication by the covariant metric tensor to explore the Christoffel symbol.

Introduction of the Christoffel symbol of the first and second kind, and their relationship.

Explanation of the symmetry between the last two indices in the Christoffel symbol.

Demonstration of the transformation of the Christoffel symbol using Z Prime coordinates.

Use of the product rule and chain rule in the derivation of the Christoffel symbol's transformation.

Conclusion that the Christoffel symbol is not a tensor due to its transformation rule.

Insight into the covariant derivative as a combination of a non-tensor partial derivative and the Christoffel symbol.

Discussion on the covariant derivative capturing both the physical change of a vector and the change due to basis vectors.

Illustration of how the covariant derivative works in Cartesian versus polar coordinates.

Recap of the video's main points and the significance of the derived expressions for the Christoffel symbol.

Preview of the next video's content focusing on evaluating the Christoffel symbol for specific coordinate systems.

Transcripts

Browse More Related Video

Tensor Calculus 6a: The Christoffel Symbol

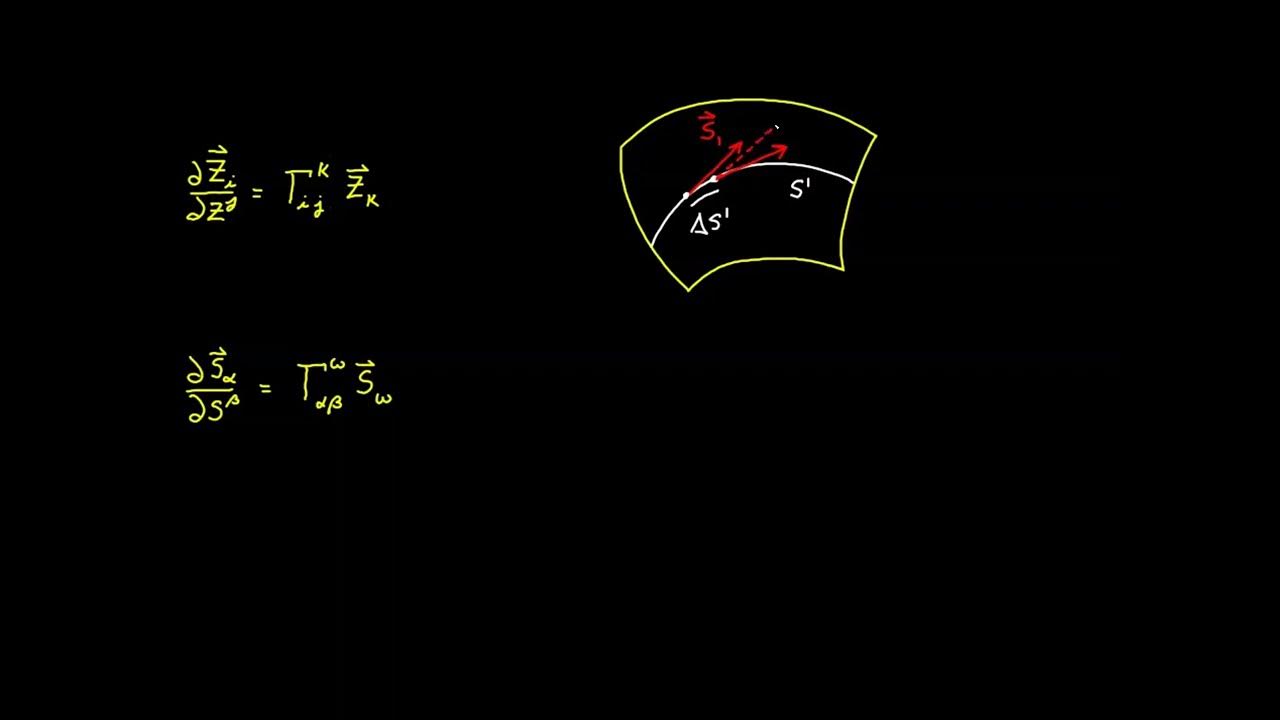
Video 68 - Christoffel Symbol for Surfaces - Part 1

Video 28 - Covariant Derivative for Contravariant Vector

Tensor Calculus Lecture 6c: The Covariant Derivative 2

Tensor Calculus 19: Covariant Derivative (Intrinsic) and Geodesics

Tensor Calculus 17.5: Covariant Derivative (Component Definition) - Optional

Related Tags

Tensor Calculus Christoffel Symbol Flat Manifolds Curved Surfaces Covariant Derivative Vector Fields Partial Derivatives Metric Tensor Jacobian Transformation Polar Coordinates Cartesian Coordinates