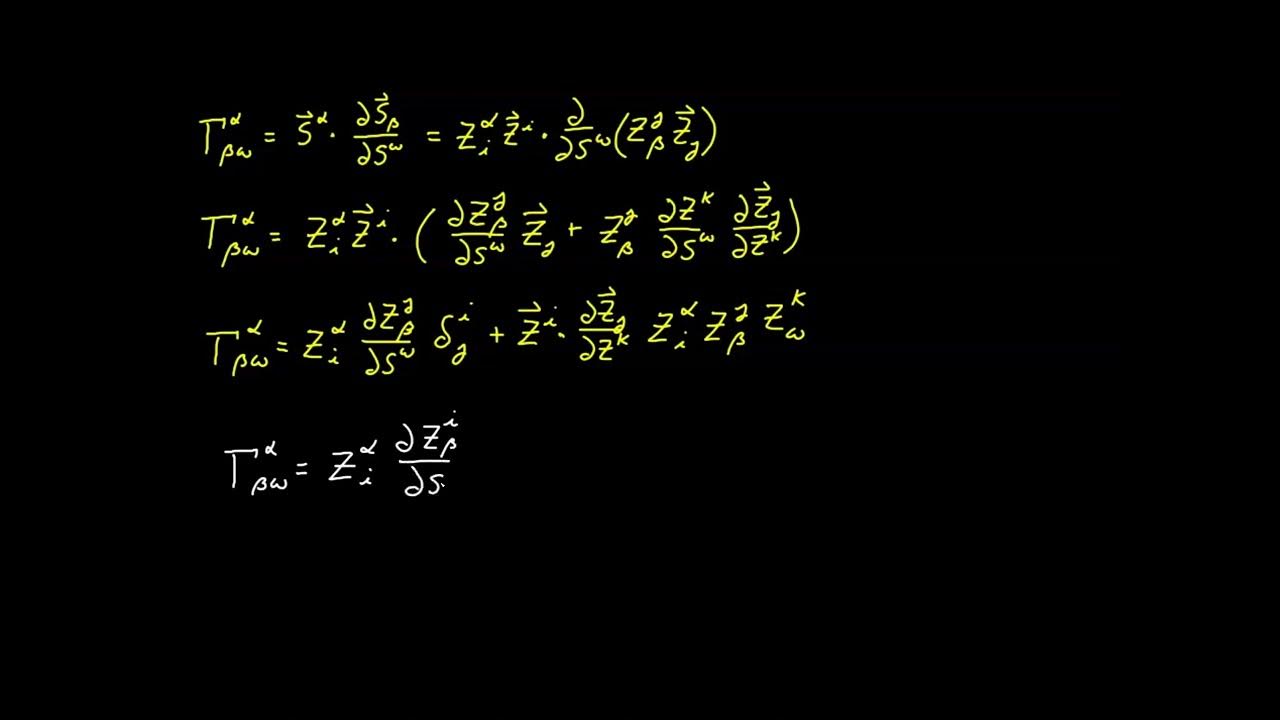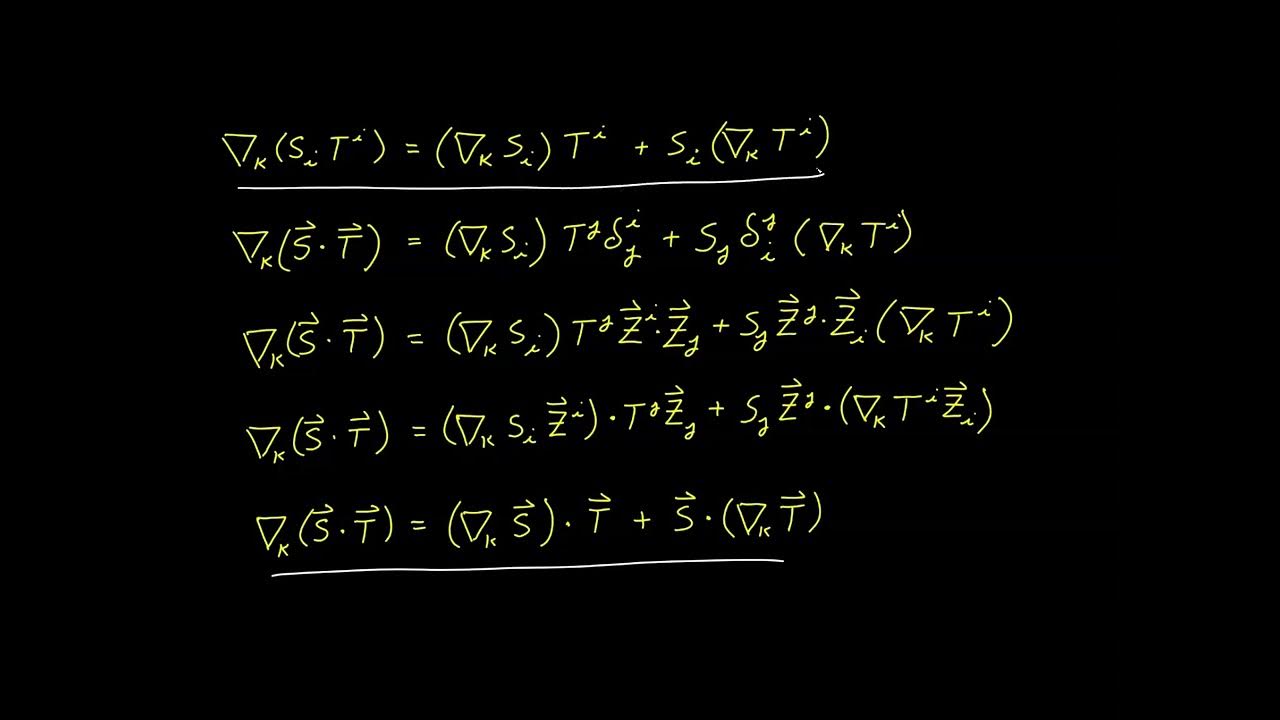Video 30 - Christoffel Symbol Evaluation

Tensor Calculus
5 Sept 202315:02
EducationalLearning
32 Likes 10 Comments

TLDRIn this video, the presenter dives into tensor calculus, focusing on the derivation of a formula to evaluate the Christoffel symbols for any coordinate system. They start by explaining the basic definition and computation using covariant basis vectors and partial derivatives but soon introduce a more efficient method involving the covariant metric tensor. The presenter demonstrates how to permute indices and derive explicit formulas for both the first and second kind of Christoffel symbols, simplifying the process to just requiring metric tensors, eliminating the need for basis vectors and dot products. The video concludes with a recap and a preview of applying these formulas to various coordinate systems in the next video.

Takeaways
  • 📚 The video continues an in-depth analysis of the Christoffel symbol, focusing on deriving a formula to evaluate it for any coordinate system.
  • 🔍 One method to evaluate Christoffel symbols is through their basic definitions, involving covariant basis vectors and dot products with their partial derivatives.
  • 📐 The example given uses plane polar coordinates to calculate the Christoffel symbol of the first kind, showing the process of finding the dot product between basis vectors and their derivatives.
  • 🔢 The calculation results in the Christoffel symbol being a function of the coordinate values, specifically R and Theta in plane polar coordinates, and simplifies to R for the given example.
  • 🤔 The direct method of calculating Christoffel symbols can be tedious due to the multiple indices and the need to perform the process 16 times for all possible symbols.
  • 🆕 An alternative, more convenient formula is introduced that simplifies the calculation of Christoffel symbols using the partial derivatives of the covariant metric tensor.
  • 🔄 The derivation of this formula involves permuting indices and using the commutative property of dot products to simplify and isolate the Christoffel symbols.
  • 📉 The final formula for the Christoffel symbol of the first kind does not require basis vectors or dot products, streamlining the calculation process.
  • 🆙 To find the Christoffel symbol of the second kind, the formula for the first kind is used, and the index is raised by contracting with the contravariant metric tensor.
  • 📝 The video concludes with a recap of the derived formulas for both types of Christoffel symbols, emphasizing their utility in tensor calculus and the simplification they provide over the direct method.
  • 📚 The next step is to apply these formulas to various coordinate systems to evaluate the Christoffel symbols, demonstrating the practicality of the derived relationships.
Q & A

  • What is the primary focus of video 30 in the Tensor Calculus series?

    -The primary focus of video 30 is to continue the analysis of the Christoffel symbols, particularly by deriving a formula that allows the evaluation of Christoffel symbols for any coordinate system.

  • How can the Christoffel symbols be evaluated using their basic definitions?

    -Christoffel symbols can be evaluated by using their basic definitions, which involve finding the covariant basis vector and taking its partial derivative with respect to another coordinate. The result is then dotted with the basis vector to obtain the Christoffel symbol.

  • Why might the basic method for calculating Christoffel symbols be considered tedious?

    -The basic method is tedious because it requires calculating the covariant basis vector, taking its partial derivative, and finding the dot product for each possible combination of indices. Since there are multiple combinations, this process must be repeated many times, making it cumbersome.

  • What is the advantage of the alternative formula for Christoffel symbols mentioned in the video?

    -The alternative formula for Christoffel symbols is more convenient because it only requires the partial derivatives of the covariant metric tensor, eliminating the need for basis vectors or dot products. This simplifies the calculation process significantly.

  • How is the partial derivative of the covariant metric tensor related to the Christoffel symbols?

    -The partial derivative of the covariant metric tensor with respect to a coordinate is equal to the sum of two Christoffel symbols. This relationship is derived by applying the product rule to the definition of the covariant metric tensor.

  • What is meant by 'permuting the indices' in the context of this video?

    -'Permuting the indices' refers to cyclically renaming the indices in the equation for the Christoffel symbols. This process is used to derive additional equations, which can be combined to simplify the expression for the Christoffel symbols.

  • How does the formula for the Christoffel symbols of the first kind differ from the basic method?

    -The formula for the Christoffel symbols of the first kind, derived in the video, is based solely on the partial derivatives of the covariant metric tensor. It avoids the need for calculating covariant basis vectors and dot products, making it more straightforward and less tedious.

  • How is the Christoffel symbol of the second kind related to the first kind?

    -The Christoffel symbol of the second kind is obtained by raising one of the indices of the Christoffel symbol of the first kind using the contravariant metric tensor. This process contracts the contravariant metric tensor with the Christoffel symbol of the first kind.

  • Why is the derived formula for the Christoffel symbols considered advantageous?

    -The derived formula is advantageous because it only requires the covariant and contravariant metric tensors for the calculations. This simplifies the process, making it easier to evaluate Christoffel symbols for any coordinate system without needing to compute basis vectors or dot products.

  • What will be covered in the next video following this one?

    -In the next video, the focus will be on applying the derived formulas to evaluate all the Christoffel symbols of the first and second kinds for various sample coordinate systems.

Outlines
00:00
📚 Introduction to Christoffel Symbols Evaluation

This paragraph introduces the topic of the video, which is the derivation of a formula to evaluate Christoffel symbols for any coordinate system. It explains the basic method of finding Christoffel symbols by using their definitions and gives an example using plane polar coordinates. The paragraph also highlights the tediousness of this method due to the multiple calculations required for different index values and introduces the idea of a more convenient formula.

05:02
🔍 Derivation of a Convenient Formula for Christoffel Symbols

The second paragraph delves into a derivation that simplifies the evaluation of Christoffel symbols. It starts by discussing the partial derivative of the covariant metric tensor and uses the definition of the Christoffel symbol of the first kind. The process involves permuting the indices of the tensor and using the product rule, leading to a cancellation of terms and the derivation of an explicit formula for the Christoffel symbol of the first kind based on the partial derivatives of the metric tensor. The paragraph also mentions the potential to simplify the calculation of the second kind of Christoffel symbols.

10:02
📘 Application of the Derived Formula and Recap

In this final paragraph, the application of the derived formula is demonstrated by recalculating a Christoffel symbol for plane polar coordinates, showing the ease of use compared to the initial method. The paragraph also explains how to derive the Christoffel symbol of the second kind by raising the index and contracting with the contravariant metric tensor. The summary concludes with a recap of the video's achievements, emphasizing the utility of the new formulas for evaluating Christoffel symbols based solely on the metric tensor, thus simplifying the process significantly.

Mindmap
Keywords
💡Christoffel Symbol
The Christoffel symbol is a function that arises in differential geometry and general relativity, representing the curvature of a manifold. In the context of the video, it is used to evaluate the curvature within different coordinate systems, such as plane polar coordinates. The script discusses how to derive formulas for the Christoffel symbols of the first and second kind, which are essential for tensor calculus.
💡Covariant Basis Vector
A covariant basis vector is a vector that is tangent to a coordinate curve and changes with the coordinate system. In the script, the covariant basis vector C2 is mentioned as a necessary component for calculating the Christoffel symbol of the first kind, where it is used to find the dot product with its partial derivative.
💡Partial Derivative
A partial derivative is a derivative of a function with respect to one variable, while the other variables are held constant. In the video, the partial derivative is used in the calculation of the Christoffel symbols, specifically in finding the derivative of the covariant basis vector with respect to a certain coordinate.
💡Dot Product
The dot product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number. In the script, the dot product is used to combine the covariant basis vector with its partial derivative in the calculation of the Christoffel symbol.
💡Polar Coordinates
Polar coordinates are a two-dimensional coordinate system in which each point is determined by a distance from a reference point and an angle from a reference direction. The script uses plane polar coordinates as an example to demonstrate the calculation of the Christoffel symbols.
💡Covariant Metric Tensor
The covariant metric tensor is a key concept in differential geometry, which provides a way to measure distances and angles in a curved space. In the video, the covariant metric tensor is used to derive the partial derivatives needed for the Christoffel symbols.
💡Product Rule
The product rule is a fundamental calculus rule used to find the derivative of a product of two functions. The script mentions the product rule in the context of finding the partial derivative of the covariant metric tensor.
💡Index Permutation
Index permutation is a technique used in tensor calculus where the indices of a tensor are rearranged in a specific order to derive new relationships or simplify expressions. The script describes how index permutation is used to derive an explicit formula for the Christoffel symbol of the first kind.
💡Contravariant Metric Tensor
The contravariant metric tensor is a tensor that is used to 'raise' the indices of other tensors, effectively converting between covariant and contravariant vectors. In the script, the contravariant metric tensor is used to derive the Christoffel symbol of the second kind from the first kind.
💡Tensor Calculus
Tensor calculus is a field of mathematics that extends the methods of vector calculus to tensor fields. The video is part of a series on tensor calculus, focusing on the derivation and application of the Christoffel symbols within various coordinate systems.
💡Metric Tensor
The metric tensor is a fundamental concept in differential geometry, defining the geometry of a space by specifying how to measure distances and angles. The script emphasizes the importance of the metric tensor in calculating the Christoffel symbols without the need for basis vectors or dot products.
Highlights

Derivation of a formula to evaluate Christoffel symbols for any coordinate system.

Explanation of evaluating Christoffel symbols using basic definitions and covariant basis vectors.

Demonstration of calculating the Christoffel symbol of the first kind 221 in plane polar coordinates.

Introduction of a more convenient formula for Christoffel symbols based on the covariant metric tensor.

Derivation of the relationship between the covariant metric tensor and Christoffel symbols using the product rule.

Description of the process of index permutation in tensor calculus.

Showcasing the cancellation of terms after index permutation to derive an explicit formula for Christoffel symbols.

Simplification of the calculation of Christoffel symbols using the derived formula without the need for basis vectors or dot products.

Application of the new formula to re-evaluate the Christoffel symbol 221 in plane polar coordinates.

Introduction of a method to derive the Christoffel symbol of the second kind by raising the index.

Explanation of contracting the contravariant metric tensor with the Christoffel symbol of the first kind to obtain the second kind.

Emphasis on the practicality of using the metric tensor for straightforward calculation of Christoffel symbols.

Recap of the video's content, highlighting the importance of the derived formulas for Christoffel symbols.

Discussion on the utility of the derived formulas in future videos and their applications.

Recommendation to work through all Christoffel symbols of the first kind before raising indices for the second kind.

Preview of the next video's content, which will involve evaluating Christoffel symbols for sample coordinate systems.

Transcripts

Browse More Related Video

Video 70 - Surface Christoffel Examples

Video 31 - Christoffel Symbol Examples

Video 69 - Christoffel Symbol for Surfaces - Part 2

Video 17 - Contravariant Basis

Video 37 - Metrinilic Property - Part 1

Video 24 - Dot Product

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Tensor CalculusChristoffel SymbolsCoordinate SystemsPolar CoordinatesMetric TensorPartial DerivativesDot ProductMathematics EducationAdvanced MathCalculus TutorialVector Analysis