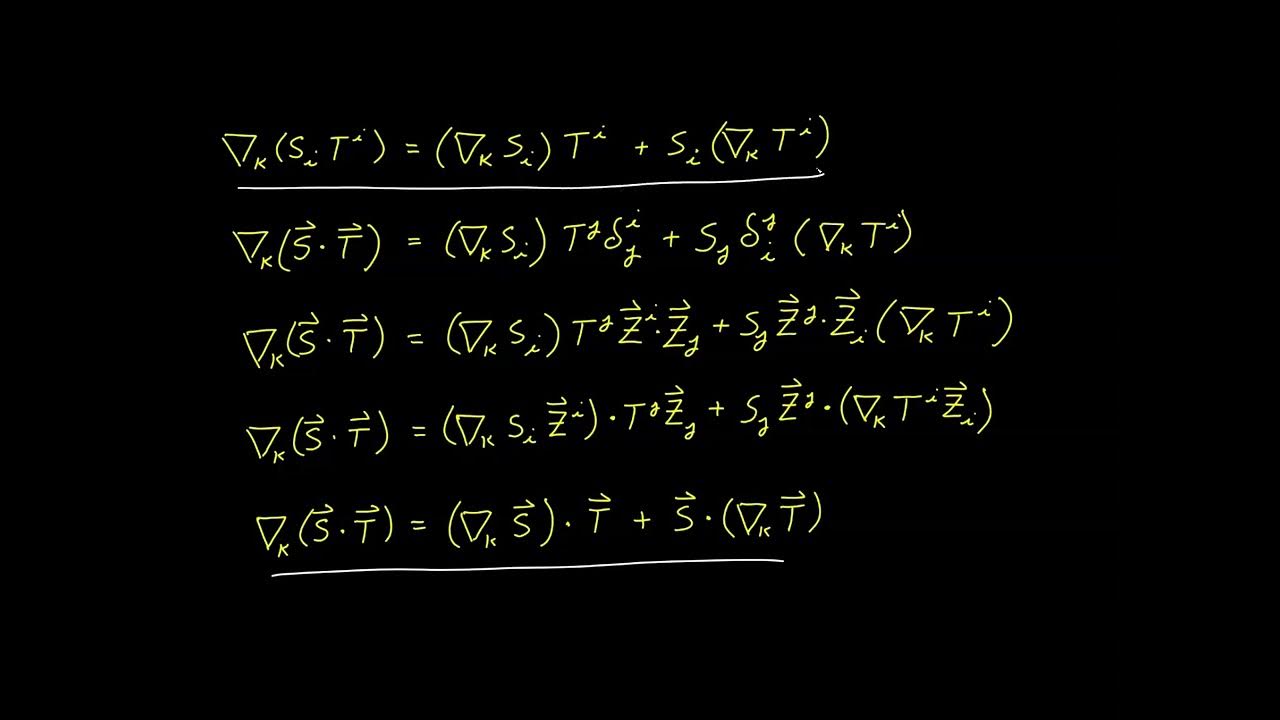Video 26 - Vector Operation Examples

Tensor Calculus

4 Jun 202220:22

EducationalLearning

32 Likes 10 Comments

TLDRThis video from a tensor calculus series demonstrates practical applications of concepts introduced in previous episodes. The instructor sets specific values for parameters, simplifies metric tensors, and defines vectors using covariant and contravariant bases. The video illustrates vector transformations to Cartesian coordinates using contravariant components and the Jacobian matrix. It also explores calculating the dot product in various ways, emphasizing its invariance across coordinate systems, reinforcing the geometric nature of the operation. The lesson encourages hands-on practice to solidify understanding of tensor calculus techniques.

Takeaways

📚 This video is part of a series on tensor calculus, focusing on illustrating operations with specific vectors using concepts from previous videos.
🔍 The video introduces covariant and contravariant metric tensors for affine coordinates, setting specific values for parameters like scaling factors and skew angles.
📐 The instructor demonstrates the conversion of metric tensors into a simplified form by setting the cosine and sine of the skew angle to specific values.
📝 The script encourages viewers to pause and validate the results of metric tensor simplification themselves, promoting active learning.
📈 Vectors 'u' and 'v' are defined in terms of the covariant basis, with the components being contravariant, indicated by the lower index.
🔄 The video shows how to convert the vectors to a linear combination form using the contravariant basis, which involves lowering the index using a specific formula.
📉 The transformation of vectors from affine coordinates to Cartesian coordinates is explained, utilizing the contravariant components and the Jacobian matrix.
📊 The script includes a detailed calculation of the dot product of vectors 'u' and 'v' using different tensor calculus formulas, emphasizing the invariance of the dot product.
🔢 The video confirms the invariance of the dot product by showing that it yields the same result regardless of the coordinate system used, reinforcing the concept of geometric invariance.
📚 The final takeaway emphasizes the importance of practicing with tensor calculus techniques to deepen understanding and benefit from the concepts in the long run.
🔚 The video concludes with an invitation to the next session, encouraging ongoing engagement with the series.

Q & A

What is the main topic of this video?
-The main topic of this video is to illustrate several tensor calculus operations using specific vectors and metric tensors in the context of affine coordinates.
What are the covariant and contravariant metric tensors?
-The covariant and contravariant metric tensors are mathematical objects that describe the geometry of a space in terms of distances and angles, and they are used in tensor calculus to perform various operations.
What specific values are set for the parameters in the video?
-The scaling factors are set to 1, and the skew angle is set to pi over three, which results in the cosine of alpha being one half and the sine of alpha being the square root of three over two.
How are the vectors u and v defined in the video?
-The vectors u and v are defined in terms of the covariant basis, with their components being contravariant components due to the lower index notation.
What is the process of converting a vector from covariant to contravariant components?
-The process involves lowering the index of the covariant components using the formula u_i = z^i_j * u^j, where z^i_j are the components of the metric tensor.
What is the significance of expressing vectors in both covariant and contravariant forms?
-Expressing vectors in both forms allows for flexibility in performing various tensor operations and transformations, which is essential in tensor calculus.
What is the purpose of the Jacobian matrix in the context of this video?
-The Jacobian matrix is used for the transformation between affine coordinates and Cartesian coordinates, allowing the conversion of vector components from one coordinate system to another.
How is the dot product of two vectors calculated in tensor calculus?
-The dot product in tensor calculus is calculated using the invariant formula, which involves the metric tensor and the components of the two vectors, and it results in the same value regardless of the coordinate system used.
What does the dot product being an invariant signify?
-The dot product being an invariant signifies that it is a geometric object that retains the same value across different coordinate systems, emphasizing its importance in tensor calculus.
What is the final message of the video regarding the learning process?
-The final message is that practical experience with tensor calculus techniques, such as working through examples, is crucial for understanding and benefiting from the concepts.

Outlines

00:00

📚 Introduction to Tensor Calculus with Specific Vectors

This paragraph introduces the 26th video in a series on tensor calculus, focusing on using specific vectors to demonstrate various operations covered in previous lessons. The instructor sets specific values for parameters, such as scaling factors and skew angles, leading to the resolution of covariant and contravariant metric tensors for affine coordinates. The basis vectors are defined with lower indices, indicating contravariant components. Two vectors, u and v, are introduced using the covariant basis, and the process of converting them to a contravariant basis is explained using the lowering index formula.

05:01

🔍 Vector Transformation and Cartesian Coordinates

The second paragraph continues the discussion on vectors by exploring their representation in Cartesian coordinates. A contravariant transformation is performed using the contravariant components of the vectors and the Jacobian matrix, which is derived from the specific parameter values set earlier. The process involves applying the Jacobian to convert the contravariant components of vectors u and v into Cartesian coordinates, resulting in expressions for u and v in terms of x and y components.

10:03

📘 Contravariant Transformation and Dot Product Calculation

In this paragraph, the focus shifts to the contravariant transformation and the calculation of the dot product using tensor calculus. The video script outlines the invariant formula for the dot product and applies it to the vectors u and v using both covariant and contravariant components. The calculations are performed step by step, demonstrating that the dot product is invariant under coordinate transformations, yielding the same result regardless of the coordinate system used.

15:04

📉 Cartesian Coordinates and Dot Product Validation

The fourth paragraph reinforces the concept of the dot product as an invariant by recalculating it using the Cartesian coordinates obtained in the previous step. The process involves multiplying the corresponding x and y components of the vectors and adding the products, confirming that the dot product remains invariant and equals -44, regardless of the coordinate system used to evaluate it.

20:05

🚀 Conclusion and Encouragement for Practical Application

The final paragraph concludes the video by emphasizing the importance of practical experience in understanding tensor calculus. The instructor encourages viewers to practice the techniques and principles discussed in the video to gain a deeper understanding and long-term benefit. The video wraps up with an invitation to join the next session, highlighting the value of hands-on experience in mastering abstract mathematical concepts.

Mindmap

Keywords

💡Tensor Calculus

Tensor calculus is a field of mathematics that deals with the manipulation of tensors, which are generalizations of scalars, vectors, and matrices to higher dimensions. In the context of the video, tensor calculus is used to illustrate operations with specific vectors in the context of affine coordinates, showing how these mathematical objects can be used to describe and analyze physical phenomena in various coordinate systems.

💡Covariant Basis

A covariant basis is a set of vectors that are used to express other vectors in a coordinate system. In the video, the covariant basis is defined in terms of the metric tensor for affine coordinates, and the script demonstrates how to convert vectors from the covariant basis to the contravariant basis, which is essential for understanding the transformation of vectors between different coordinate systems.

💡Contravariant Basis

The contravariant basis is complementary to the covariant basis and is used to express vectors in a way that is invariant under coordinate transformations. The video script shows the process of converting vectors from the covariant components to the contravariant components, which involves using the metric tensor to lower the index of the vector components.

💡Metric Tensor

The metric tensor is a key concept in differential geometry and tensor calculus, describing the geometry of a space by relating the lengths of vectors in different directions. In the video, the metric tensor is used to define the scaling factors and skew angles for affine coordinates, which are then used to calculate the components of vectors in both covariant and contravariant forms.

💡Affine Coordinates

Affine coordinates are a type of coordinate system that is particularly useful in tensor calculus for describing transformations that preserve parallelism and ratios of distances. The video script sets specific values for parameters in the affine coordinate system to demonstrate the calculation of metric tensors and the transformation of vectors.

💡Skew Angle

The skew angle, often denoted by 'alpha', is an angle that defines the orientation of a coordinate system relative to another. In the script, the skew angle is set to pi over three, which affects the cosine and sine values used in the metric tensor, and thus influences the transformation of vectors between coordinate systems.

💡Index Lowering

Index lowering is the process of converting a tensor's contravariant component (with an upper index) to its covariant component (with a lower index) using the metric tensor. The video demonstrates this process by showing how to calculate the contravariant components of vectors u and v using the metric tensor.

💡Jacobi Matrix

The Jacobi matrix is a matrix of all first-order partial derivatives of a vector-valued function. In the context of the video, the Jacobi matrix is used to transform vectors from affine coordinates to Cartesian coordinates, illustrating the contravariant transformation process.

💡Dot Product

The dot product, also known as the scalar product, is an algebraic operation that takes two equal-length sequences of numbers (usually coordinate vectors) and returns a single number. The video script explores the dot product in the context of tensor calculus, showing that it is an invariant operation that yields the same result regardless of the coordinate system used.

💡Invariant

In the context of tensor calculus, an invariant is a quantity that remains unchanged under coordinate transformations. The video emphasizes that the dot product is an invariant, meaning its value does not depend on the specific coordinate system used to calculate it, which is a fundamental property in geometry and physics.

💡Cartesian Coordinates

Cartesian coordinates are a two-dimensional coordinate system where each point is determined by its distances from two perpendicular axes, usually denoted as x and y. The video script concludes by expressing vectors u and v in Cartesian coordinates after performing a contravariant transformation, demonstrating the application of tensor calculus in a familiar coordinate system.

Highlights

Introduction of specific vectors to illustrate tensor operations in differential geometry.

Setting specific values for parameters such as scaling factors and skew angles in metric tensors.

Conversion of metric tensors to a simplified form using specific parameter values.

Definition of vectors u and v in terms of covariant basis with contravariant components.

Demonstration of converting vectors from covariant to contravariant basis using index lowering.

Calculation of contravariant components for vectors u and v using the metric tensor.

Transformation of vectors to Cartesian coordinates using contravariant transformation.

Explanation of the need for the Jacobian matrix in the transformation process.

Application of the Jacobian matrix to find Cartesian components of vector u.

Same process applied to vector v to obtain its Cartesian components.

Discussion on the possibility of using covariant transformation with the inverse Jacobian.

Calculation of the dot product using different tensor expressions and confirming their equivalence.

Verification of the dot product's invariance across different coordinate systems.

Practical application of tensor calculus techniques through worked examples.

Emphasis on the importance of practice in understanding tensor calculus concepts.

Conclusion summarizing the purpose of the video and encouraging further self-study.

Transcripts

Browse More Related Video

Video 17 - Contravariant Basis

Video 24 - Dot Product

Video 37 - Metrinilic Property - Part 1

Video 12 - Jacobian Examples

Video 40 - Gradient Examples

Video 11 - Vector Transformations

Related Tags

Tensor Calculus Vector Operations Affine Coordinates Metric Tensors Covariant Basis Contravariance Cartesian Coordinates Dot Product Jacobian Matrix Educational Content Mathematics Tutorial