Standard Deviation Formula, Statistics, Variance, Sample and Population Mean

The Organic Chemistry Tutor
12 Feb 201710:21
EducationalLearning
32 Likes 10 Comments

TLDRThis video script offers a clear and concise explanation of how to calculate the standard deviation for both a population and a sample set of numbers. It introduces the formulas for population standard deviation (sigma) and sample standard deviation (s), emphasizing the difference in the denominator (n for population, n-1 for sample). The script also explains the concept of standard deviation in terms of the spread of numbers and provides a step-by-step example for each type of standard deviation, illustrating the process with two sets of numbers. Additionally, it explains how to calculate variance, which is the square of the standard deviation. The video aims to educate viewers on these statistical concepts in an accessible manner.

Takeaways
  • 📊 Standard deviation is a measure of how spread out a set of numbers is from their mean.
  • 🔢 There are two formulas for calculating standard deviation: population standard deviation (σ) and sample standard deviation (s).
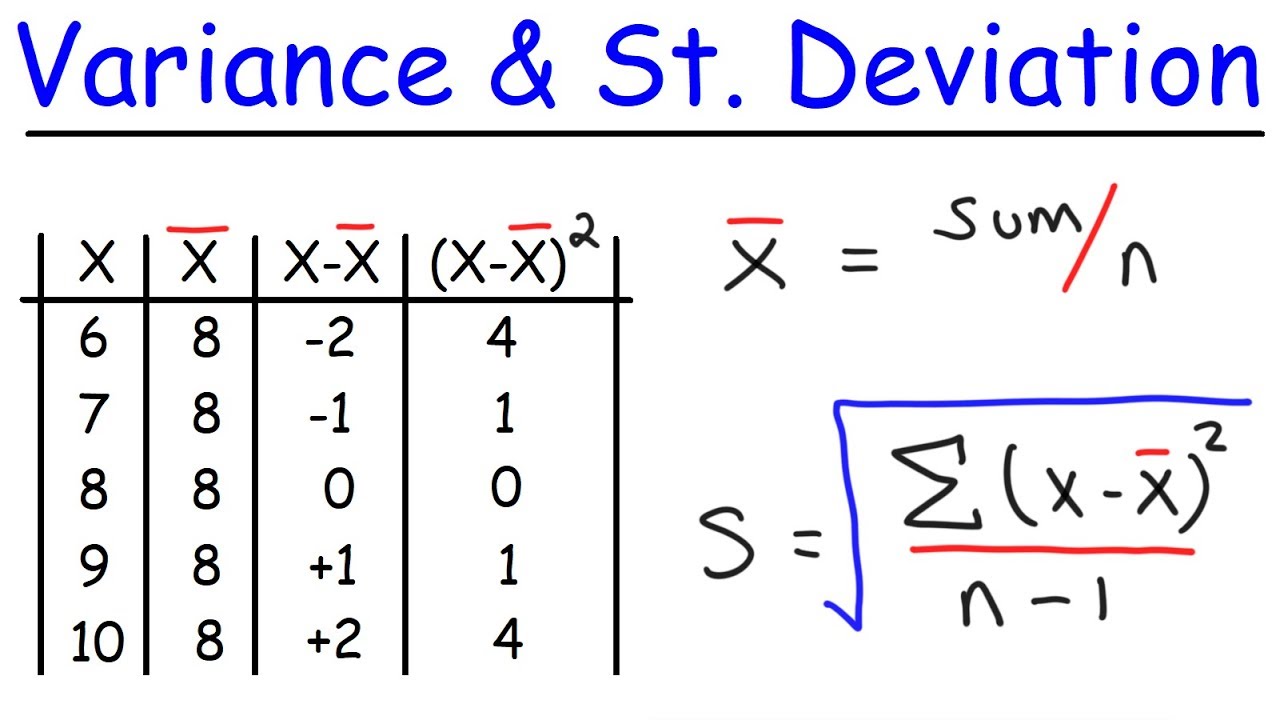
  • 🧮 Population standard deviation formula is the sum of the squared differences from the mean (μ) divided by the number of data points (n), then taking the square root.
  • 🧮 Sample standard deviation formula is similar to the population standard deviation but divides by n-1 instead of n.
  • 🤔 To guess which set of numbers has a greater standard deviation, consider how spread out the numbers are; more spread out numbers have a greater standard deviation.
  • 📐 Example set 1 (3, 5, 7) has a higher standard deviation than example set 2 (4, 5, 6) because the numbers are more spread out from their mean.
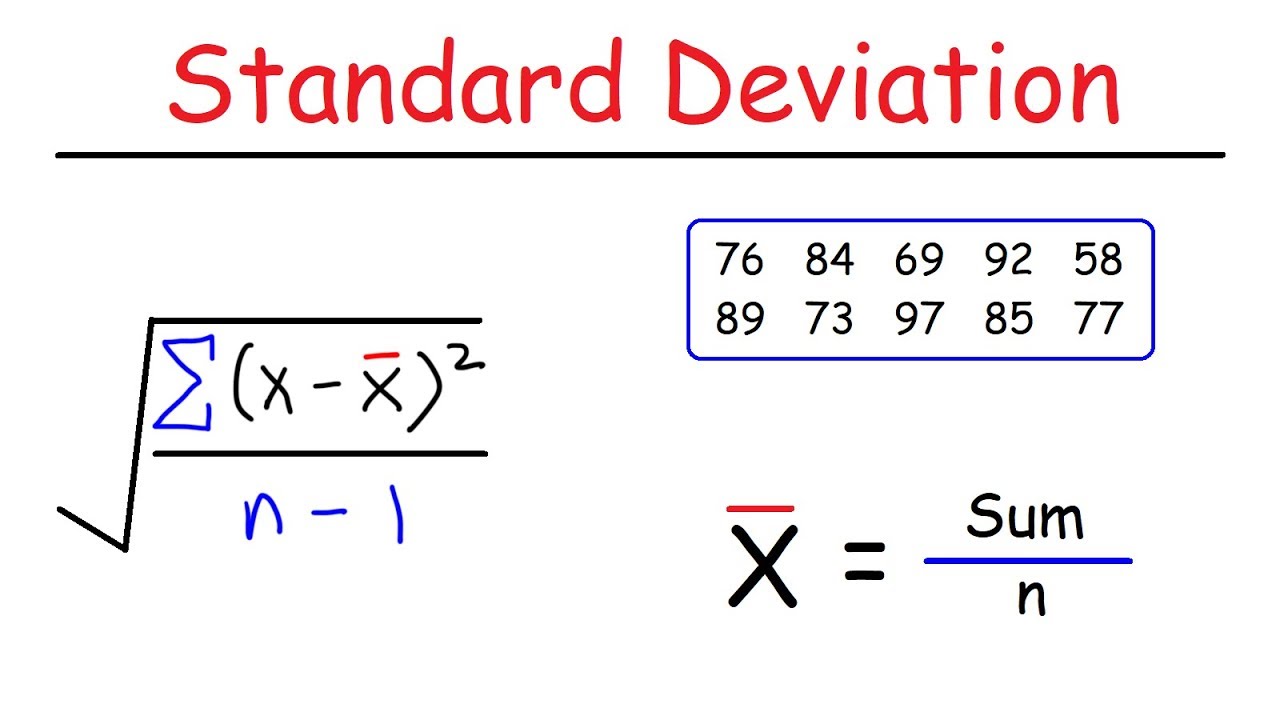
  • 📝 To calculate standard deviation, first find the mean of the data set by summing all numbers and dividing by the count.
  • 🔢 The variance is the square of the standard deviation and can be calculated using the same formula as standard deviation but without the square root.
  • 📚 Understanding standard deviation and variance is essential for various fields including algebra, calculus, chemistry, and physics.
  • 🌐 For more educational content on these subjects, one can visit the provided website or channel.
Q & A

  • What are the two formulas for calculating standard deviation mentioned in the video?

    -The two formulas mentioned for calculating standard deviation are the population standard deviation and the sample standard deviation.

  • What is the population standard deviation formula and how is it represented?

    -The population standard deviation formula is represented by the letter sigma (σ) and is calculated as the square root of the sum of the squared differences between each data point and the population mean (μ), divided by the total number of data points (n).

  • How is the sample standard deviation different from the population standard deviation?

    -The sample standard deviation is calculated using the same formula as the population standard deviation, but with a key difference. Instead of dividing by the total number of data points (n), you divide by n minus 1. This adjustment is made because we're estimating the population standard deviation from a sample.

  • What does standard deviation measure in a set of numbers?

    -Standard deviation measures how spread out the numbers are in a data set. A larger standard deviation indicates that the numbers are more dispersed from the mean, while a smaller standard deviation indicates that they are closer to the mean.

  • How do you calculate the mean for the given sets of numbers in the video?

    -The mean is calculated by summing all the numbers in the set and dividing by the number of data points. For the set 3, 5, and 7, the mean is (3 + 5 + 7) / 3 = 5. For the set 4, 5, and 6, the mean is (4 + 5 + 6) / 3 = 5.

  • What is the significance of the differences between data points and the mean in the standard deviation calculation?

    -The differences between each data point and the mean are squared to ensure that all the differences are positive, regardless of whether the data point is above or below the mean. This allows for a consistent measure of dispersion in the data set.

  • How do you calculate the variance from the standard deviation?

    -The variance is calculated by squaring the standard deviation. It represents the average of the squared differences from the mean, and provides a measure of dispersion in the same units as the data.

  • What is the result of the standard deviation calculation for the set 3, 5, and 7?

    -The standard deviation for the set 3, 5, and 7 is approximately 1.63.

  • What is the result of the standard deviation calculation for the set 4, 5, and 6?

    -The standard deviation for the set 4, 5, and 6 is approximately 0.816.

  • How does the video illustrate the concept of standard deviation visually?

    -The video uses a number line to visually represent the dispersion of the data points. The set 3, 5, and 7 is shown with the points further apart, indicating a higher standard deviation, while the set 4, 5, and 6 has points closer together, indicating a lower standard deviation.

  • What is the main difference in the calculation process between population and sample standard deviation?

    -The main difference is the denominator in the calculation. For population standard deviation, you divide by the total number of data points (n), while for sample standard deviation, you divide by n minus 1 to account for the bias in estimating the population mean from a sample.

Outlines
00:00
📊 Introduction to Standard Deviation Calculation

This paragraph introduces the concept of standard deviation, emphasizing its importance in understanding the dispersion of a data set. It outlines two formulas: the population standard deviation (represented by sigma) and the sample standard deviation. The population standard deviation is calculated by summing the squared differences between each data point and the population mean (mu), divided by the number of data points (n), and then taking the square root of the result. The sample standard deviation follows a similar formula but is divided by n minus 1 instead of n. An example is provided to illustrate which set of numbers has a greater standard deviation, highlighting that standard deviation measures how spread out the numbers are.

05:00
🧮 Calculation Steps for Sample Standard Deviation

This paragraph delves into the detailed calculation process for the sample standard deviation using the set of numbers 3, 5, and 7. It begins by calculating the mean, which is the sum of the numbers divided by the count of numbers. The mean is found to be 5. The next step involves applying the standard deviation formula, which includes squaring the differences between each number and the mean, summing these squared differences, and then dividing by the number of values (n). The result is then taken to the power of the square root to find the standard deviation. The calculation is demonstrated step by step, leading to a standard deviation of approximately 1.63 for the given set.

10:02
📈 Comparing Standard Deviations and Calculating Variance

This paragraph compares the standard deviations of two different sets of numbers: 3, 5, and 7 versus 4, 5, and 6. It explains that the set with numbers closer to each other (4, 5, and 6) will have a lower standard deviation, while the set with numbers more spread out (3, 5, and 7) will have a higher standard deviation. The calculation for the standard deviation of the second set is also demonstrated, resulting in a lower value of approximately 0.816. The paragraph concludes by explaining how to calculate variance, which is the square of the standard deviation, and provides the calculation for the given example set.

🌐 Additional Resources for Learning Mathematics and Sciences

In this final paragraph, the speaker invites viewers to explore more educational content on their channel and website, video.tutor.net. The website offers playlists on various subjects including algebra, pre-calculus, calculus, chemistry, and physics. The speaker encourages those interested to visit the website and check out the available resources for further learning and understanding of the topics covered in the video.

Mindmap
Keywords
💡Standard Deviation
Standard Deviation is a statistical measure that quantifies the amount of variation or dispersion in a set of values. It indicates how much individual data points in a dataset typically deviate from the mean (average) of the dataset. In the video, the concept is central to understanding the spread of the numbers in the given examples. The script explains two formulas for calculating standard deviation: one for a population and one for a sample. The population standard deviation is denoted by sigma and is calculated as the square root of the sum of the squared differences between each data point and the population mean, divided by the number of data points (n).
💡Population
In statistics, a population refers to the entire set of items or individuals about which data is being collected or analyzed. The population standard deviation formula mentioned in the video is used when data from the entire population is available. The video emphasizes the importance of understanding whether you are dealing with a population or a sample to choose the correct formula for calculating standard deviation.
💡Sample
A sample is a subset of a population that is used to represent and analyze the entire population. In the context of the video, the sample standard deviation is calculated when only a portion of the data from a population is available. The formula for sample standard deviation is similar to that of the population standard deviation but uses (n-1) in the denominator instead of n, which is known as Bessel's correction.
💡Mean
The mean, often referred to as the average, is a measure of central tendency that is calculated by adding up all the values in a dataset and then dividing by the number of values. In the video, the mean is a crucial intermediate step in calculating both population and sample standard deviations, as it represents the central point around which the data points are distributed.
💡Variance
Variance is a statistical measure that represents the spread of a set of numbers. It is the average of the squared differences from the mean. Essentially, variance is the square of the standard deviation, and it provides a way to quantify how much the values in a dataset deviate from the mean. In the video, the variance is calculated for the set of numbers 3, 5, and 7 by squaring the standard deviation of approximately 1.63, resulting in a variance of about 2.66.
💡Sigma (Σ)
Sigma, often used as the Greek letter Σ, is a symbol commonly used in mathematics and statistics to represent the sum of a series of terms. In the context of the video, sigma is used to denote the sum of the squared differences between each data point and the mean, which is a key component in the calculation of both population and sample standard deviations.
💡Bessel's Correction
Bessel's Correction is a statistical adjustment made when calculating the standard deviation of a sample rather than a population. It involves dividing the sum of squared differences by (n-1) instead of n, where n is the number of data points in the sample. This correction is used to provide an unbiased estimate of the population standard deviation. The video mentions this concept when explaining the difference between the sample and population standard deviation formulas.
💡Data Points
Data points refer to individual values or observations within a dataset. In the context of the video, each number in the sets of numbers provided (e.g., 3, 5, 7 and 4, 5, 6) is considered a data point. The video discusses how these data points relate to the mean and how their differences contribute to the calculation of standard deviation.
💡Spread
Spread refers to the degree of dispersion or distribution of values within a dataset. A larger spread indicates that the data points are more widely distributed from the mean, while a smaller spread indicates that the data points are more closely clustered around the mean. The standard deviation is a measure of spread, and the video uses this concept to explain how to determine which set of numbers has a greater standard deviation.
💡Calculation
Calculation refers to the process of performing mathematical operations to find a result or solution. In the video, the term is central to the explanation of how to calculate standard deviation and variance for a set of numbers. The script provides step-by-step instructions for performing these calculations, including finding the mean, calculating squared differences, and applying the correct formula.
💡Squared Differences
Squared differences are the results of subtracting the mean from each data point and then squaring the result. This concept is fundamental to the calculation of standard deviation and variance, as it quantifies the deviation of each data point from the mean in a way that is not affected by the sign of the difference. In the video, squared differences are used in the formulas for both population and sample standard deviations, as well as in the calculation of variance.
Highlights

The video explains how to calculate the standard deviation of a set of numbers, which is a statistical measure of the amount of variation or dispersion in a set of values.

Two formulas are introduced for calculating standard deviation: one for the population and one for a sample of the population.

The population standard deviation formula involves the sum of the differences between each data point and the population mean, squared and divided by the total number of data points, followed by the square root of the result.

The sample standard deviation formula is similar to the population standard deviation formula but divides by 'n-1' instead of 'n', where 'n' is the number of data points in the sample.

An example is provided to compare the standard deviation of two sets of numbers: 4, 5, 6 and 3, 5, 7.

The concept of standard deviation is explained as a measure of how far apart the numbers are from each other, with a greater spread indicating a higher standard deviation.

A visual representation of the two sets of numbers on a number line is used to illustrate the concept of standard deviation, showing that 3, 5, and 7 are more spread out than 4, 5, and 6.

The mean of the set 3, 5, 7 is calculated to be 5, and the standard deviation is calculated using the formula, resulting in a value of approximately 1.63.

The mean of the set 4, 5, 6 is also calculated to be 5, and the standard deviation for this set is calculated to be approximately 0.816.

The standard deviation for the set 3, 5, 7 is higher than for the set 4, 5, 6, which is attributed to the numbers being further apart from the mean.

The concept of variance is introduced as the square of the standard deviation, providing a measure of dispersion without the units being in standard deviation.

The formula for variance is the sum of the squared differences between each data point and the population mean, divided by the number of data points.

The video provides a step-by-step guide on how to calculate both population and sample standard deviations, as well as variance.

The video also offers resources for further learning, including a channel and a website with playlists on various subjects such as algebra, pre-calculus, calculus, chemistry, and physics.

The video concludes by summarizing the key points covered, reinforcing the understanding of standard deviation and variance calculations.

Transcripts

Browse More Related Video

Statistics: Standard deviation | Descriptive statistics | Probability and Statistics | Khan Academy

Variance and Standard Deviation With Microsoft Excel - Descriptive Statistics

Standard Deviation and Variance

Standard Error of the Mean: Concept and Formula | Statistics Tutorial #6 | MarinStatsLectures

How To Calculate The Standard Deviation

Variance and Standard Deviation: Why divide by n-1?

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsStatisticsStandard DeviationVarianceData AnalysisTutorialEducational ContentNumerical ConceptsEducation ChannelMath Video