Kinematics In One Dimension - Physics
TLDRThe video script delves into the fundamentals of kinematics, focusing on the distinction between scalar and vector quantities. It explains concepts such as mass, distance, displacement, speed, velocity, and temperature, highlighting their scalar or vector nature. The script further clarifies the difference between distance and displacement, and speed versus velocity, using practical examples for better understanding. It also introduces various formulas related to constant speed and acceleration, illustrating their application with detailed examples, emphasizing the importance of unit consistency in calculations.
Takeaways
- 📏 Kinematics describes the motion of objects without reference to force, focusing on one-dimensional motion along the x-axis and also touches on two-dimensional motion including projectile motion.
- 📌 The difference between scalar and vector quantities is that scalars have only magnitude (e.g., mass, distance), while vectors have both magnitude and direction (e.g., displacement, velocity).
- 📐 Displacement is a vector quantity that considers both the distance an object travels and the direction, whereas distance is a scalar quantity that does not account for direction.
- 🏃 Speed is a scalar quantity that indicates how fast an object is moving, whereas velocity is a vector quantity that includes both speed and direction.
- 🌡️ Temperature is a scalar quantity because it only has magnitude and no direction, although it can have negative values in certain units like Fahrenheit and Celsius.
- 🚀 Acceleration is a vector quantity that describes the rate of change of velocity, having both magnitude and direction.
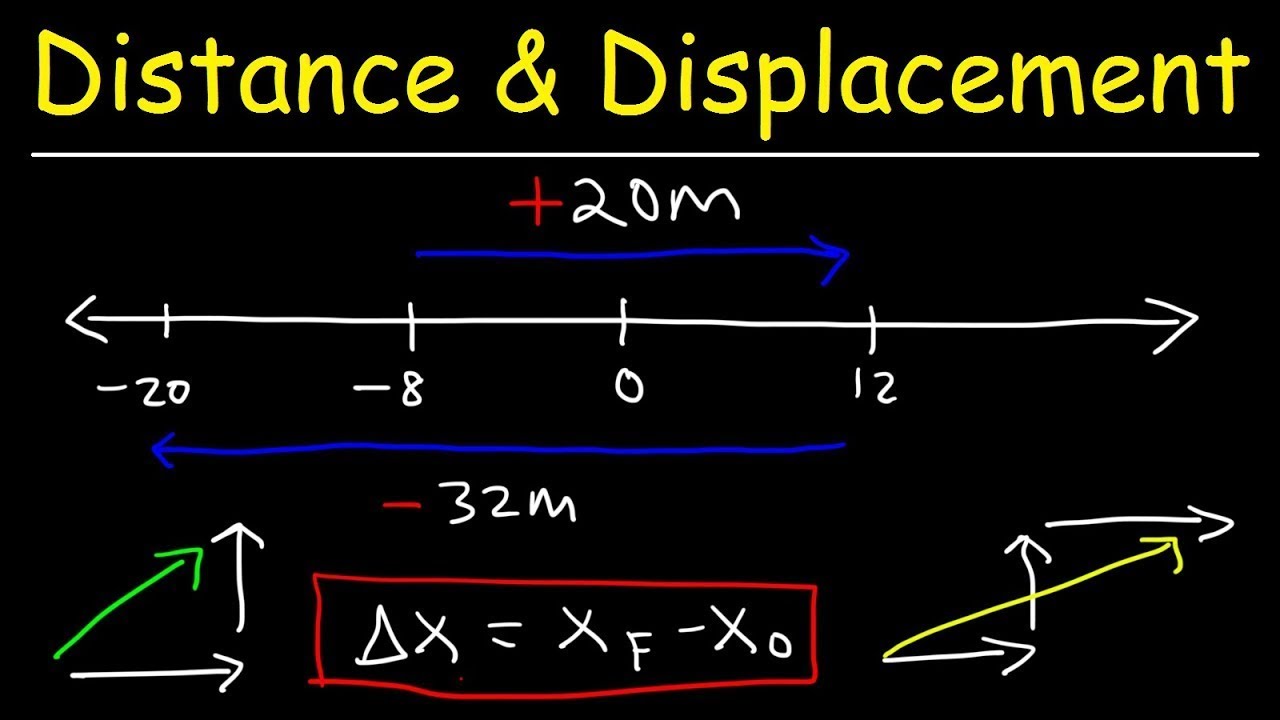
- 📈 The difference between distance and displacement is illustrated with an example where a person travels east and then west, resulting in a total distance of 17 meters but a displacement of 9 meters east.
- 📊 Average speed is calculated as the total distance traveled divided by the time elapsed, and it is always positive. In contrast, average velocity is displacement over time and can be positive or negative depending on direction.
- 🔢 For constant speed motion, the formula d = vt is used, where d represents distance or displacement, and v can be speed or velocity if the context is clear.
- 🌟 For constant acceleration motion, key formulas include d = v_bar * t, v_final = v_initial + a * t, and x_final = x_initial + v_initial * t + 0.5 * a * t^2.
- 🚌 A practical example of calculating average velocity is given, where a bus travels from a position east of a city to a position west of the city, resulting in a negative average velocity indicating the direction of travel.
Q & A
What is the main focus of the video?
-The main focus of the video is to discuss kinematics, specifically in one dimension along the x-axis, and the differences between scalar and vector quantities.
How does the video differentiate between scalar and vector quantities?
-The video differentiates scalar and vector quantities by stating that scalar quantities have only magnitude, such as mass and temperature, while vector quantities have both magnitude and direction, like displacement and velocity.
What is the definition of displacement?
-Displacement is defined as the change in position of an object, taking into account both the distance and direction of the movement.
How is speed related to velocity?
-Speed is the scalar quantity that describes how fast an object is moving, while velocity is the vector quantity that includes both the speed and the direction of the object's movement.
Can you provide an example to illustrate the difference between distance and displacement?
-An example would be a person traveling 30 meters east and then 4 meters west. The total distance traveled is 34 meters, but the displacement is 26 meters west, indicating both the magnitude and direction of the net movement.
What is the formula for calculating displacement when an object is moving with constant speed?
-The formula for calculating displacement with constant speed is d = vt, where d represents displacement, v is the constant velocity, and t is the time.
How does the video explain the calculation of average speed and average velocity?
-Average speed is calculated as the total distance traveled divided by the time elapsed. Average velocity, on the other hand, is calculated as the displacement over time. The video emphasizes that average speed is always positive, while average velocity can be positive or negative depending on the direction of movement.
What are the key formulas introduced for constant acceleration?
-For constant acceleration, the key formulas introduced are: d = v_bar * t (displacement), v_final = v_initial + a * t (final velocity), and the rearranged formula for final position: x_final = x_initial + v_initial * t + 0.5 * a * t^2.
How does the video address the concept of instantaneous speed?
-Instantaneous speed is described as the absolute value of instantaneous velocity, which tells you the velocity at a specific instant in time. It is calculated using limits, essentially as the displacement over an infinitesimally small change in time.
What is the significance of understanding the difference between distance and displacement in kinematics?
-Understanding the difference between distance and displacement is crucial in kinematics because distance is a scalar quantity that only considers the magnitude of movement, while displacement is a vector quantity that includes both magnitude and direction, which is essential for accurately describing an object's change in position.
How does the video handle negative values in scalar quantities?
-The video explains that while most scalar quantities are always positive, there are exceptions like temperature, which can have negative values depending on the units used (e.g., Fahrenheit or Celsius), but not Kelvin.
Outlines
📚 Introduction to Kinematics
This paragraph introduces the concept of kinematics, which describes the motion of objects without considering the forces involved. It focuses on one-dimensional motion along the x-axis and briefly mentions two-dimensional kinematics, including projectile motion. The distinction between scalar and vector quantities is explained, using mass, distance, and displacement as examples. The paragraph emphasizes that scalar quantities have magnitude but no direction, while vectors have both magnitude and direction. It also touches on the concept of temperature as a scalar quantity and acceleration as a vector quantity.
📏 Calculating Distance and Displacement
This section delves into the calculation of distance and displacement, using a hypothetical scenario of a person traveling east and then west. It explains that distance is the total path length traveled, always a positive scalar quantity, while displacement takes into account both magnitude and direction, resulting in a vector quantity. The example illustrates how to calculate the net displacement by considering the direction of travel. The paragraph also discusses the exception of temperature having negative values in certain units, unlike other scalar quantities.
🏃♂️ Understanding Speed vs. Velocity
This paragraph distinguishes between speed and velocity, clarifying that speed is a scalar quantity that describes how fast an object is moving without direction, while velocity is a vector quantity that includes both speed and direction. The example given involves calculating average speed and average velocity for a particle that travels east and then west, highlighting the difference between the two quantities. The paragraph emphasizes that average speed and velocity are not the same when there is a change in direction, and introduces the concept of instantaneous speed and velocity.
📝 Kinematic Equations
This section presents various kinematic equations used to describe motion with constant speed and constant acceleration. It explains the formulas for calculating displacement, average velocity, and final position in both scenarios. The paragraph also discusses the importance of using the correct units and the relationship between displacement and distance. It introduces the concept of instantaneous velocity and provides the formula for calculating it, as well as the relationship between displacement and the change in position over time.
🚌 Bus Travel Time and Average Velocity Calculation
This paragraph applies the previously discussed concepts to a real-world problem involving a bus traveling at a constant speed. It outlines the steps to convert the bus's speed from meters per second to miles per hour and then uses the formula for constant speed to calculate the time it takes to travel a certain distance. The paragraph also addresses the calculation of average velocity for a bus moving between two positions, emphasizing the importance of considering direction when calculating displacement and average velocity.
Mindmap
Keywords
💡Kinematics
💡Scalar Quantity
💡Vector Quantity
💡Displacement
💡Speed
💡Velocity
💡Temperature
💡Acceleration
💡Distance
💡Average Speed
💡Average Velocity
Highlights
Kinematics describes the motion of objects without reference to force.
The difference between scalar and vector quantities is that scalars have only magnitude, while vectors have both magnitude and direction.
Mass is a scalar quantity, while displacement is a vector quantity.
Displacement is the change in position of an object and can be described as distance with direction.
Speed is a scalar quantity, whereas velocity is a vector quantity.
Temperature is a scalar quantity as it does not involve direction.
Acceleration is a vector quantity that describes how quickly velocity changes.
Distance is always positive, while displacement can be positive or negative depending on direction.
Average speed is calculated as the total distance traveled divided by the time elapsed.
Average velocity is calculated as displacement over time and can be positive or negative.
Instantaneous speed is the absolute value of instantaneous velocity, which is the velocity at a specific instant in time.
When an object moves with constant speed, the formula d = vt is used, where d represents distance or displacement.
For constant acceleration, the displacement formula d = v_bar * t is used, where v_bar is the average velocity.
The final position formula x_final = x_initial + v_initial * t + 0.5 * a * t^2 is used for constant acceleration.
The kinematic equations can be applied along both the x-axis and y-axis for different types of motion.
When solving problems, it's crucial to ensure that units match; if not, conversion is necessary.
The example of a bus traveling at a constant speed and the calculation of the time taken to cover a certain distance illustrates the use of the d = vt formula.
Calculating the average velocity of the bus involved determining the displacement and dividing by the time interval.
Unit conversion is essential in problems involving different units of measurement, such as meters per second to miles per hour.
Understanding the difference between distance and displacement, as well as speed and velocity, is fundamental in kinematics.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: