Variance and Standard Deviation With Microsoft Excel - Descriptive Statistics

The Organic Chemistry Tutor
27 Jan 201919:17
EducationalLearning
32 Likes 10 Comments

TLDRThe video describes how to calculate the variance and standard deviation of a set of numbers. It compares two data sets and explains that standard deviation measures how spread out data are from the mean. The presenter steps through calculations for sample variance and standard deviation using the sum of squared deviations divided by N-1. For data sets with repeated values, frequency is incorporated in the calculations. The video concludes by verifying the calculations in Excel, noting that a data set with a wider spread of values has a higher standard deviation.

Takeaways
  • 😀 The variance and standard deviation measure how spread out data is from the center (mean)
  • 👉 Higher standard deviation = more variation in the data
  • ✏️ To calculate variance: Sum of squared deviations / (n - 1)
  • ✏️ To calculate standard deviation: Square root of the variance
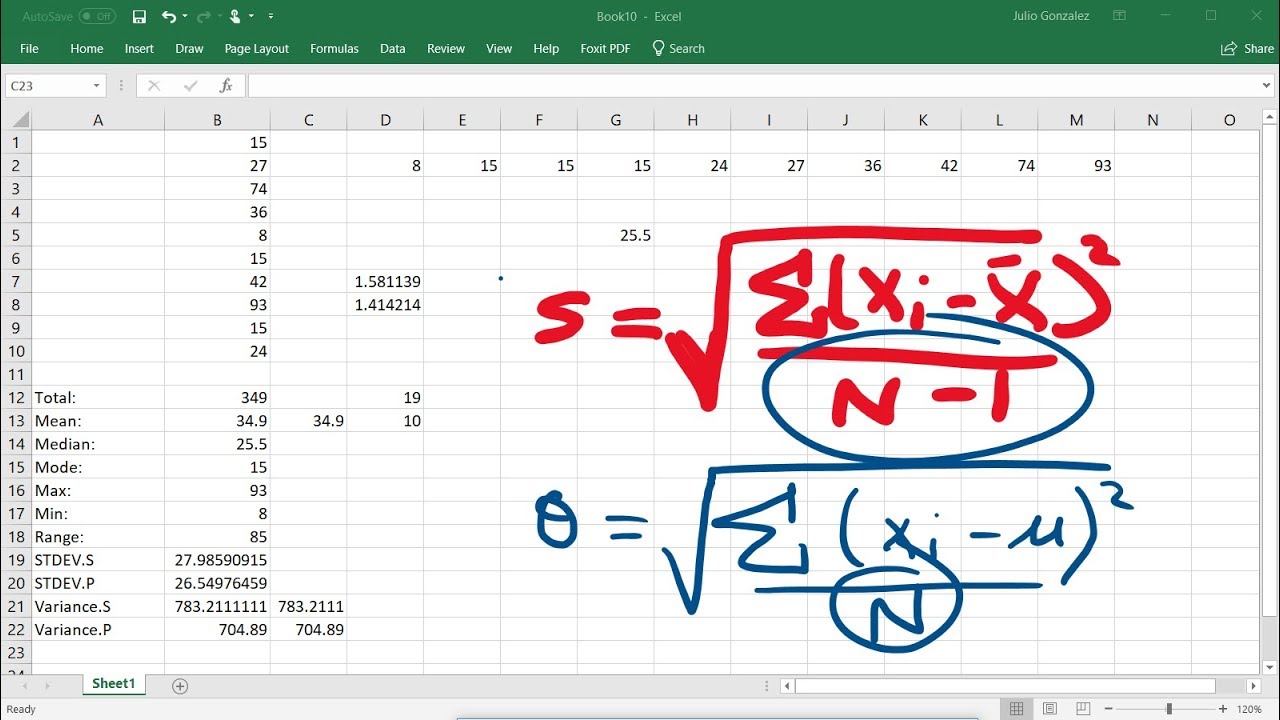
  • 📊 Can make a table with columns for: x, x̄, x - x̄, (x - x̄)2
  • 🔢 Sum x values to get the mean x̄
  • 🔢 Deviations x - x̄ should sum to 0
  • 📈 With repeating numbers, incorporate frequency in calculations
  • 💻 Can use Excel VAR.S and STDEV.S functions to calculate
  • 📊 Excel matches hand calculated variance and standard deviation
Q & A

  • What do variance and standard deviation measure?

    -Variance and standard deviation measure how far out or spread out the data values are from the mean or center.

  • Why does the second data set have a higher standard deviation than the first?

    -The second data set has numbers that differ more from the mean than the first set. For example, 10 is 2 units from the mean and 12 is 4 units. This greater spread indicates more variation.

  • How is sample variance calculated?

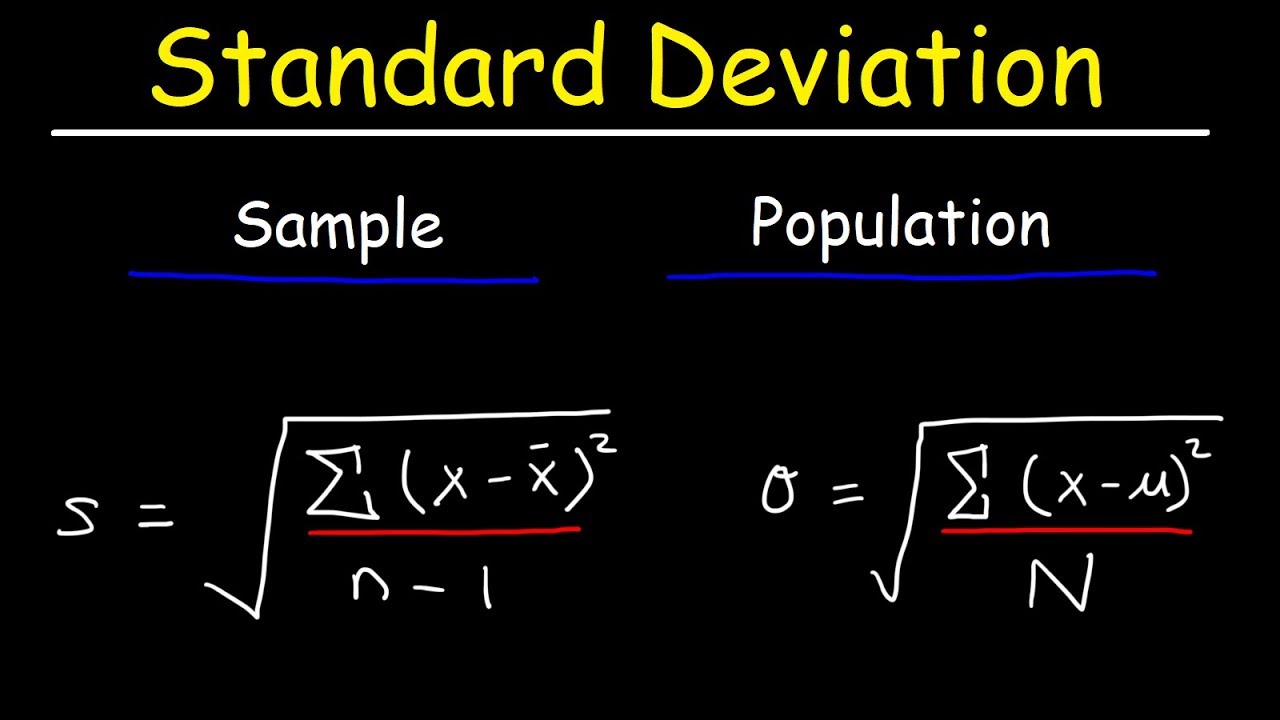
    -Sample variance is calculated by taking the sum of the squared deviations divided by n-1, where n is the number of data values.

  • What is the relationship between variance and standard deviation?

    -Standard deviation is the square root of the variance. So variance measures the average squared deviation, while standard deviation measures the average deviation.

  • Why do we sum the squared deviations?

    -By squaring the deviations before summing, negative and positive deviations do not cancel out. This allows us to measure the spread.

  • What does frequency represent in the data?

    -Frequency represents the number of times a data value occurs. For example, if 5 occurs 4 times, the frequency of 5 is 4.

  • How are calculations adjusted for frequency?

    -We multiply each data value by its frequency when finding the sum. For squared deviations, we multiple the deviations by the frequencies before summing.

  • What is n-1 in the variance formula?

    -The n-1 makes the formula calculate sample instead of population variance. It creates an unbiased estimate for the sample's true variance.

  • How can Excel calculate standard deviation?

    -Excel has predefined functions like VAR.S and STDEV.S for variance and standard deviation. Just input the data range after these to get the values.

  • What does Excel output confirm?

    -The Excel output matches our hand calculated values, helping to validate the methodology used.

Outlines
00:00
😀 Defining variance and standard deviation

This paragraph introduces the concepts of variance (s^2) and standard deviation (s), which measure how spread out data is from its center or mean. It provides an example comparing two data sets to illustrate which has a higher standard deviation based on the deviations from the mean.

05:00
😃 Calculating variance and standard deviation

This paragraph explains the step-by-step process for calculating the variance and standard deviation. It involves constructing a table with the data values, mean, deviations from the mean, squared deviations, and sums. The formulas for variance and standard deviation are provided.

10:02
😊 Incorporating frequency into variance/standard deviation calculations

This paragraph handles a more complex data set with repeating values by modifying the variance/standard deviation calculation approach. It incorporates frequency columns in the table to accurately sum the values. The process for finding the totals and plugging them into the variance and standard deviation formulas is covered.

15:03
📉 Using Excel to calculate variance and standard deviation

This final paragraph demonstrates how to utilize Excel's built-in functions to easily calculate the variance and standard deviation for the three data sets covered previously. It validates that the Excel outputs match what was calculated manually.

Mindmap
Keywords
💡variance
The variance measures how far the data points are spread out from the mean. It is used along with standard deviation to quantify the amount of variation in a data set. In the video, variance is denoted as s^2 and is calculated by summing the squared deviations divided by n-1.
💡standard deviation
Standard deviation measures how dispersed the data is in relation to the mean. It is represented by the symbol s and calculated by taking the square root of the variance. A higher standard deviation indicates the data points are more spread out from the average.
💡mean
The mean, also called the average, is calculated by summing all the data values and dividing by the total number of values n. It represents the central tendency of the data.
💡deviation
A deviation refers to how far a data point is from the mean. It is calculated by subtracting the mean from each data value. The deviations are squared and summed to find the variance.
💡frequency
Frequency refers to how often a data value occurs. When values repeat, incorporating frequency helps accurately calculate variance and standard deviation.
💡square of deviations
This involves squaring each deviation from the mean. The squared deviations help calculate variance as their sum equals the squared differences from the mean.
💡sample variance
The sample variance, denoted s^2, measures how spread out sample data is from the mean. It divides the sum of squared deviations by n-1 rather than just n.
💡population variance
Population variance is denoted as VAR.P in Excel. Unlike sample variance, population variance divides the sum of squared deviations by the total number n rather than n-1.
💡spread
Spread refers to how dispersed the data points are. Standard deviation and variance measure the spread - a wider spread means more variation.
💡Excel formulas
The video shows Excel formulas like =VAR.S and =STDEV.S to easily calculate sample variance and standard deviation for a dataset.
Highlights

Variance and standard deviation measure how spread out data is from the center

Higher standard deviation means more variation in the data values

Steps to calculate sample variance: 1) Find mean 2) Calculate deviations 3) Square the deviations 4) Sum and divide by n-1

Sample standard deviation is the square root of the sample variance

Incorporating frequency when numbers repeat simplifies calculations

Multiply frequency by squared deviations before summing for variance with repeats

Excel VAR.S and STDEV.S functions calculate sample variance and standard deviation

Higher standard deviation means data values are further from the mean

Variance measures how far data is spread from center

Deviations always sum to 0 when multiplied by frequencies

In Excel, highlight data range inside VAR.S() and STDEV.S()

Sample variance is sum of squared deviations divided by n-1

Standard deviation is square root of variance

Frequencies represent number of times each value appears

Need to multiply values by frequencies when calculating mean

Transcripts

Browse More Related Video

Calculating The Standard Deviation, Mean, Median, Mode, Range, & Variance Using Excel

Range, variance and standard deviation as measures of dispersion | Khan Academy

Statistics: Standard deviation | Descriptive statistics | Probability and Statistics | Khan Academy

Measures of Dispersion (Ungrouped Data) | Basic Statistics

Mean, Variance, and Standard Deviation of Discrete Random Variable-TI-84

Standard Deviation Formula, Statistics, Variance, Sample and Population Mean

Rate This

5.0 / 5 (0 votes)

Thanks for rating: