Normal Force Physics Problems With Tension, Inclined Planes & Free Body Diagrams
TLDRThis educational video script delves into the concept of normal force, explaining how it relates to an object's weight when resting on a surface. It illustrates how the normal force can be calculated, and how it changes when external forces are applied, such as pressing down or pulling up on the object. The script also introduces the impact of inclined surfaces on normal force, using clear examples and mathematical explanations to enhance understanding of the principles of physics involved.
Takeaways
- 📚 The normal force is the upward force exerted by a surface on an object resting on it, perpendicular to the surface.
- 🔢 For a flat object on a horizontal surface, the normal force equals the weight of the object, which is calculated as mass (m) times gravitational acceleration (g).
- 🤲 Pressing down on an object with an additional force increases the normal force, as the surface must counteract both the weight and the applied downward force.
- 🔝 Applying an upward force (e.g., pulling with a rope) decreases the normal force, as the surface supports less of the object's weight.
- 🎯 When an object is at rest, the net force is zero. The normal force equals the weight force in the absence of other forces.
- 📐 To calculate the normal force, identify all forces acting on the object in the y-direction and set up an equation based on the net force being zero (for a resting object).
- 🔢 For an object on a horizontal surface, the normal force is calculated as the object's weight (mg).
- 🔢 If a downward force is applied, the normal force is the sum of the weight force and the applied downward force (mg + F).
- 🔢 If an upward force is applied, the normal force is the difference between the weight force and the applied upward force (mg - T).
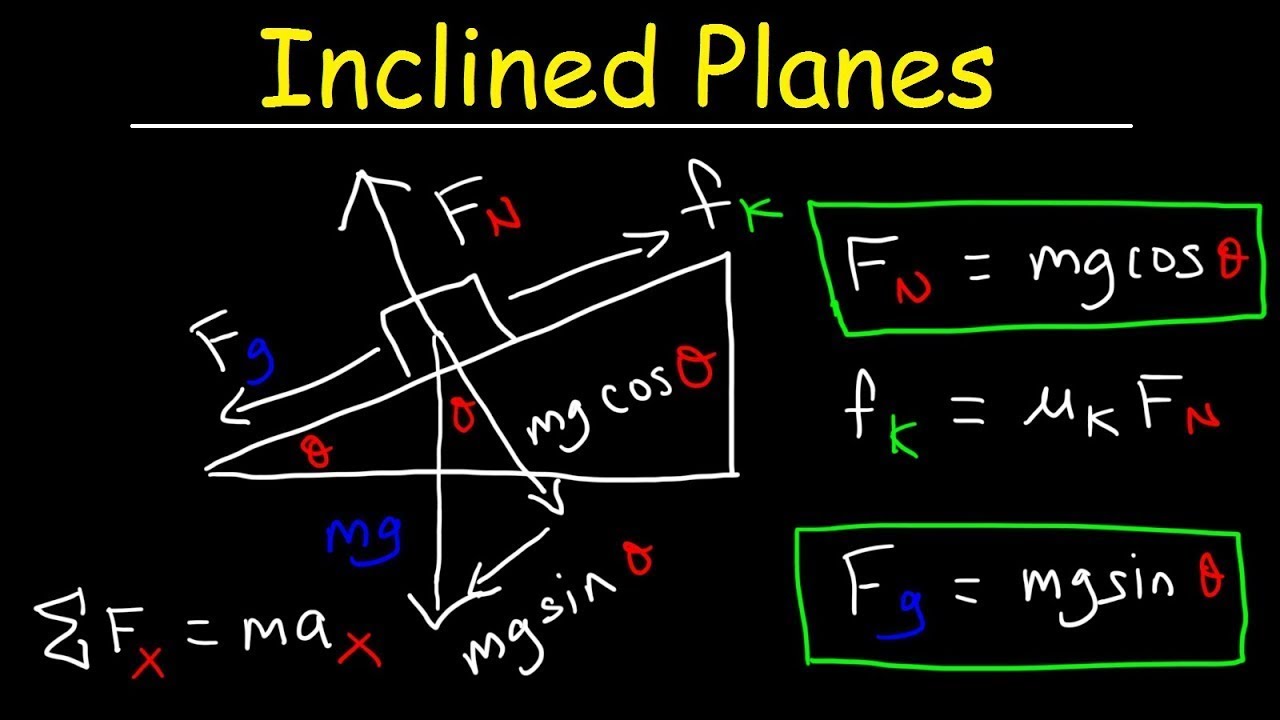
- 📐 For an object on an inclined plane, the normal force is calculated as the product of the object's weight (mg) and the cosine of the incline angle (mg * cosθ).
- 🚫 A negative result for the normal force indicates that the object is no longer in contact with the surface, as the applied force (tension or otherwise) exceeds the weight force.
Q & A
What is the normal force acting on a 5 kg box resting on a horizontal surface?
-The normal force is the weight of the object, which is calculated as mass times the gravitational acceleration (mg). For a 5 kg box, the normal force is 5 kg * 9.8 m/s^2, which equals 49 Newtons.
How can you increase the normal force without changing the mass of the object?
-You can increase the normal force by applying a downward force on the object. For example, if you press down on the block with a force of 30 Newtons, the normal force increases to counteract both the weight of the block and the applied downward force, resulting in a total normal force of 79 Newtons.
How can you decrease the normal force on an object?
-You can decrease the normal force by applying an upward force, such as pulling on a rope attached to the object. This reduces the weight the surface needs to support, thus lowering the normal force.
What is the formula for calculating the normal force when an object is at rest on a horizontal surface?
-The normal force (Fn) when an object is at rest on a horizontal surface is equal to the weight force (W), which is the mass (m) times the gravitational acceleration (g). So, Fn = mg.
What happens to the normal force when a 15 kg mass is subjected to a downward force of 100 Newtons?
-The normal force in this case is the sum of the weight force and the applied downward force. So, Fn = mg + F (where F is the applied force). For a 15 kg mass, the normal force would be 15 kg * 9.8 m/s^2 + 100 N = 147 N + 100 N = 247 Newtons.
If a 20 kg mass is pulled upwards with a tension force of 100 Newtons, how do you calculate the normal force?
-The normal force is the difference between the weight force and the tension force. Using the formula Fn = W - T (where T is the tension force), the normal force for a 20 kg mass would be Fn = (20 kg * 9.8 m/s^2) - 100 N = 196 N - 100 N = 96 Newtons.
What does a negative value for the normal force indicate?
-A negative value for the normal force indicates that the object is no longer in contact with the surface. This means the applied force (like tension) exceeds the weight force, causing the object to lift off the ground, and thus, there is no normal force acting on the object.
How do you calculate the normal force when a 30 kg block is pulled at an angle with a tension force of 300 Newtons?
-The normal force is calculated by taking the weight force and subtracting the vertical component of the tension force (tension force times sine of the angle). For a 30 kg block with a 300 N force at a 30-degree angle, Fn = mg - T_y (where T_y is the vertical component of tension). So, Fn = (30 kg * 9.8 m/s^2) - (300 N * sin(30 degrees)) = 294 N - 150 N = 144 Newtons.
What is the relationship between the normal force and the angle of inclination when an object rests on a slope?
-The normal force on an object resting on an inclined plane is given by the formula Fn = mg * cos(theta), where m is the mass of the object, g is the gravitational acceleration, and theta is the angle of inclination with respect to the horizontal.
How does the normal force change when the angle of inclination increases?
-As the angle of inclination increases, the normal force decreases because it is directly proportional to the cosine of the angle. For example, at a 60-degree angle, the normal force is half the weight of the object because cos(60 degrees) is 0.5.
What is the significance of the normal force in equilibrium situations?
-In equilibrium situations, where an object is at rest or moving with constant velocity, the normal force is crucial in balancing the forces acting on the object. It ensures that the vertical forces cancel out, maintaining the object's state of equilibrium.
Why is it important to understand the concept of normal force in physics?
-Understanding the concept of normal force is important because it helps in analyzing the forces acting on an object, especially in contact with a surface. It is essential for solving problems involving statics and dynamics, and it is a fundamental concept in the study of mechanics.
Outlines
📐 Understanding Normal Force
This paragraph introduces the concept of normal force, explaining how it acts on an object resting on a horizontal surface. It uses the example of a 5 kg box to illustrate that the normal force is equal to the weight of the object (mg). The paragraph further explores how applying additional forces, either pressing down or pulling up on the object, can alter the normal force without changing the object's mass. The key takeaway is that the normal force is the surface's response to the weight of the object and any additional forces applied to it.
🧮 Calculating Normal Force
The second paragraph delves into the mathematical aspect of calculating the normal force. It emphasizes identifying forces acting in the y-direction and setting up an equation for net force. The paragraph explains that when an object is at rest, the net force is zero, and the normal force equals the weight force (mg). It provides an example with a 10 kg object to demonstrate how to set up an equation and calculate the normal force, which in this case is 98 newtons. The paragraph also introduces the concept of applying a downward force and shows how to derive and calculate the normal force in such a scenario.
🔄 Varying Normal Force with Tension
This paragraph discusses the effect of an upward force, represented as tension (T), on the normal force. It explains how the normal force can be decreased by applying an upward force through a rope. The paragraph provides a step-by-step guide on how to write an expression for the normal force when tension is involved and how to calculate it. An example with a 20 kg mass and a 100 N tension force is used to illustrate the concept, resulting in a normal force of 96 N. The paragraph also touches on the possibility of the object lifting off the ground if the tension force exceeds the weight force, indicating that the normal force would be zero in such a case.
📐 Normal Force on an Incline
The final paragraph extends the discussion to calculate the normal force when an object rests on an inclined plane. It introduces the formula for normal force in such a scenario, which is mg cosine(theta), where theta is the angle of inclination. The paragraph explains how the normal force changes based on the angle of the incline and provides examples for horizontal and 60-degree inclined surfaces. It concludes by reinforcing that the normal force is the product of the object's weight and the cosine of the incline's angle when no other forces are acting perpendicular to the surface.
Mindmap
Keywords
💡Normal Force
💡Weight Force
💡Gravitational Acceleration
💡Free Body Diagram
💡Equilibrium
💡Tension Force
💡Incline
💡Force Components
💡Frictional Force
💡Acceleration
💡Cosine and Sine
Highlights
Calculating the normal force of an object on a horizontal surface is directly related to the object's weight.
The weight force (W) is calculated using the formula W = mg, where m is the mass and g is the gravitational acceleration (9.8 m/s² on Earth).
For a 5 kg box on a horizontal surface, the normal force is 49 N (5 kg * 9.8 m/s²).
Pressing down on an object with an additional force increases the normal force as the surface must counteract both the weight and the applied force.
An upward force applied to an object, such as through a rope, decreases the normal force as the surface supports less of the object's weight.
The normal force can be increased or decreased without changing the object's mass by applying external forces.
A free body diagram is a crucial tool in physics for visualizing and calculating the forces acting on an object at rest or in motion.
When an object is at rest, the net force is zero, which simplifies the calculation of normal force on a horizontal surface to being equal to the weight force.
For a 10 kg object at rest on a horizontal surface, the normal force is 98 N (10 kg * 9.8 m/s²).
Applying a downward force of 100 N on a 15 kg object results in a normal force of 247 N (mg + applied force).
An upward force (tension) reduces the normal force, calculated as the weight force minus the tension force.
If the tension force exceeds the weight force, the object lifts off the ground, and there is no normal force.
For a 20 kg object with a 100 N upward tension force, the normal force is 96 N (W - T).
When pulling an object at an angle, the normal force is calculated by considering only the vertical component of the tension force.
The normal force on an inclined surface is given by the formula mg cosine(theta), where theta is the angle of inclination.
On a horizontal surface (theta = 0), the normal force is 100% of the weight value (cosine of 0 is 1).
For an inclined surface with an angle of 60 degrees, the normal force is 50% of the weight value (cosine of 60 is 0.5).
Understanding the concept of normal force and its relationship with applied forces is essential for solving physics problems involving statics and dynamics.
Transcripts
Browse More Related Video
Introduction to Inclined Planes

Physics - What Is a Normal Force?

College Physics 1: Lecture 17 - Weight, Apparent Weight, and Normal Force

What is a Force & Types of Forces in Physics? - Gravity, Normal Force, Contact Forces - [1-5-1]
How Many Different Types of Forces Are There In Physics?
Elevator Physics Problem - Normal Force on a Scale & Apparent Weight
5.0 / 5 (0 votes)
Thanks for rating: