Free Body Diagrams - Tension, Friction, Inclined Planes, & Net Force
TLDRThe video script offers a comprehensive guide on drawing free body diagrams for various physical scenarios. It explains the forces acting on objects in rest or motion, including weight, normal force, tension, and friction, and how to represent these forces diagrammatically. The script covers situations like a box on a table, a block hanging from a ceiling, and objects moving at constant velocity or acceleration. It also delves into more complex examples involving inclined planes and the impact of friction on the forces and acceleration of objects.
Takeaways
- 📚 Free body diagrams visually represent all forces acting on an object.
- 🎯 When an object is at rest, the net force is zero, meaning all forces are balanced.
- 🔼 The weight force (W) on an object is calculated as mass (m) times gravitational acceleration (g).
- ↕ The normal force (N) is always perpendicular to the surface an object is on and equals the weight force when at rest.
- 🔗 Tension force in a rope is an upward force that can vary depending on the situation.
- 🏃♂️ At constant velocity, the tension force equals the weight force, indicating no net force or acceleration.
- 🚀 When an object accelerates upwards, the tension force must be greater than the weight force to create an upward net force.
- 📉 An object descending with downward acceleration indicates that the weight force is greater than the tension force.
- 🛌 For an object sliding on a frictionless horizontal surface at constant speed, there are no forces in the x-direction.
- 🔄 When an object is pushed or pulled along a surface, frictional forces (static or kinetic) come into play to balance or oppose the applied forces.
- 🔄 In the presence of friction, the net force equals the applied force minus the frictional force, which determines the object's acceleration.
- 📐 The acceleration of an object on an inclined plane without friction is given by g * sin(theta).
Q & A
What is a free body diagram?
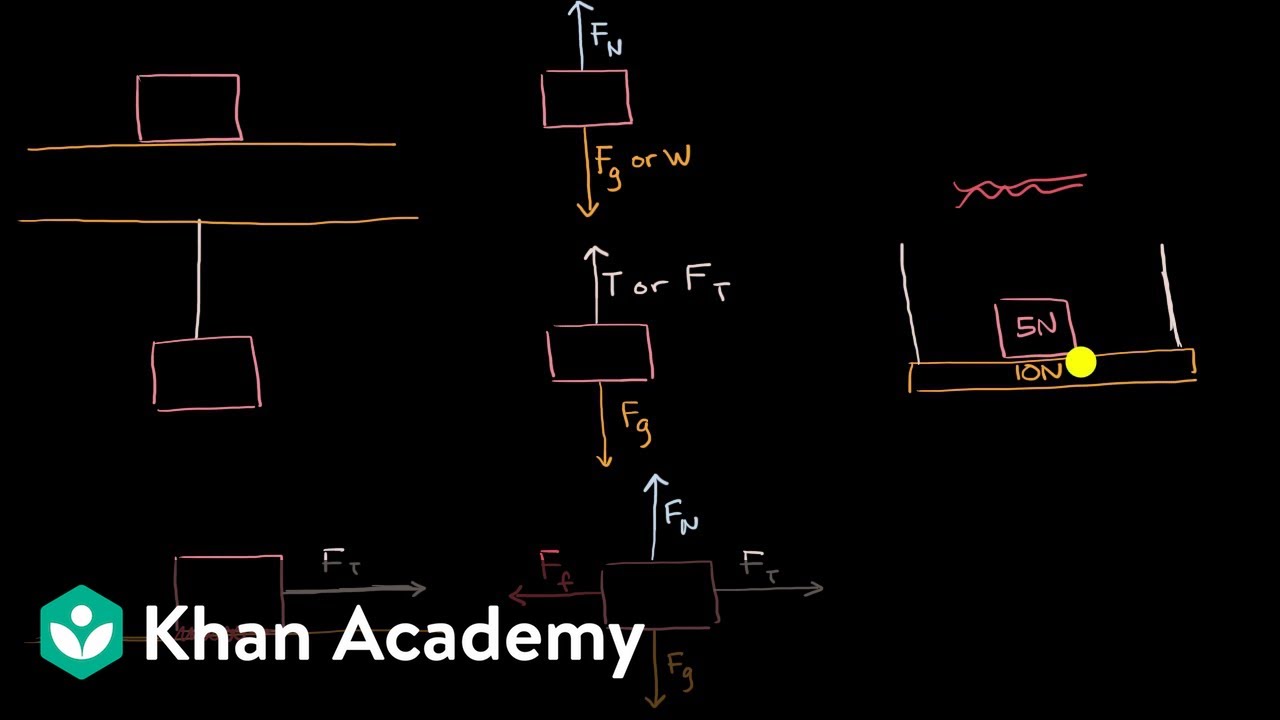
-A free body diagram is a picture that shows all of the forces acting on an object.
What forces act on a box resting on a table?
-The forces acting on a box resting on a table include the weight force (W), which is equal to the mass times the gravitational acceleration (mg), and the normal force (Fn), which is perpendicular to the surface and equal in magnitude to the weight force when the box is at rest.
How do you draw the free body diagram for a block hanging from a ceiling?
-For a block hanging from a ceiling, you draw the weight force (W) acting downward and the tension force (T) acting upward. Since the block is at rest, the tension force is equal to the weight force (T = mg).
What is the significance of the length of the arrows in a free body diagram?
-The length of the arrows in a free body diagram represents the magnitude of the forces. When two forces are equal in magnitude, their arrow lengths should be approximately the same.
How does constant velocity relate to the net force in the y direction?
-At constant velocity, the acceleration is zero, which means the net force in the y direction is also zero. This implies that the upward tension force is equal to the downward weight force, and they cancel each other out.
What happens to the tension force when a block is pulled upward with constant acceleration?
-When a block is pulled upward with constant acceleration, the tension force (T) becomes greater than the weight force (mg). The tension force is calculated as T = mg + ma, where 'a' is the acceleration.
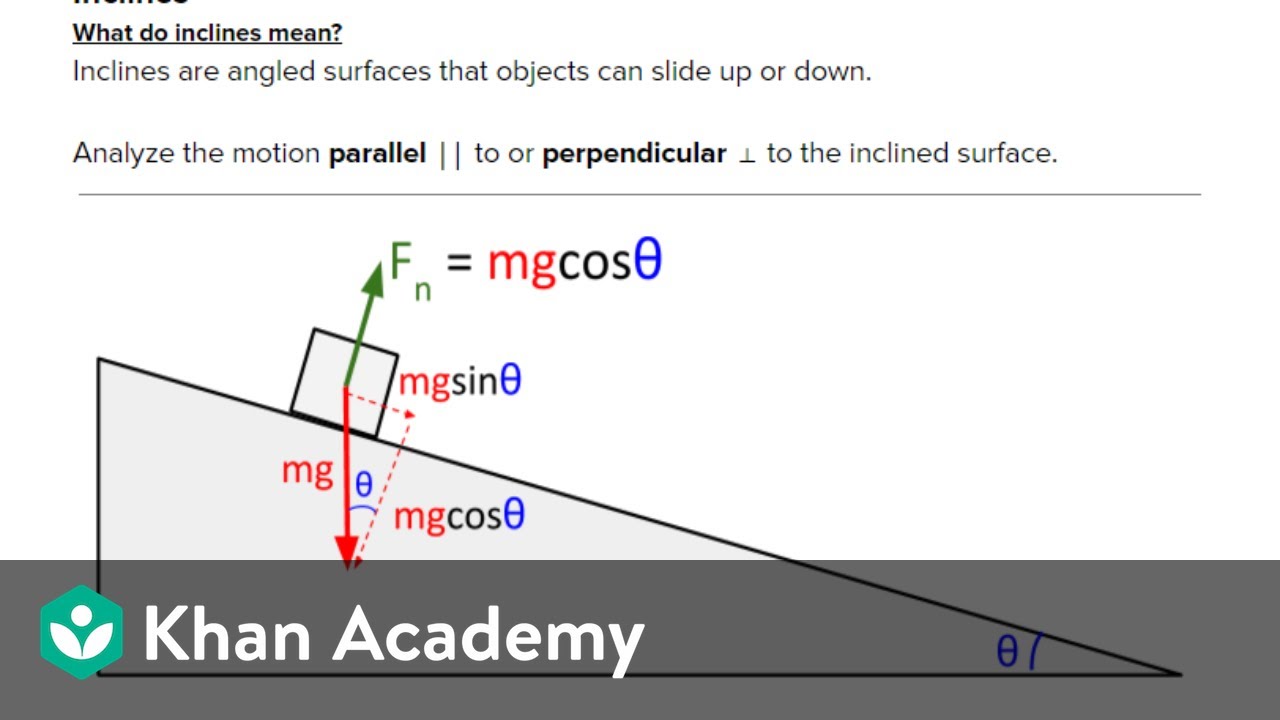
How do you calculate the normal force when a block is on an incline?
-The normal force (Fn) on an incline is calculated as Fn = mg * cosine(theta), where 'theta' is the angle of the incline.
What is the acceleration of a block sliding down a frictionless incline?
-The acceleration (a) of a block sliding down a frictionless incline is given by a = g * sine(theta), where 'g' is the acceleration due to gravity and 'theta' is the angle of the incline.
How does friction affect the forces acting on a block on an incline?
-Friction opposes motion. On an incline, static friction acts to prevent the block from sliding down when it's at rest, and kinetic friction acts when the block is sliding down the incline. The friction force is given by fk = mu_k * Fn, where 'mu_k' is the coefficient of kinetic friction and 'Fn' is the normal force.
What is the net force acting on a block when it's being pulled up an incline at constant velocity?
-When a block is being pulled up an incline at constant velocity, the net force in the x-direction is zero because the tension force (T) is equal to the kinetic friction force (fk), which is fk = mu_k * Fn.
How can you calculate the tension force when pulling a block up an incline against friction at constant velocity?
-The tension force (T) when pulling a block up an incline against friction at constant velocity is calculated as T = fk = mu_k * Fn, where 'Fn' is the normal force on the incline (mg * cosine(theta)).
Outlines
📚 Introduction to Free Body Diagrams
This paragraph introduces the concept of free body diagrams, which are used to visually represent all the forces acting on an object. It begins with a problem involving a box resting on a table, explaining the forces involved such as weight (W) and normal force. The weight force is calculated as mass (m) times gravitational acceleration (g), and on Earth, g is approximately 9.8 m/s². The normal force is described as perpendicular to the surface and equal in magnitude to the weight force when the object is at rest. The paragraph then moves on to describe free body diagrams for different scenarios, including a block hanging from a ceiling and a block moving upward at constant velocity, emphasizing the balance of forces and the importance of net force in determining the state of motion.
🚀 Dynamics of Blocks with Varying Accelerations
This section delves into the dynamics of blocks under different acceleration conditions. It starts by discussing a block being pulled upward with constant acceleration, explaining how to calculate the tension in the rope using the equation for net force (T - mg = ma). The paragraph then covers a block descending with downward acceleration, highlighting that the gravitational force exceeds the tension force in this case. Further examples include a block sliding across a frictionless surface at constant speed, where only normal and gravitational forces act, and a block pushed to the right at constant speed with an applied force, introducing the concept of kinetic friction.
🔧 Calculating Forces and Accelerations with Inclines
This paragraph focuses on calculating the forces and accelerations when a block interacts with an incline. It begins with a block sliding down a frictionless incline, explaining the forces at play and how to calculate the acceleration (a = g * sin(theta)). The paragraph then discusses a block at rest on an incline, where static friction is equal to the component of gravitational force (fg) acting down the slope. It continues with a block sliding down an incline with friction at constant acceleration, detailing the net force equation (fg - fk = ma) and how to calculate the acceleration in this context. Finally, it describes a block being pulled up an incline at constant velocity against friction, where the tension force equals the kinetic friction force.
📐 Trigonometry in Free Body Diagrams
This paragraph introduces the application of trigonometry in free body diagrams, specifically for problems involving forces at an angle. It explains how to calculate the x (Tx) and y (Ty) components of a force (T) using trigonometric functions (Ty = T * sin(theta) and Tx = T * cos(theta)). The paragraph then applies these concepts to calculate the normal force and acceleration of a block pulled at an angle across a horizontal surface. It also discusses how to find the acceleration in the x-direction using the net force equation and the components of tension force.
Mindmap
Keywords
💡Free Body Diagram
💡Weight Force
💡Normal Force
💡Tension Force
💡Constant Velocity
💡Acceleration
💡Friction
💡Incline
💡Newton's Second Law
💡Trigonometry
💡Static Friction
💡Kinetic Friction
Highlights
Introduction to free body diagrams and their importance in visualizing forces acting on an object.
Explanation of how to draw a free body diagram for a box resting on a table, including the weight force (W) and normal force (N).
Discussion on the equality of normal and weight forces when an object is at rest on a horizontal surface.
Illustration of a free body diagram for a block hanging from a ceiling, highlighting the balance between weight force and tension force.
Explanation of how to represent forces in a free body diagram when an object is moving at a constant velocity.
Description of the net force and acceleration when an object is moving upward at a constant velocity.
Demonstration of how to draw a free body diagram for a block being pulled upward with constant acceleration.
Explanation of the relationship between tension force and weight force during upward acceleration.
Discussion on the forces acting on a block descending with downward acceleration using a rope.
Introduction to free body diagrams for objects moving on a frictionless horizontal surface at constant speed.
Explanation of the forces involved when an object is pushed to the right at constant speed on a horizontal surface.
Description of the role of kinetic friction in maintaining constant speed on a horizontal surface.
Illustration of a free body diagram for a box being accelerated across a horizontal surface with friction present.
Explanation of the balance between tension force and frictional force when pulling a block at constant velocity on a horizontal surface.
Discussion on the forces acting on a block when pulled at an angle across a horizontal surface with friction.
Introduction to calculating the normal force and tension components using trigonometry and SOHCAHTOA.
Explanation of how to calculate the acceleration of a block sliding down a frictionless incline.
Description of the forces acting on a block at rest on an incline, including the role of static friction.
Calculation of the acceleration of a block sliding down an incline with friction present at constant acceleration.
Explanation of the tension force required to pull a block up an incline against friction at constant velocity.
Transcripts
Browse More Related Video
AP Physics 1 review of Forces and Newton's Laws | Physics | Khan Academy
Types of forces and free body diagrams | AP Physics 1 | Khan Academy

High School Physics - Ramps and Inclines

Master Free-Body Diagrams for Physics Problems - [1-5-18]

College Physics 1: Lecture 13 - Motion and Forces

College Physics 1: Lecture 15 - Equilibrium and Newton's Second Law
5.0 / 5 (0 votes)
Thanks for rating: