How to Solve Inclined Plane Problems
TLDRIn this informative and engaging video, Physics Ninja explores inclined plane problems, focusing on three distinct scenarios. He begins by examining the case of a block sliding down a frictionless ramp, detailing how to calculate the speed at the bottom and the time taken to reach it. The second scenario involves launching a block up the ramp with an initial velocity and determining how far it travels before stopping, accounting for friction. Lastly, an equilibrium problem is tackled, where a string attached to a block on an incline is analyzed to find the tension in the string when the block is stationary. Throughout the video, the importance of understanding force components and the correct application of Newton's laws is emphasized, providing a solid foundation for solving such physics problems.
Takeaways
- 📚 Understanding inclined plane problems involves analyzing forces such as gravity, friction, and the normal force.
- 🧱 The first problem examines a block sliding down a frictionless ramp, focusing on finding the speed at the bottom and the time taken to slide down.
- 🚀 For the second problem, with an initial velocity given, the challenge is to determine how far the block travels up the ramp before stopping, considering friction.
- ⚖️ The equilibrium problem in the third scenario involves a string tied to a block on an incline, aiming to calculate the tension in the string when the block is stationary.
- 📐 A free body diagram is essential for visualizing and solving inclined plane problems, breaking down forces into components along and perpendicular to the ramp.
- 📌 The weight of the block can be decomposed into two components: one parallel to the ramp (mg * sin(theta)) and one perpendicular (mg * cos(theta)).
- 🕒 To find the time it takes for the block to slide down, use kinematic equations and the acceleration due to gravity along the ramp.
- 🏗️ For the block sliding up, apply Newton's laws of motion, considering the forces acting along the x-direction, and use kinematic equations to find the displacement.
- 🔗 The tension in the string during equilibrium is equal to the component of the weight parallel to the ramp, calculated as mg * sin(theta).
- 📐 Trigonometry plays a crucial role in calculating distances and heights on inclined planes, using angles relative to the horizontal surface.
- 🔄 When dealing with inclined planes, it's often best to use a coordinate system with one axis along the ramp and one perpendicular to it for simplicity in calculations.
Q & A
What are the three types of inclined plane problems discussed in the transcript?
-The three types of inclined plane problems discussed are: 1) Finding the speed at the bottom and the time taken for an object to slide down a frictionless ramp, 2) Determining how far an object with an initial velocity will go before stopping when launched up a ramp with friction, and 3) Calculating the tension in a string tied to an object at equilibrium on an inclined plane.
How is the weight of the block broken down into components in the context of an inclined plane?
-The weight of the block is broken down into two components: one parallel to the ramp (mg * sin(theta)) and one perpendicular to the ramp (mg * cos(theta)). This is done using trigonometry based on the angle of inclination (theta) of the ramp.
What is the significance of choosing the right coordinate system for inclined plane problems?
-Choosing the right coordinate system simplifies the mathematical calculations. It is recommended to have at least one axis pointing along the direction of motion, which in the case of a sliding block, is typically along the ramp (x-axis) and the other axis perpendicular to the ramp (y-axis).
How is the normal force calculated in the context of an inclined plane?
-The normal force is calculated using the forces acting on the block in the vertical direction. Since the block is not moving vertically, the sum of the forces in the vertical direction must be zero. Therefore, the normal force is equal to the component of the weight acting in the y direction (mg * cos(theta)).
What is the acceleration of the block sliding down a frictionless ramp calculated to be?
-The acceleration of the block sliding down a frictionless ramp is calculated to be g * sin(theta), where g is the acceleration due to gravity and theta is the angle of inclination of the ramp.
How is the time taken for the block to slide down the ramp determined?
-The time taken is determined using the kinematic equation for time, which is derived from the equation of motion under constant acceleration. The time (t) is calculated as the square root of (2 * x / a), where x is the distance traveled down the ramp and a is the acceleration of the block.
What is the speed of the block at the bottom of the ramp calculated to be?
-The speed of the block at the bottom of the ramp is calculated using the kinematic equation for final velocity, which is the initial velocity plus acceleration times time. Since the initial velocity is zero (the block is released from rest), the final velocity is simply acceleration times time.
How does the presence of friction affect the inclined plane problem?
-The presence of friction introduces an additional force, the force of kinetic friction, which acts opposite to the direction of motion. This force, along with the component of the weight acting down the ramp, determines the new acceleration of the block, which will be less than the acceleration on a frictionless ramp.
How is the maximum height reached by the block when launched up the ramp with friction determined?
-The maximum height is determined by using the kinematic equation that relates the final velocity (which is zero at the maximum height) to the initial velocity, acceleration, and displacement. The displacement is found by rearranging the equation to solve for x, which gives the distance the block travels up the ramp before stopping.
What is the tension in the string when the block is in equilibrium on an inclined plane?
-The tension in the string when the block is in equilibrium is equal to the component of the weight acting parallel to the ramp, which is calculated as mg * sin(theta). This is because the forces in both the x and y directions must sum to zero for the block to be in equilibrium.
How does the angle of inclination affect the forces acting on the block and the resulting motion?
-The angle of inclination (theta) directly affects the components of the weight acting on the block, which in turn influences the acceleration, the time taken to slide down, and the distance traveled up the ramp. A steeper angle increases the component of weight parallel to the ramp, leading to higher acceleration and potentially greater distances traveled under gravity alone or with friction.
Outlines
📚 Introduction to Incline Plane Problems
The video begins with an introduction to physics problems involving inclined planes. The speaker, Physics Ninja, plans to discuss three types of problems related to inclined planes, focusing on forces such as gravity, friction, and the normal force. The first problem involves a block sliding down a ramp without friction, aiming to find the speed at the bottom and the time it takes to slide down. The second problem is about launching a block up the ramp with an initial velocity and determining how far it goes before stopping. The third problem is an equilibrium problem, where a string is tied to a block on an incline and connected to a wall, with the goal of finding the tension in the string when the block is stationary. The speaker emphasizes the importance of understanding how to tackle forces when dealing with an inclined plane.
📐 Analyzing Forces on an Inclined Plane
The speaker delves into the forces acting on a block resting on an inclined plane. The weight of the block is the primary force, which is decomposed into two components: one parallel to the ramp (mg * sin(theta)) and one perpendicular to the ramp (mg * cos(theta)). The normal force is also discussed, which acts perpendicular to the surface of the ramp. The speaker explains the importance of choosing a coordinate system that simplifies the problem, with one axis along the ramp and the other perpendicular to it. The video script includes a detailed explanation of how to break down the weight vector into its components using trigonometry and the significance of the angle of inclination.
🚀 Calculating Motion Down a Frictionless Ramp
The speaker presents a specific problem where a block slides down a frictionless ramp. Using Newton's laws of motion and the previously discussed force components, the speaker calculates the acceleration of the block (g * sin(theta)). The problem involves finding the time it takes for the block to travel down the ramp and the final speed at the bottom. The speaker uses kinematic equations to relate the height of the ramp, the acceleration, and the distance traveled by the block. The solution involves calculating the distance using trigonometry (height/sin(theta)) and then using the kinematic equation to find the time (2x/a) and the final speed (v = u + at), where u is the initial velocity, a is the acceleration, and t is the time.
🛑 Problem Variation: Block with Friction on Ramp
The speaker introduces a variation of the previous problem, this time including friction between the block and the ramp. The force diagram is updated to include kinetic friction, which is the product of the coefficient of kinetic friction and the normal force. The speaker applies Newton's second law to find the new acceleration of the block, which is now negative due to the direction of motion being opposite to the positive x-direction. The problem aims to find how far the block will slide up the ramp before stopping. The speaker uses the kinematic equation relating final velocity, initial velocity, acceleration, and displacement to solve for the displacement. The final displacement is negative, indicating the direction of motion is up the ramp, and the speaker calculates the distance the block will travel before coming to rest.
🔄 Equilibrium Problem with Tension on a Block
The final problem discussed involves a block on an inclined plane with a string tied to it and attached to a wall. The speaker focuses on the equilibrium condition, where the sum of forces on the block must be zero in both the x and y directions. The speaker uses the free body diagram to analyze the forces, including the weight, normal force, and tension from the string. The tension is calculated by balancing the weight component parallel to the ramp (mg * sin(theta)) with the tension force. The speaker concludes by solving for the tension using the known values for mass, gravitational acceleration, and the sine of the ramp's angle of inclination.
Mindmap
Keywords
💡Incline Plane
💡Forces
💡Free Body Diagram
💡Gravity
💡Friction
💡Normal Force
💡Tension
💡Equilibrium
💡Kinematics
💡Acceleration
💡Coordinate System
Highlights
The speaker begins by introducing the topic of incline plane problems and the three types of problems that will be discussed.
The importance of understanding how to tackle forces when dealing with an inclined plane is emphasized.
The first problem involves finding the speed at the bottom of the ramp and the time it takes for an object to slide down.
The second problem focuses on determining how far an object with an initial velocity will travel up the ramp before stopping.
The third problem is an equilibrium problem where the goal is to find the tension in a string tied to a block on an incline.
A detailed explanation of setting up a free body diagram for a block on an incline is provided.
The weight of the block is broken down into two components: one parallel to the ramp and one perpendicular.
The use of a coordinate system is discussed, with a recommendation to use one axis pointing along the direction of motion for simplicity.
The speaker provides a method for calculating the distance traveled down the ramp using trigonometry.
The time it takes for the block to travel down the ramp is calculated using kinematic equations.
The speed of the block at the bottom of the ramp is determined using the calculated time and known acceleration.
The second problem involves the addition of friction, requiring the calculation of kinetic friction and its impact on the block's motion.
The maximum height reached by the block is determined by setting the final velocity to zero in the kinematic equations.
The tension in the string for the equilibrium problem is found by analyzing the forces in the x direction and setting them equal to zero.
The speaker concludes by summarizing the process of solving incline plane problems, highlighting the importance of understanding force components and the use of coordinate systems.
Transcripts
Browse More Related Video
Work Energy Problem - Sliding Down a Ramp
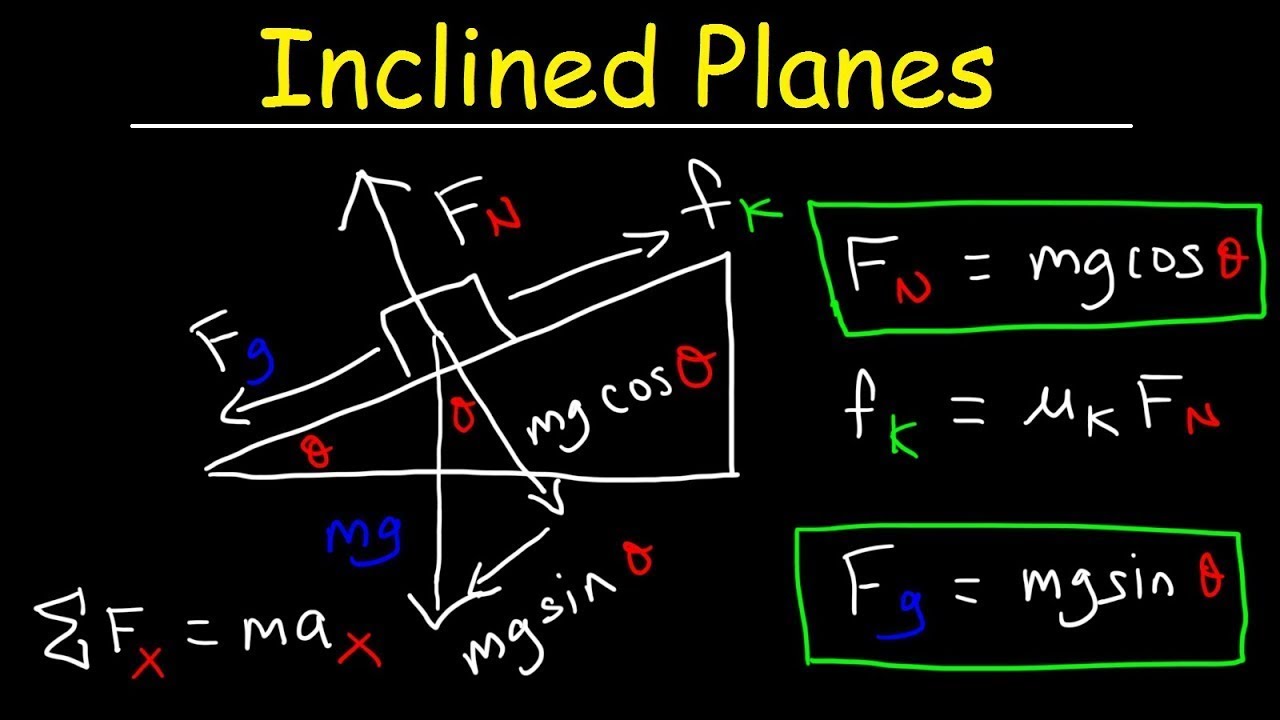
Introduction to Inclined Planes

2016 #1 Free Response Question - AP Physics 1 - Exam Solution
Newton's Second Law Exam Question: Two-body systems Pulley practice

AP Physics 1 Work and Energy Practice Problems and Solutions

Blocks Sliding Down Ramps, and All That: Physics Help Room
5.0 / 5 (0 votes)
Thanks for rating: