Limits at infinity of quotients with square roots (even power) | AP Calculus AB | Khan Academy

Khan Academy
15 Jul 201603:36
EducationalLearning
32 Likes 10 Comments

TLDRThe video script presents a mathematical approach to finding the limit of a rational expression as x approaches negative infinity. It emphasizes the importance of identifying the highest degree term and dividing both the numerator and the denominator by x to that power to simplify the expression. The example given involves a square root function, which is treated as a second-degree term due to its radical nature. Through step-by-step simplification, the limit is found to be one, illustrating the process of evaluating limits in calculus.

Takeaways
  • 🔍 The task is to find the limit as x approaches negative infinity for a given rational expression.
  • 📈 Identify the highest degree term in both the numerator and the denominator as the first step in solving the limit.
  • 📚 Divide the numerator and the denominator by x to the power of the highest degree to simplify the expression.
  • 🌟 Even though there's an x to the fourth in the numerator, it's under a square root, making it effectively a second-degree term.
  • 📝 Perform the division by x squared to transform the expression into a more manageable form.
  • 🛣️ As x approaches negative infinity, terms involving x in the denominator will approach zero.
  • 📈 The limit calculation involves assessing how the magnitude of the denominator affects the overall result.
  • 🥇 The square root of four minus one, simplified, leads to the square root of three, which is a constant.
  • 🎯 The simplified expression after dividing by x squared is the square root of three over two, which further simplifies to one.
  • 📊 Understanding the behavior of the expression as x approaches negative infinity is crucial for finding the limit.
  • 🎓 The final answer to the limit problem is one, showcasing the importance of simplifying the rational expression first.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is finding the limit of a rational expression as x approaches negative infinity.

  • How does the process of finding limits at infinity for rational expressions work?

    -To find limits at infinity for rational expressions, one should look at the highest degree term in both the numerator and the denominator, and then divide both by x raised to the power of that degree. This simplifies the expression to constants and terms that approach zero as x approaches infinity.

  • What is the specific rational expression the video is trying to evaluate?

    -The specific rational expression is the limit as x approaches negative infinity of the square root of (4x to the fourth minus x) over (2x squared plus three).

  • How does the square root of a higher degree term under a radical affect the analysis?

    -A higher degree term under a radical can be viewed as a lower degree term when considering the limit at infinity. In this case, x to the fourth under a square root is effectively treated as a second-degree term.

  • What is the step-by-step process for simplifying the given expression?

    -The process involves dividing both the numerator and the denominator by x squared, which simplifies the expression to the square root of (4 - (1/x^3)) over 2, and then further simplifying as x approaches negative infinity.

  • What happens to the terms in the numerator and denominator as x approaches negative infinity?

    -As x approaches negative infinity, the terms in the numerator and denominator approach zero because they are divided by increasingly larger negative values of x squared.

  • What is the final result of the limit as x approaches negative infinity for the given expression?

    -The final result of the limit is the square root of four over two, which simplifies to two over two, and thus equals one.

  • Why does the limit of the given expression equal one?

    -The limit equals one because the numerator simplifies to the principal square root of four minus one, which is two, and the denominator simplifies to two, resulting in a ratio of two over two, which equals one.

  • What is the significance of the limit approaching zero in this context?

    -The limit approaching zero signifies that the magnitude of x is becoming very large in the negative direction, and the expression's value is converging towards a finite number as x becomes more negative.

  • How does this video script help in understanding limits at infinity for rational expressions?

    -The video script provides a step-by-step walkthrough of a specific example, explaining the process of simplifying the expression and evaluating the limit, which helps in understanding the general approach to finding such limits.

Outlines
00:00
📚 Calculating Limits at Negative Infinity

The paragraph discusses the process of finding the limit of a rational expression as x approaches negative infinity. It emphasizes the importance of identifying the highest degree term in both the numerator and the denominator and then dividing each by x raised to the power of that degree. The example used is the limit of the square root of (4x to the fourth minus x) over (2x squared plus three) as x approaches negative infinity. The explanation details how to simplify the expression by treating the highest degree term under a square root as a second-degree term and then dividing both the numerator and the denominator by x squared. The result is a limit calculation that simplifies to the square root of four (which is two) divided by two, ultimately yielding the answer of one.

Mindmap
Keywords
💡limit
In the context of the video, 'limit' refers to a mathematical concept used to describe the value that a function or sequence approaches as the input (often denoted as 'x') approaches some value. Specifically, the video is focused on finding the limit as x approaches negative infinity for a given function. This concept is crucial for understanding the behavior of functions at extreme values and is used to predict the outcome or trend of the function's output.
💡rational expressions
Rational expressions are mathematical expressions that involve a numerator and a denominator, similar to fractions. In the video, the function given is a rational expression because it consists of a numerator (the square root of a polynomial) and a denominator (a polynomial). Rational expressions are important in calculus and algebra as they can represent a wide variety of functions, including those that have asymptotic behavior or undefined points.
💡highest degree term
The 'highest degree term' in a polynomial is the term with the greatest exponent when the polynomial is written in standard form. In the context of the video, identifying the highest degree term is crucial for simplifying the function and finding its limit at infinity. The degree of a term determines the behavior of the function as the variable grows very large or very small.
💡divide by x to the power
The phrase 'divide by x to the power' refers to the process of dividing both the numerator and the denominator of a rational expression by x raised to the power that corresponds to the highest degree term. This technique is used to simplify the expression and find its limit at infinity by reducing the higher-degree terms to lower-degree or constant terms, which makes it easier to evaluate the limit.
💡square root
A 'square root' is a mathematical operation that finds a number which, when multiplied by itself, gives the original number. In the context of the video, the square root is applied to the numerator of the function, which involves a polynomial under the radical. Understanding the behavior of square roots and how they interact with other terms in the function is essential for simplifying the expression and determining its limit.
💡infinity
In mathematics, 'infinity' is a concept representing an unbounded quantity, larger than any real number. It is not a number itself but rather a representation of a limit or endlessness. In the video, the focus is on the behavior of the function as x approaches negative infinity, which is a crucial concept in calculus for understanding the asymptotic behavior of functions.
💡constants
In mathematics, 'constants' are values that do not change. In the context of the video, when simplifying the function to find the limit, certain terms can be considered as constants because they do not depend on the variable x and will remain the same regardless of the value of x. Constants play a key role in determining the limit of a function as they do not go to zero or infinity and thus help in evaluating the function's long-term behavior.
💡asymptotic behavior
Asymptotic behavior refers to the behavior of a function as it approaches a particular value or infinity. It is often used to describe how a function grows or decreases without bound, or how it levels off to a certain value. In the video, the asymptotic behavior is relevant because it helps to predict what the function's output will do as x becomes very large in the negative or positive direction.
💡exponents
Exponents are a mathematical notation that indicate how many times a base number is multiplied by itself. They are used to express the power to which the base is raised. In the video, exponents are present in the polynomial terms of the function, and understanding how these exponents affect the function's behavior is important for simplifying the expression and finding its limit.
💡simplifying expressions
Simplifying expressions involves using mathematical rules to reduce complex expressions to a simpler form. In the context of the video, simplifying is crucial for making the function easier to understand and for finding its limit at negative infinity. By simplifying, we can remove or reduce the influence of terms that become insignificant as x grows large, allowing us to focus on the terms that dominate the function's behavior.
💡principal root
The 'principal root' is the positive root of a number when considering square roots or other even roots. In the context of the video, when discussing the square root of a number, the principal root is the non-negative solution. This concept is important because it specifies which root is being considered when the square root of a number is used in a mathematical expression.
Highlights

The problem presented involves finding a limit as x approaches negative infinity for a given rational expression.

The strategy for solving such limits involves examining the highest degree term in both the numerator and the denominator.

Dividing the numerator and denominator by the highest degree term in x simplifies the expression for limit analysis.

The expression under a square root is considered as a whole, and its degree is effectively reduced due to the radical.

The highest degree term in the given expression is of the second degree, which is the focus for the limit calculation.

Dividing the expression by x squared is the key step to simplify the expression and find the limit.

The limit process involves understanding how the magnitude of negative infinity affects the variables involved.

As x approaches negative infinity, the terms divided by x tend towards zero, simplifying the expression further.

The limit calculation results in a simple expression of the square root of four, which is a fundamental mathematical concept.

The final answer to the limit is one, a straightforward and elegant solution to the problem presented.

This method of finding limits is useful for a variety of rational expressions involving positive or negative infinity.

The approach taken in the transcript demonstrates a systematic and logical method for tackling complex mathematical problems.

The transcript provides a clear and detailed explanation, making it accessible for learners at various levels of mathematical understanding.

The use of exponent rules and simplification techniques is crucial in deriving the solution to the limit problem.

The problem-solving process outlined in the transcript can be applied to a wide range of mathematical limit scenarios.

The transcript serves as an educational tool, teaching viewers not only the specific solution but also the general approach to similar problems.

Transcripts

Browse More Related Video

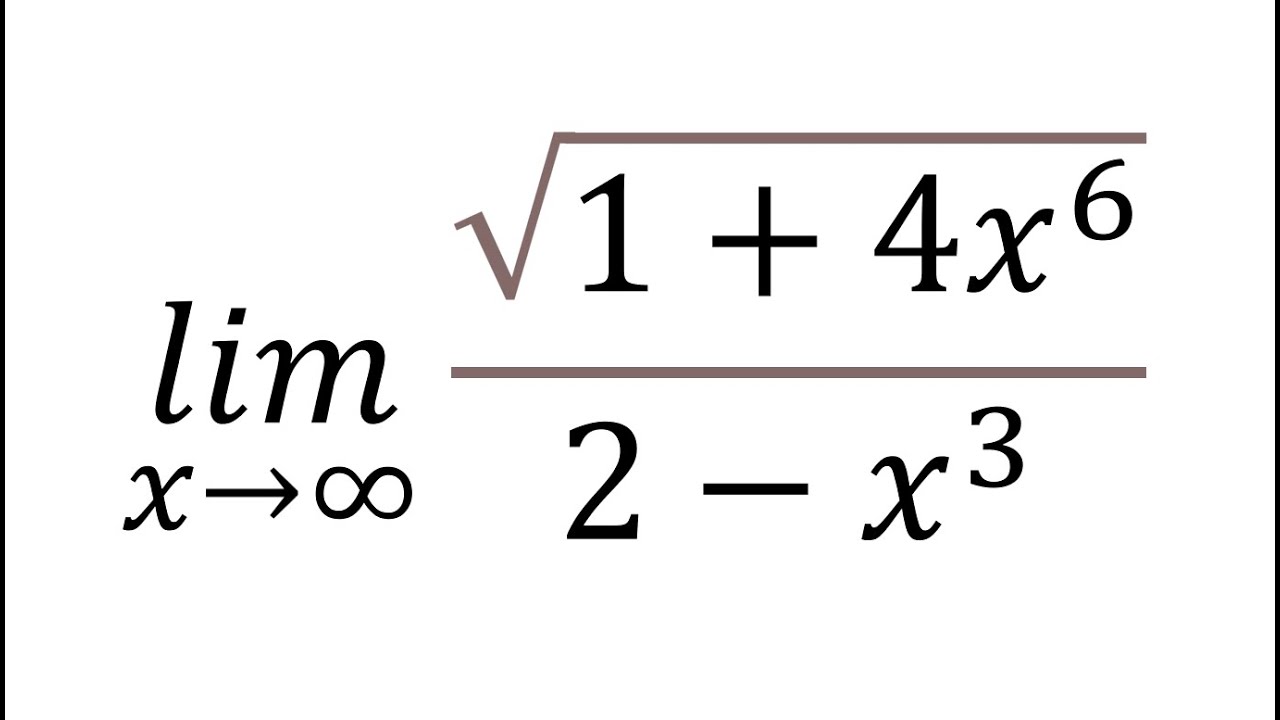
Find limit at Infinity | sqrt(1+4x^6)/(2-x^3) x approaches infinity | general solution

Limits at infinity of quotients (Part 2) | Limits and continuity | AP Calculus AB | Khan Academy

Computing Limits at Infinity for Rational Functions

Limits at Infinity With Radicals & Fractional Exponents

Example (2.2) - Finding the limit of a function #15 (Calc)

Limits at infinity of quotients (Part 1) | Limits and continuity | AP Calculus AB | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsCalculusLimitsInfinityRational FunctionsEducationalProblem SolvingMath TutorialCritical ThinkingAlgebra