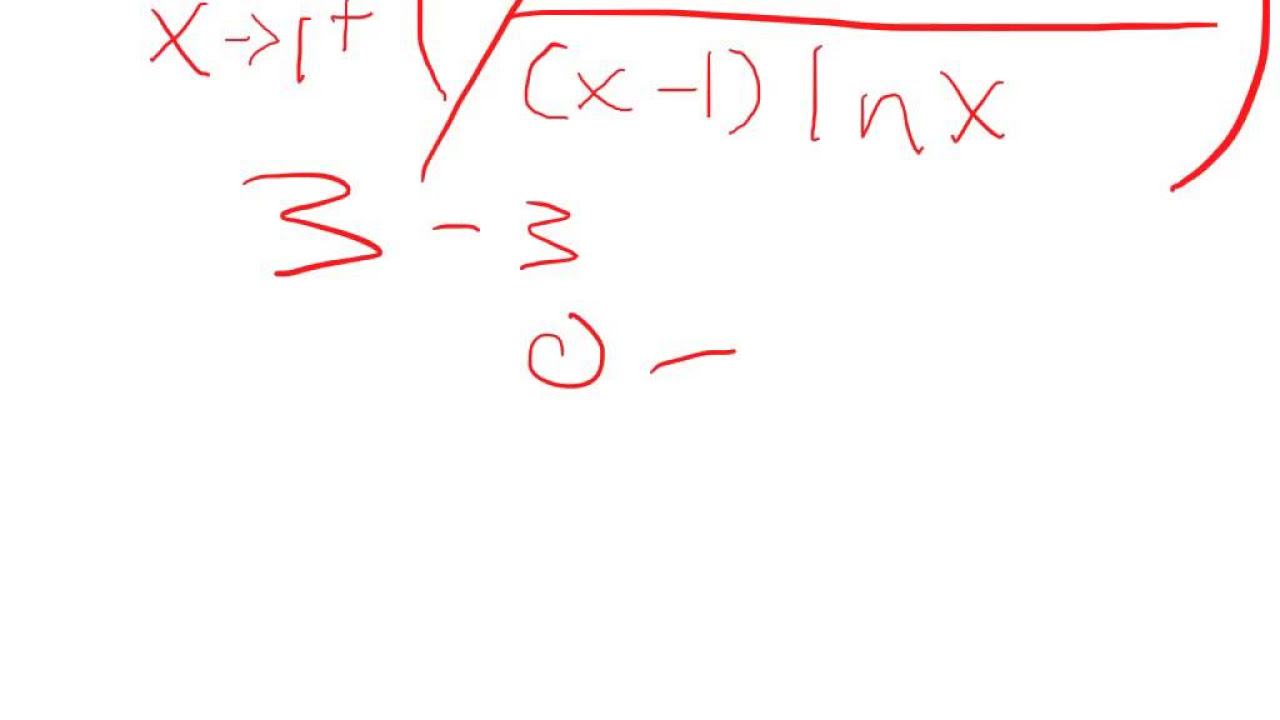Limits at Infinity With Radicals & Fractional Exponents

The Organic Chemistry Tutor
24 Jan 202006:14
EducationalLearning
32 Likes 10 Comments

TLDRThe video script presents a step-by-step solution to the mathematical problem of finding the limit of the x-root of x as x approaches infinity. The process involves converting the radical to a fractional exponent, applying logarithms to simplify the expression, and using L'Hopital's rule to evaluate the indeterminate form. The result is confirmed through a table of values showing that as x increases, the expression approaches one. The explanation is clear, methodical, and engaging, effectively guiding viewers through the solution.

Takeaways
  • 📚 The problem involves finding the limit of the expression 'x root of x' as x approaches infinity.
  • 🔍 The first step is to set the expression equal to a variable, in this case, y.
  • 🌱 Transforming the radical to a fractional exponent is crucial for simplification.
  • 📈 Using logarithms helps to reduce the exponent when dealing with variable over variable expressions.
  • 🧮 The natural logarithm (ln) of a variable can be used to simplify expressions involving products and exponents.
  • 📊 Indeterminate forms like infinity/infinity can be resolved using L'Hopital's rule.
  • 📚 L'Hopital's rule involves taking the derivatives of the numerator and the denominator and re-evaluating the limit.
  • 🔧 Direct substitution may not always work, and L'Hopital's rule is an alternative when it fails.
  • 📈 The limit of 1/x as x approaches infinity is zero, which is a key step in solving the problem.
  • 📝 The final answer is that the limit of the expression is 1, which can be confirmed by using a table of values.
  • 🔄 As x increases, the value of the expression 'x root of x' approaches 1, confirming the solution.
Q & A

  • What is the problem given in the transcript?

    -The problem given in the transcript is to find the limit, as x goes to infinity, of the expression x root of x.

  • How does the script suggest to start solving the problem?

    -The script suggests starting by setting the original expression equal to y, which helps in visualizing the limit as x approaches infinity.

  • What is the significance of converting the radical to a fractional exponent?

    -Converting the radical to a fractional exponent simplifies the expression and makes it easier to work with, allowing for further manipulation and application of logarithms to solve the limit problem.

  • Why is the natural log used in this problem?

    -The natural log is used because it helps to reduce the exponent when dealing with a variable raised to another variable, making it possible to solve the limit using logarithmic properties.

  • What property of logarithms is used to simplify the expression ln(x^(1/x))?

    -The property used is that ln(x^y) is equal to y * ln(x), which allows moving the exponent to the front and simplifying the expression further.

  • Why can't direct substitution be used immediately with the natural log of the limit?

    -Direct substitution can't be used immediately because it results in an indeterminate form of infinity divided by infinity, which does not provide a clear answer.

  • How does L'Hôpital's rule help in solving this problem?

    -L'Hôpital's rule helps by allowing the calculation of the limit when direct substitution results in an indeterminate form. It involves taking the derivatives of the numerator and the denominator and reevaluating the limit.

  • What is the result of applying L'Hôpital's rule to the limit problem?

    -Applying L'Hôpital's rule shows that the limit as x goes to infinity of the expression is equal to zero divided by one, which simplifies to zero.

  • How can the result of the limit problem be converted into an exponential expression?

    -The result can be converted into an exponential expression by using the relationship that if ln(y) = c, then e^c = y. Since the limit is zero, e^0 = 1, so the final answer is y = 1.

  • How does the script confirm the answer with a table of values?

    -The script confirms the answer by showing how the expression x root of x approaches 1 as x increases, with examples like 10^(1/10), 100^(1/100), and so on, all getting closer to 1 as x becomes larger.

  • What is the conclusion of the problem as presented in the transcript?

    -The conclusion is that the limit, as x goes to infinity, of the x root of x is equal to 1, which is confirmed through both the mathematical solution and the table of values.

Outlines
00:00
📚 Solving Limits with Logarithms

This paragraph introduces a mathematical problem concerning limits, specifically the limit of x as it approaches infinity in the expression x^(x). The speaker suggests setting the expression equal to y and transforming the radical into a fractional exponent. By applying the natural logarithm (ln) to both sides, the problem is simplified to finding the limit of ln(y) as x approaches infinity. The use of logarithmic properties and the application of L'Hôpital's rule to the indeterminate form leads to the conclusion that ln(y) equals zero, thus y equals e^0, which is 1. The solution is confirmed by examining values of the expression for increasing values of x, demonstrating that the expression approaches 1 as x becomes very large.

05:04
📈 Confirming the Limit with Numerical Examples

The second paragraph continues the discussion on the limit of the expression x^(x) as x approaches infinity by providing numerical examples. The speaker calculates the value of the expression for x as 10, 100, 1,000, and 10,000, showing that as x increases, the result converges towards 1. This numerical evidence supports the previously derived conclusion that the limit of the expression is indeed 1, reinforcing the understanding of the mathematical concept and its practical implications.

Mindmap
Keywords
💡Limit
In calculus, a limit is the value that a function (or sequence) approaches as the input (or index) approaches some value. In the video, the limit is discussed in the context of x approaching infinity for the expression x^(1/x). The concept of a limit is central as it helps to understand the behavior of functions at boundary points or infinity, leading to the conclusion that the expression tends towards 1.
💡Infinity
Infinity refers to something without any bound or end, often represented symbolically with the symbol ∞. In the transcript, infinity is used to describe the limit as x grows larger and larger, specifically considering the behavior of the function x^(1/x) as x approaches infinity. This helps to analyze the asymptotic behavior of the function.
💡Exponent
An exponent is a number or expression that indicates the power to which a base number is raised. In the script, the term 'x root of x' is transformed into x^(1/x), where (1/x) acts as the exponent, denoting the root of x. This transformation is crucial for further mathematical manipulation and understanding the nature of the function as x increases.
💡Natural log (ln)
The natural logarithm (ln) is the logarithm to the base e, where e is an irrational constant approximately equal to 2.71828. In the video, natural logarithms are used to simplify the expression x^(1/x) into a more manageable form for limit calculation, showing a common technique of bringing down exponents to facilitate differentiation.
💡L'Hôpital's rule
L'Hôpital's rule is a method in calculus for finding limits of indeterminate forms like 0/0 or ∞/∞. The transcript mentions this rule to resolve the indeterminate form encountered after transforming x^(1/x) and shows that after applying it, the limit simplifies to the derivative calculation, leading to a concrete value.
💡Derivative
A derivative represents the rate of change of a function with respect to a variable. In the context of the video, derivatives are used during the application of L'Hôpital's rule, specifically finding the derivative of ln(x) and x, which are 1/x and 1, respectively. This helps in determining the limit of the expression as x approaches infinity.
💡Exponential expression
An exponential expression is a mathematical expression in the form a^b, where a is the base and b is the exponent. The script transitions from a logarithmic form to an exponential expression, using e^0 = y to deduce that y equals 1, thus concluding the limit evaluation process.
💡Indeterminate form
Indeterminate forms are expressions in mathematical limit theory that do not have a definite limit or value without further analysis. The video script addresses the indeterminate form ∞/∞ when discussing the limit of ln(x)/x, which necessitates the use of L'Hôpital's rule to find a determinate value.
💡Substitution
Substitution in mathematics is the replacement of a variable or an expression with another. In the video, substitution is initially used to evaluate the limit directly, which leads to an indeterminate form, and then to apply L'Hôpital's rule effectively, simplifying the expression to find the limit.
💡Convergence
Convergence refers to the property of a sequence or function approaching a specific value as the variable or index increases. The video illustrates convergence through numerical examples, showing that as x increases, x^(1/x) gets closer to 1, validating the calculated limit.
Highlights

The problem involves finding the limit of a function as x approaches infinity.

The original expression is set equal to y to simplify the problem.

The radical (root) expression is transformed into a fractional exponent for easier manipulation.

The use of natural logarithms is suggested to simplify the variable raised to a variable expression.

Properties of logarithms are used to simplify the expression further.

An indeterminate form of infinity divided by infinity is encountered.

L'Hôpital's rule is applied to evaluate the limit when direct substitution fails.

Derivatives of the numerator and denominator are taken to apply L'Hôpital's rule.

Direct substitution is used again after simplifying the expression with L'Hôpital's rule.

The limit is found to be zero, which leads to the conclusion that ln y equals zero.

The relationship between logarithms and exponential expressions is used to solve for y.

The final answer is that y equals one, as x approaches infinity.

The answer is confirmed with a table of values showing the trend as x increases.

The table demonstrates that the expression approaches one as x becomes larger.

The problem-solving process exemplifies the application of advanced mathematical techniques.

The method can be applied to similar problems involving limits and indeterminate forms.

Transcripts

Browse More Related Video

Limits at infinity of quotients with square roots (even power) | AP Calculus AB | Khan Academy

A Limit Example Combining Multiple Algebraic Tricks

finally 0^0 approaches 0 after 6 years!

Ryan and Nick do L'hopital's rule

my all-in-one calculus question

Limits of Logarithmic Functions | Calculus

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusLimitsLogarithmsL'Hopital's RuleInfinite SeriesMathematicsEducationProblem SolvingAdvanced Math极限求解