Computing Limits at Infinity for Rational Functions
TLDRThe video script presents a standard methodology for computing limits at infinity for rational functions, specifically polynomials divided by polynomials. The speaker illustrates the process using three examples, each with different highest powers in the numerator and denominator. The key insight is to focus on the terms with the highest power, as they dominate the behavior of the function as X approaches infinity. The script details a rigorous approach by multiplying the numerator and denominator by the reciprocal of the highest power term, simplifying the expression and allowing the application of limit laws. This method systematically leads to the conclusion that if the highest power in the numerator is greater than in the denominator, the function diverges to infinity; if they are equal, it tends to a constant fraction; and if the denominator's power is higher, the function approaches zero. The summary emphasizes the importance of logical steps and proper theorems in mathematical reasoning.
Takeaways
- 📚 When computing limits at infinity for rational functions, focus on the highest power of the polynomials in the numerator and denominator.
- 🔍 For large values of x, the highest power terms dominate the behavior of the function, making lower power terms negligible.
- 💡 Multiplying the numerator and denominator by the reciprocal of the highest power term (e.g., 1/x^n) simplifies the function for limit evaluation.
- 🚀 If the highest power in the numerator is greater than in the denominator, the function approaches infinity as x grows large.
- 📉 Conversely, if the highest power in the denominator is greater, the function approaches zero as x increases.
- 🔄 When the highest powers are equal, the limit is determined by the next lower power terms, resulting in a constant fraction.
- 🧮 Use limit laws to handle sums and quotients of terms that approach zero, as their individual limits can be summed or divided.
- 🤔 Always verify naive guesses with rigorous mathematical proofs to ensure accuracy.
- 📐 The process of dividing by the highest power term allows for the cancellation of x terms, leaving behind the coefficients which determine the limit.
- 🌐 As x approaches infinity, terms involving 1/x, 1/x^2, or 1/x^3 will approach zero, simplifying the function for limit evaluation.
- 📉 In cases where the denominator's highest power exceeds the numerator's, the limit of the function is zero.
- 📈 When the numerator's highest power is greater, the function diverges to infinity, indicating that there is no limit as x approaches infinity.
Q & A
What is the primary method discussed in the video for computing limits at infinity for rational functions?
-The primary method discussed is to look at the highest power of the polynomials in the numerator and the denominator. If the powers are the same, the limit tends to a constant fraction. If the numerator has a higher power, the limit tends to infinity, and if the denominator has a higher power, the limit tends to zero.
How does the video suggest simplifying the process of finding limits at infinity for rational functions?
-The video suggests simplifying by multiplying both the numerator and the denominator by the reciprocal of the highest power of x present in the denominator, which allows us to focus on the coefficients of the highest powers.
What happens to the limit of a rational function as x approaches infinity if the degree of the polynomial in the numerator is higher than the denominator?
-If the degree of the polynomial in the numerator is higher than the denominator, the limit of the rational function as x approaches infinity will diverge to infinity.
What is the result of the limit as x approaches infinity for a rational function where the degree of the polynomial in the numerator is less than the denominator?
-If the degree of the polynomial in the numerator is less than the denominator, the limit of the rational function as x approaches infinity will approach zero.
How does the video justify the approximation of the limit to 1/3 for the first example given?
-The video justifies this by multiplying both the numerator and the denominator by 1/x^3, which simplifies the expression to terms with 1/x, 1/x^2, and 1/x^3 in the numerator and a 3x in the denominator. As x approaches infinity, the terms with 1/x powers go to zero, leaving only the 1/3 from the 3x in the denominator.
What does the video imply about the limit of a rational function when the highest power of x in both the numerator and the denominator is the same?
-When the highest power of x in both the numerator and the denominator is the same, the limit of the rational function as x approaches infinity will be a constant fraction, which is the ratio of the coefficients of the highest powers.
Why does the video emphasize the importance of not just guessing the answer and instead using proper theorems?
-The video emphasizes this to ensure mathematical rigor and to avoid logical errors. It's important to verify guesses with established theorems and to follow a formal process to ensure the correctness of the solution.
What is the role of the limit laws in the process of computing limits at infinity for rational functions?
-The limit laws are used to handle the sum or quotient of terms that individually approach zero. They allow us to break down the expression into simpler parts, take the limit of each part, and then combine the results to find the overall limit.
How does the video script illustrate the concept of limits at infinity with the second example provided?
-The second example changes the highest power in the numerator to x^4 and in the denominator to x^3. The video shows that the limit as x approaches infinity will diverge to infinity because the highest power in the numerator dominates.
What is the final conclusion the video script draws about the behavior of limits at infinity for rational functions?
-The final conclusion is that for rational functions, the behavior of the limit at infinity can be determined by examining the highest powers of x in the numerator and the denominator. If the top power is greater, the limit is infinity; if the bottom power is greater, the limit is zero; and if they are equal, the limit is a constant fraction.
What is the significance of the 'naive computation' mentioned in the video?
-The 'naive computation' is a quick estimation method used to guess the limit at infinity before applying the rigorous mathematical process. It provides an initial intuition which is then verified through a formal mathematical approach for accuracy and correctness.
How does the video script handle the concept of limits at infinity for rational functions with changing highest powers in the numerator and denominator?
-The script provides a step-by-step method to handle different scenarios by changing the highest powers in the examples. It shows how to adjust the process for each case, whether the highest power is in the numerator, the denominator, or they are equal.
Outlines
📚 Understanding Limits at Infinity for Rational Functions
This paragraph introduces the concept of computing limits at infinity for rational functions, specifically when dealing with polynomials divided by polynomials. The speaker uses an example to illustrate the process, emphasizing the importance of focusing on the highest power of x in both the numerator and the denominator. They explain that as x becomes very large, the size of the function is primarily determined by the largest power of x in the numerator and denominator. The speaker then demonstrates a method to rigorously determine the limit by multiplying both the numerator and denominator by the reciprocal of the highest power of x, simplifying the expression and allowing for easier computation of the limit. The process is shown to yield a limit of 1/3 for the given example, verifying the initial guess through mathematical proof.
🔍 Analyzing Divergent and Convergent Limits of Rational Functions
The second paragraph delves into further examples to explore when rational functions diverge to infinity or converge to a finite limit as x approaches infinity. The speaker discusses how the highest power of x in the numerator and denominator dictates the behavior of the limit. If the highest power in the numerator is greater than in the denominator, the function diverges to infinity. Conversely, if the highest power is in the denominator, the function converges to zero. The speaker reinforces the method of dividing both the numerator and denominator by the highest power of x to simplify the expression and more clearly identify the nature of the limit. Examples are provided to show how this approach can be applied to different rational functions, leading to the conclusion that the limit is either a fraction, infinity, or zero, depending on the relative powers of x in the numerator and denominator.
Mindmap
Keywords
💡Rational Function
💡Polynomial
💡Limit at Infinity
💡Divide by the Highest Power
💡Numerator
💡Denominator
💡Limit Laws
💡Divergence
💡Convergence
💡Factoring
💡1/x
Highlights
The video introduces a standard methodology for computing limits at infinity of rational functions, specifically a polynomial divided by a polynomial.
The presenter uses an example to illustrate the concept, focusing on the behavior of the function as the variable X becomes very large.
It is explained that when X is extremely large, the constant terms in the polynomials become negligible, and the highest power of X determines the behavior of the function.
The presenter suggests a naive computation method by focusing on the highest power terms and canceling them out to simplify the expression.
To ensure accuracy, the presenter emphasizes the importance of using proper theorems and avoiding logical errors in mathematical reasoning.
A rigorous approach is demonstrated by multiplying the numerator and denominator by the reciprocal of the highest power of X to simplify the expression.
The limit laws for infinity are applied to show that terms with X in the denominator approach zero as X goes to infinity.
The presenter verifies the initial guess by showing that the simplified expression results in a value of one-third.
A second example is provided to illustrate a case where the function diverges to infinity as X approaches infinity.
The presenter emphasizes the importance of considering the highest power terms in the numerator and denominator to predict the behavior of the function at infinity.
The process of dividing both the numerator and denominator by the highest power of X is shown to simplify the expression for limit calculations.
The presenter demonstrates that if the highest power in the numerator is greater than the denominator, the function diverges to infinity.
Conversely, if the highest power is in the denominator, the function approaches zero as X goes to infinity.
The video concludes with a final example where the highest power in the numerator is less than the denominator, resulting in a limit of zero.
The presenter summarizes the process of computing limits at infinity for rational functions by comparing the highest powers of X in the numerator and denominator.
The importance of a formal approach over naive guessing is stressed for mathematical rigor and accuracy.
The video provides a clear and methodical explanation of limit calculations at infinity for rational functions, making it accessible for learners.
Transcripts
Browse More Related Video
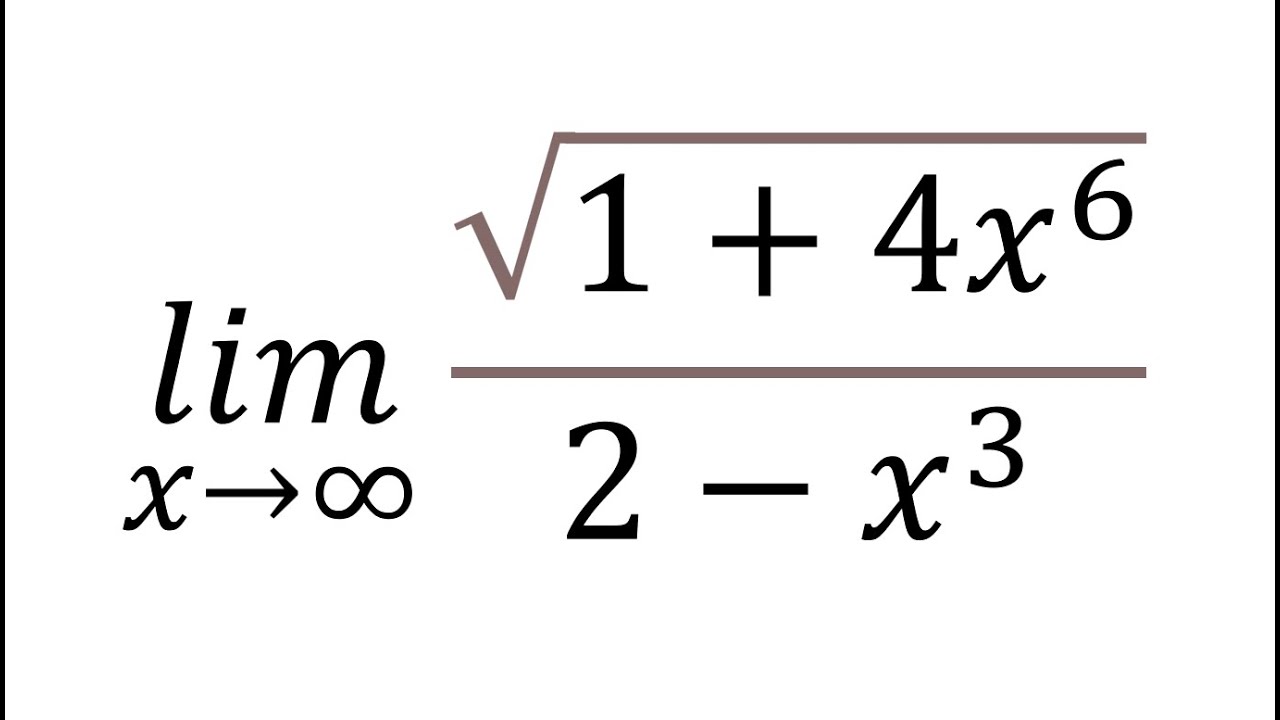
Find limit at Infinity | sqrt(1+4x^6)/(2-x^3) x approaches infinity | general solution

Calculus:Limits of Rational Functions

Limits at infinity of quotients (Part 2) | Limits and continuity | AP Calculus AB | Khan Academy

Limits at infinity of quotients with square roots (even power) | AP Calculus AB | Khan Academy

Business Calculus - Math 1329 - Section 1.5 (and 1.6) - Limits and Continuity

Limits at infinity of quotients (Part 1) | Limits and continuity | AP Calculus AB | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: