Find limit at Infinity | sqrt(1+4x^6)/(2-x^3) x approaches infinity | general solution
TLDRThis video script explains the method to calculate the limit of a fraction as x approaches infinity, where both numerator and denominator are polynomials. It emphasizes comparing the highest degree of both parts, as the highest power term dominates when x is very large. The script outlines three scenarios: if the numerator's degree is less than the denominator's, the limit approaches zero; if they are equal, the limit is the ratio of coefficients; and if the numerator's degree is higher, the limit is infinity. Special attention is given to the sign when considering negative infinity. The example provided involves a square root, requiring the square root to be opened first before applying the rules.
Takeaways
- 🔍 To find the limit of a function as x approaches infinity, compare the highest degree of the numerator and the denominator of the polynomials involved.
- 📚 The highest degree terms are the most significant when x approaches infinity, as they grow faster than lower degree terms.
- 👉 If the degree of the numerator is less than the denominator, the limit approaches zero.
- 🔄 When the degrees of the numerator and denominator are the same, the limit is determined by the ratio of the coefficients of the highest degree terms.
- ⏫ If the numerator's degree is greater than the denominator's, the limit approaches infinity, with attention to the sign of the limit if x approaches negative infinity.
- 🌐 Opening up square roots can be necessary to simplify the expression before comparing degrees.
- 📉 For limits where the numerator's degree is less, a constant divided by an increasingly large number (x) results in zero.
- 📈 When the degrees match, the coefficients of the highest degree terms (after simplification) give the limit.
- 🔢 In cases of equal degrees, dividing the highest degree term from both the numerator and the denominator simplifies to the coefficient ratio.
- 📌 Pay attention to the sign of the terms when calculating limits, as it can affect whether the limit is positive or negative infinity.
- 📝 The script provides a methodical approach to solving limit problems involving polynomials and roots, emphasizing the importance of the highest degree terms.
Q & A
What is the main focus of the video script regarding limits?
-The video script focuses on calculating the limit of a fraction where both the numerator and the denominator are polynomials, and sometimes includes a square root sign. It emphasizes the importance of comparing the highest degree of the numerator and the denominator to determine the limit as x approaches infinity.
Why is it important to look at the highest degree term when calculating limits of polynomials?
-The highest degree term is important because as x approaches infinity, this term grows the fastest and outgrows all other terms. Therefore, it is the most significant in determining the limit.
What happens to the limit when the degree of the numerator is less than the degree of the denominator?
-When the degree of the numerator is less than the degree of the denominator, the limit approaches zero because a constant divided by an increasingly large number approaches zero.
How does the limit change if the degree of the numerator is the same as the degree of the denominator?
-If the degrees are the same, the limit is determined by the ratio of the coefficients of the highest degree terms. The limit simplifies to the coefficient of the highest degree term in the numerator divided by that in the denominator.
What is the result of the limit when the degree of the numerator is greater than the degree of the denominator?
-When the degree of the numerator is greater than the degree of the denominator, the limit approaches infinity, as the highest degree term in the numerator grows without bound faster than the denominator.
What should be considered when dealing with limits as x approaches negative infinity?
-When x approaches negative infinity, one must pay attention to the sign of the terms, especially if the highest degree term is a simple x, as this could lead to the limit approaching negative infinity.
How does the presence of a square root sign affect the calculation of the limit?
-The presence of a square root sign requires that you first open up the square root, effectively doubling the exponent of the term under the root, before comparing the degrees of the numerator and the denominator.
Can the method described in the script be applied to all types of limits?
-The method is primarily applicable to limits involving polynomials and can be adapted for cases with square roots. However, it may not be directly applicable to non-polynomial functions or more complex expressions.
What is the significance of the coefficient in determining the limit when the degrees of the numerator and denominator are the same?
-The coefficient is significant because it dictates the rate at which the terms grow as x approaches infinity. The limit is the ratio of the coefficients when the degrees are equal.
How can you simplify the limit calculation when the degrees of the numerator and denominator are the same?
-You can simplify the calculation by dividing both the numerator and the denominator by the highest degree term, which usually is x raised to the power of the degree, leaving you with the ratio of the coefficients.
What is the final step in the script's example for calculating the limit of a fraction with a square root in the numerator?
-The final step is to open up the square root in the numerator, compare the degrees of the resulting terms with the denominator, and then simplify the expression to find the limit, which in the example is the ratio of the coefficients of the highest degree terms.
Outlines
📚 Understanding Limits of Polynomials
This paragraph introduces the concept of calculating limits as x approaches infinity for fractions where both the numerator and the denominator are polynomials. It emphasizes the importance of comparing the highest degrees of the polynomials to determine the limit. The speaker explains that the highest power term will dominate as x grows large, allowing lower degree terms to be ignored. The paragraph outlines three scenarios: when the numerator's degree is less than the denominator's, resulting in a limit of zero; when they are equal, leading to a limit equal to the ratio of the coefficients; and when the numerator's degree is greater, which is not fully explained here but implies the limit would be infinity.
🔍 Calculating Limits with Roots and Signs
The second paragraph delves into the specifics of calculating limits when there are roots involved and emphasizes the need to pay attention to the sign of the limit, especially when x approaches negative infinity. The speaker provides an example of opening up a square root in the numerator and focusing on the highest degree term, which in this case is 2x^3, to simplify the limit calculation. The paragraph concludes by reiterating the method of dividing the highest degree term on both the numerator and the denominator to find the limit when the degrees are equal, and also suggests a more mathematical approach for a strict proof.
Mindmap
Keywords
💡Limit
💡Polynomials
💡Numerator
💡Denominator
💡Highest Degree
💡Infinity
💡Coefficient
💡Square Root
💡Growth Rate
💡Simplification
💡Contextualization
Highlights
The importance of comparing the highest degree of the numerator and denominator when calculating limits as x approaches infinity.
Focusing on the term with the highest power in polynomials when x approaches infinity, as it grows the fastest and outgrows other terms.
Three categories for limits based on the degree comparison: numerator less than, equal to, or greater than the denominator.
If the numerator degree is less than the denominator, the limit approaches zero.
For equal degrees, the limit is determined by the ratio of the coefficients of the highest degree terms.
When the numerator degree is higher, the limit approaches infinity, with attention to the sign for negative infinity.
The method of simplifying the fraction by dividing the highest degree terms by x when degrees are equal.
The significance of the sign in determining the direction of infinity when x approaches negative infinity.
How to deal with square root signs in limits by opening them up to compare degrees correctly.
Ignoring terms of lower degrees when calculating limits as they are less significant.
The concept of the highest power term dominating the behavior of the limit as x approaches infinity.
A step-by-step explanation of how to calculate limits with polynomials and square roots.
The mathematical trick of focusing on the highest degree term for determining the limit of a fraction as x approaches infinity.
An example of calculating the limit with a polynomial numerator and a cubic term in the denominator.
The result of the limit calculation when the degree of the numerator is the same as the denominator.
A strict mathematical proof approach by dividing x to the third on both the top and bottom of the fraction.
The final result of the limit calculation for the given example in the transcript.
Transcripts
Browse More Related Video

Limits at infinity of quotients with square roots (even power) | AP Calculus AB | Khan Academy

Computing Limits at Infinity for Rational Functions

Limits at infinity of quotients (Part 1) | Limits and continuity | AP Calculus AB | Khan Academy

Limits at infinity of quotients (Part 2) | Limits and continuity | AP Calculus AB | Khan Academy
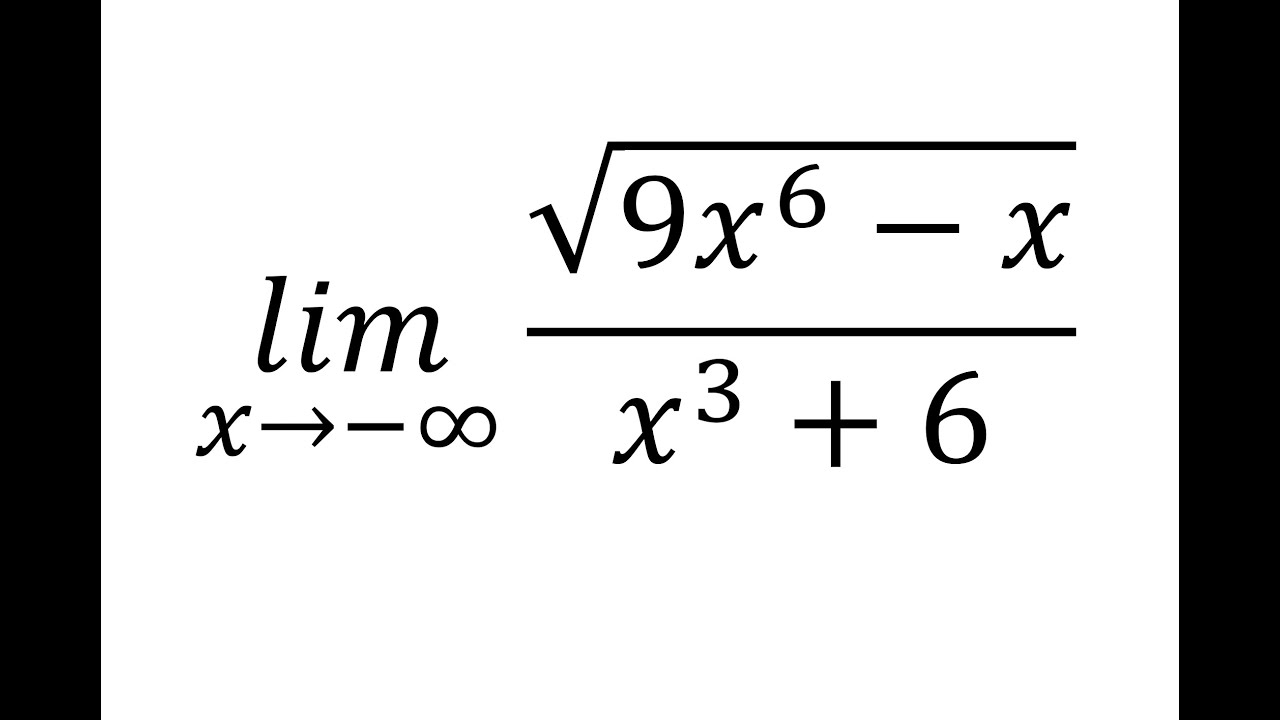
Limits at Infinity (Rational square-root function as x approaches negative Infinity)

Finding a Horizontal Asymptote of a Rational Function (Precalculus - College Algebra 40)
5.0 / 5 (0 votes)
Thanks for rating: