Green's theorem example 2 | Multivariable Calculus | Khan Academy
TLDRThe video script discusses the application of Green's theorem to calculate the line integral of a function over a unit circle traversed in a clockwise direction. It highlights the importance of orientation in Green's theorem, explaining that the theorem yields a negative result when the integration is counterclockwise, but the region of interest is to the right of the curve. The script simplifies the problem by recognizing that the integral over the unit circle is equivalent to the area of the circle, which is pi. The final result of the line integral is thus 5 pi, demonstrating the efficiency of using Green's theorem over more complex methods.
Takeaways
- 📐 The problem involves a line integral around a unit circle in the xy-plane, traversed clockwise.
- 🔄 The unit circle is defined by the equation x^2 + y^2 = 1, with a radius of 1 unit.
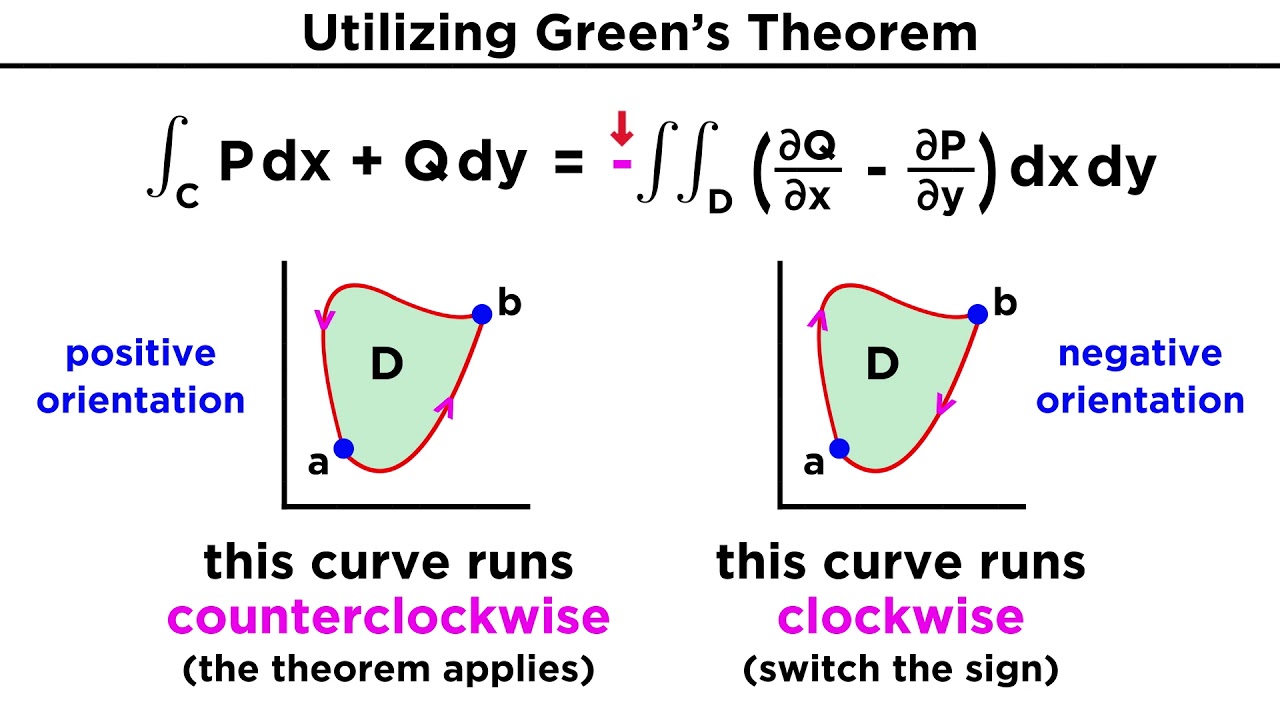
- 🔄 The direction of traversal affects the application of Green's theorem; counterclockwise traversal is the standard for Green's theorem.
- 📈 The given line integral is ∫(2y dx - 3x dy) over the closed curve c.
- 🎓 Green's theorem relates the line integral of a vector field around a closed curve to a double integral over the enclosed region.
- 🤔 The region to the right of the traversed curve requires a modification when applying Green's theorem, resulting in a negative sign.
- 📚 The partial derivatives of P and Q are calculated: ∂P/∂y = 2 and ∂Q/∂x = -3.
- 🧩 The double integral simplifies to an integral over the region R of (∂Q/∂x - ∂P/∂y) dxdy, which represents the area of the enclosed region.
- 🌐 The area of the unit circle is calculated using the formula πr^2, where r = 1, resulting in an area of π.
- 🔢 The final result of the line integral is 5π, achieved by applying Green's theorem and considering the direction of traversal.
- 💡 The example demonstrates the efficiency of Green's theorem in solving line integrals compared to other methods, such as setting up a double integral from scratch.
Q & A
What is the path described in the xy plane?
-The path described is the unit circle in the xy plane, traversed in a clockwise direction.
What is the equation of the unit circle?
-The equation of the unit circle is x squared plus y squared equals 1, representing a circle with a radius of 1 unit.
What is the line integral being calculated over curve c?
-The line integral being calculated is of the form ∫(2y dx - 3x dy) over the closed curve c, which is the unit circle traversed clockwise.
Why can't Green's theorem be directly applied to this problem?
-Green's theorem typically applies when the curve is traversed counterclockwise and the region is to the left of the curve. Since the unit circle is traversed clockwise and the region is to the right, the application of Green's theorem will yield a negative result.
How does the direction of traversal affect the application of Green's theorem?
-The direction of traversal affects the sign of the result when applying Green's theorem. Clockwise traversal results in a negative value, while counterclockwise traversal gives a positive value.
What are P(x, y) and Q(x, y) in the context of Green's theorem?
-In the context of Green's theorem, P(x, y) is the function represented by 2y, and Q(x, y) is the function represented by -3x.
What are the partial derivatives calculated in the example?
-The partial derivative of P with respect to y (∂P/∂y) is 2, and the partial derivative of Q with respect to x (∂Q/∂x) is -3.
How is the double integral over the region represented in the final calculation?
-The double integral over the region is represented as the integral over the area of the unit circle, which is pi times the radius squared (pi * 1^2), simplifying to just pi.
What is the final result of the line integral calculation?
-The final result of the line integral calculation is 5 times pi (5π), obtained by applying Green's theorem correctly with consideration of the direction of traversal.
What is the significance of the area of the unit circle in this problem?
-The area of the unit circle, which is pi, is significant because it represents the region over which the double integral is calculated in the application of Green's theorem.
How does the use of Green's theorem simplify the calculation compared to other methods?
-Using Green's theorem simplifies the calculation by allowing us to convert the line integral into a double integral over the area enclosed by the curve, which in this case, is the area of the unit circle. This is less complex than setting up a double integral directly using antiderivative methods.
Outlines
📐 Understanding the Unit Circle and Line Integral
This paragraph introduces the concept of a unit circle in the xy plane and the process of traversing it in a clockwise direction. It explains the equation of the unit circle (x squared plus y squared equals 1) and sets the stage for discussing the line integral over a closed curve c. The paragraph delves into the application of Green's theorem for calculating the line integral, highlighting the importance of the direction of traversal (clockwise in this case) and how it affects the sign of the result. The explanation includes the formula for Green's theorem and the steps to apply it to the given problem, emphasizing the need to adjust the formula based on the orientation of the curve and the region.
🧠 Simplifying the Problem Using Green's Theorem
The second paragraph focuses on simplifying the line integral problem using Green's theorem. It explains how the double integral over the region R represents the area of the unit circle, which is calculated using the formula pi times the radius squared. The paragraph clarifies that the area of the unit circle is pi, given that the radius is 1. It then shows how the line integral can be expressed as 5 times the area of the unit circle, resulting in the final answer of 5 pi. The speaker also challenges the listener to solve the problem without using Green's theorem, suggesting that it would be more complex and less straightforward than the method demonstrated.
Mindmap
Keywords
💡xy plane
💡unit circle
💡line integral
💡Green's theorem
💡counterclockwise
💡partial derivatives
💡double integral
💡area
💡parameterization
💡antiderivative
Highlights
The discussion revolves around a line integral over a unit circle in the xy plane, which is a fundamental concept in calculus.
The unit circle is traversed in a clockwise direction, which is important when applying Green's theorem.
The equation of the unit circle is x squared plus y squared equals 1, representing a circle with a radius of 1 unit.
The vector field for the line integral is given as 2y dx minus 3x dy, which is key to the calculation.
Green's theorem is applicable for calculating line integrals over closed curves, and it relates the line integral to a double integral over the enclosed region.
A crucial point is that Green's theorem typically applies when the curve is traversed counterclockwise, which affects the sign of the result.
The region of interest is to the right of the traversed curve when moving clockwise, which impacts the application of Green's theorem.
The line integral can be simplified by applying Green's theorem, which results in a double integral over the enclosed region.
The partial derivatives of P and Q with respect to y and x respectively are calculated, resulting in 2 and -3.
The double integral simplifies to the integral over the region of 5 dA, where 5 is a constant.
The area of the unit circle, which is the region of interest, is calculated as pi r squared, where r is the radius.
The final answer to the line integral is 5 pi, derived from the area of the unit circle and the constant factor from the double integral.
The method of solving the line integral using Green's theorem is highlighted as simpler compared to other methods.
The importance of the direction of traversal (clockwise or counterclockwise) is emphasized for the correct application of Green's theorem.
The practical application of Green's theorem in calculating line integrals over specific curves in the xy plane is demonstrated.
The transcript provides a clear and detailed explanation of the mathematical concepts involved, making it accessible for learning.
The process of calculating the line integral using Green's theorem is outlined step by step, offering a comprehensive guide.
The example serves as a practical illustration of the theoretical concepts of line integrals and Green's theorem in a real-world context.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: