Green's Theorem, explained visually
TLDRThis video explores the connection between double integrals and line integrals through Green's theorem. It explains how the line integral of a 2D vector field over a closed curve is equivalent to the double integral of the field's curl over the enclosed region. The video also discusses the concept of curl, which measures rotation in a vector field, and demonstrates how to calculate the line integral using the curl in a step-by-step manner.
Takeaways
- 📚 The video discusses the relationship between a double integral and a line integral using Green's theorem.
- 🌀 Green's theorem states that the line integral of a 2-dimensional vector field \( \vec{F} \) over a closed curve \( C \) is equal to the double integral of the curl of \( \vec{F} \) over the region \( R \) inside the curve.
- 📉 The curl of a vector field in two dimensions measures the rotation within the field, with positive curl indicating counterclockwise rotation and negative indicating clockwise.
- 🔍 The curl can be represented as a cross product between the del vector (a vector containing all partial derivatives) and the vector field.
- 🔄 The rotation of a region \( R \) affects the sign of the line integral: counterclockwise gives a positive value, clockwise gives a negative one.
- 🛤️ The script explains that a curve can be split into multiple curves, and the line integrals can be summed to equal the line integral over the original curve.
- 🧩 By dividing the region into many small parts, the line integral can be approximated by summing the product of curl and the area of each small region, which is essentially a double integral.
- 📐 The script uses the idea of infinite approximations, similar to Riemann sums in calculus, to transition from summing areas to the integral.
- 🔗 The double integral, which relates to the region inside the curve, can be described by looking at the edges, similar to the fundamental theorem of calculus.
- 📘 An example is given where the line integral of a vector field \( \vec{F} \) over a curve \( C \) is calculated by evaluating the double integral of the 2-dimensional curl over the region \( R \).
- 🚀 The video concludes with a teaser for future content on three-dimensional analogs of these concepts, such as Stokes' theorem and the divergence theorem.
Q & A
What is the main topic of the video?
-The main topic of the video is to establish a relationship between a double integral and a line integral using Green's theorem in the context of a 2-dimensional vector field.
What is a vector field?
-A vector field is a mathematical concept where every point in space is assigned a vector, indicating direction and magnitude at that point.
What is Green's theorem?
-Green's theorem is a result in vector calculus that relates the line integral of a vector field around a closed curve to the double integral of the curl of the vector field over the region enclosed by the curve.
What are the requirements for the curve C in the context of Green's theorem?
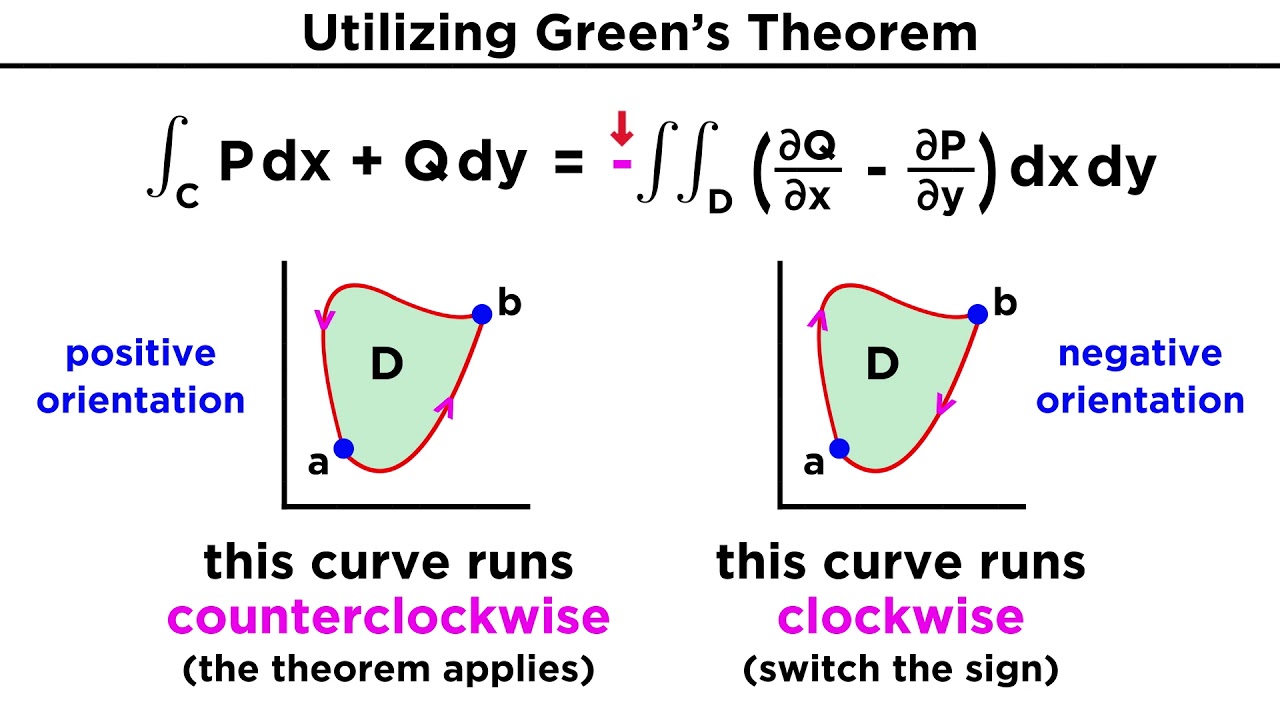
-The curve C must be closed and oriented counterclockwise for Green's theorem to apply.
What does the curl of a vector field in two dimensions represent?
-In two dimensions, the curl of a vector field represents a measure of rotation over a region in the vector field, indicating whether the rotation is clockwise or counterclockwise.
How does the sign of the curl indicate the direction of rotation?
-A positive curl indicates counterclockwise rotation, while a negative curl indicates clockwise rotation.
What is the significance of splitting the line integral into two curves?
-Splitting the line integral into two curves allows us to understand that the resulting integral is the sum of the line integrals over each curve, which is equivalent to the line integral over the entire curve due to the cancellation of the center line.
How can the line integral of a vector field be approximated using the concept of curl?
-The line integral can be approximated by summing up the curl times a small region for every point in the region, which essentially forms a double integral.
What is the connection between the double integral and the line integral in the context of Green's theorem?
-According to Green's theorem, the line integral of a vector field over a closed curve is equal to the double integral of the curl of the vector field over the region enclosed by the curve.
How does the video script illustrate the approximation of the line integral using infinitesimally small rectangles?
-The script uses the concept of Riemann sums to show that as the size of the rectangles approaches zero, the curl of the vector field becomes a better approximation for the line integral of each small piece, leading to the summation of the curl over the entire region.
What is the analogy between the double integral related to the region inside the curve and the fundamental theorem of calculus?
-The analogy is that just as the fundamental theorem of calculus states that the area under a curve can be described by looking at the endpoints, the double integral of the region inside a curve can be described by looking at its edges.
What are the next topics the video series will cover?
-The next videos will cover three-dimensional applications of similar concepts, including Stokes theorem and the divergence theorem.
Outlines
📚 Introduction to Green's Theorem and Vector Fields
This paragraph introduces the concept of Green's Theorem, which is a fundamental theorem relating double integrals to line integrals. The video begins by explaining the prerequisites for understanding line integrals and vector fields, which are essential for grasping the theorem. A vector field assigns a vector to every point in space, and the video uses color to illustrate this concept. The line integral involves a closed curve, C, which must be oriented counterclockwise. The region inside this curve is denoted as R. Green's Theorem equates the line integral of a vector field F over curve C to the double integral of the two-dimensional curl of F over region R. The curl, represented as a cross product, indicates the rotation within the vector field, with positive curl indicating counterclockwise rotation and negative indicating clockwise. The paragraph also discusses how the line integral can be split into parts corresponding to different curves, leading to the idea that the line integral of the entire curve can be found by summing the integrals of its parts.
🔍 Applying Green's Theorem with an Example
In this paragraph, the script provides a practical example of applying Green's Theorem. It presents a vector field F and a curve C, and the task is to calculate the line integral of F over C. According to Green's Theorem, this line integral is equivalent to the double integral of the two-dimensional curl of the vector field over the region inside C. The example calculates the curl of the given vector field, which results in the expression x-9. To evaluate the line integral, the double integral of this expression over the region R is performed, with the region defined by the top line y=3-x and the bottom line y=-1, and the x-limits from -1 to 1. The calculation yields a result of -218/3. The paragraph concludes by mentioning upcoming videos that will explore three-dimensional applications of these concepts, such as Stokes' Theorem and the Divergence Theorem, and thanks the viewers for watching.
Mindmap
Keywords
💡Double Integral
💡Line Integral
💡Green's Theorem
💡Vector Field
💡Curl
💡Del Vector
💡Rotation
💡Riemann Sums
💡Approximation
💡Stokes' Theorem
💡Divergence Theorem
Highlights
Building a relation between a double integral and the line integral using Green's theorem.
Introduction to the concept of a 2-dimensional vector field and its representation.
Requirement for the curve C in a line integral: it must be closed and oriented counterclockwise.
Green's theorem equates the line integral of a vector field over a curve to the double integral of the curl over a region.
Curl in a 2D vector field indicates the sense of rotation and can be positive or negative.
Curl can be represented as a cross product between the Del vector and the vector field.
Significance of the overall rotation of region R in determining the sign of the line integral.
The ability to split a line integral into multiple curves and the implications for the integral's value.
Approximation of the line integral by summing the curl times a small region for each point in the vector field.
The concept of infinite approximations in calculus and its application to the double integral.
The equivalence of the line integral over a vector field to the double integral of its curl.
The analogy between the double integral related to a region inside a curve and the fundamental theorem of calculus.
Practical application of Green's theorem in calculating the line integral of a given vector field over a curve.
Calculation of the two-dimensional curl of a vector field as part of the process.
Evaluation of the double integral to find the value of the line integral.
Introduction to the upcoming topics of Stokes theorem and the divergence theorem in future videos.
Encouragement for viewers to stay tuned for further exploration of these topics.
Transcripts
Browse More Related Video

Stokes's Theorem
Green's Theorem

Green's theorem proof (part 2) | Multivariable Calculus | Khan Academy

Green's theorem proof part 1 | Multivariable Calculus | Khan Academy

Green's and Stokes' theorem relationship | Multivariable Calculus | Khan Academy

Stokes example part 4: Curl and final answer | Multivariable Calculus | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: