Green's theorem example 1 | Multivariable Calculus | Khan Academy

Khan Academy

7 Mar 201010:31

EducationalLearning

32 Likes 10 Comments

TLDRThe video script discusses the application of Green's theorem to solve line integrals, clarifying the directionality aspect of the path in relation to the region. It proceeds to illustrate a step-by-step solution of a specific line integral involving a curve defined by a region, calculating the integral of the given function over the boundary of the region. The solution is methodically derived, resulting in the final answer of 16/15, demonstrating the power of Green's theorem in simplifying complex integrals.

Takeaways

📜 Green's theorem is a method used to solve line integrals and can be applied to specific regions.
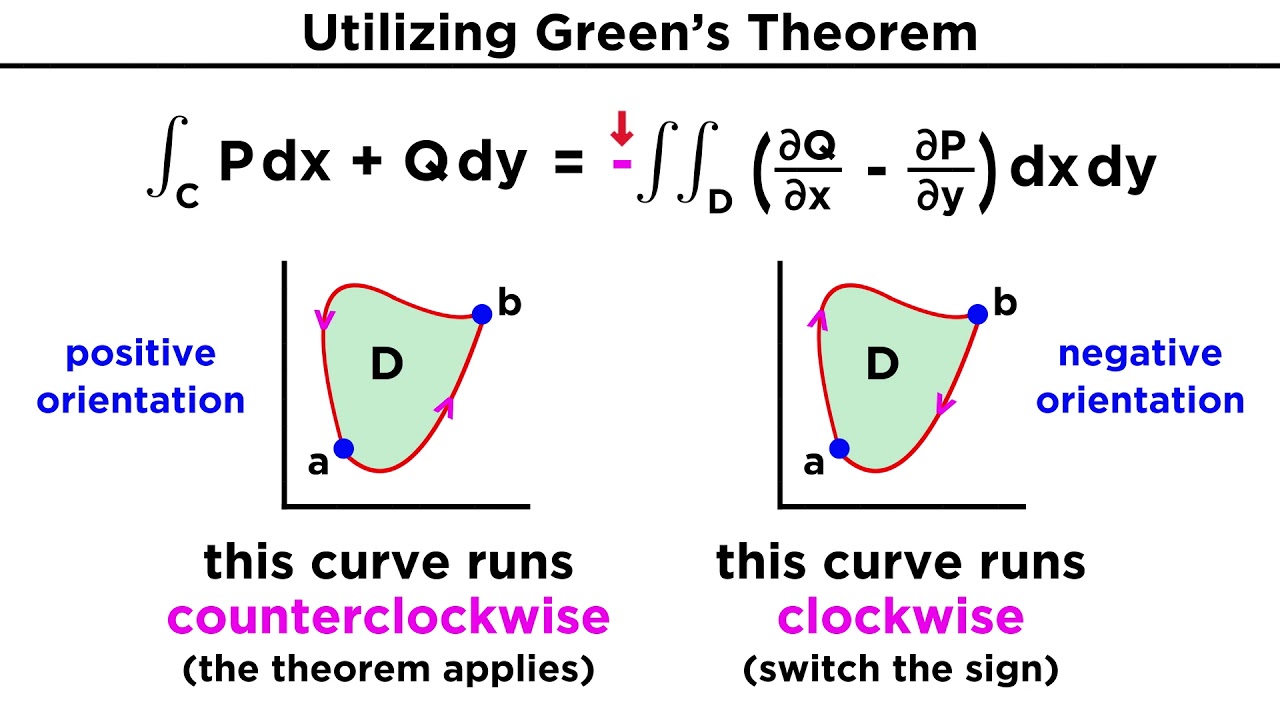
🔄 The direction of the path taken around the region is crucial; counterclockwise direction means the region is to the left.
📐 The line integral is represented as ∮(c) of f · dr, where f is a vector field and c is the curve.
🌀 The components of the vector field f are P(x, y) and Q(x, y), which are used to calculate the line integral.
🛤️ The boundary of the region is defined by the curve c, with specific conditions for x and y values.
📈 The integral to solve is given as x^2 - y^2 dx + 2xy dy over the boundary of the region.
📝 The region is sketched with x ranging from 0 to 1 and y ranging from 2x^2 to 2x.
🤔 Green's theorem can be applied directly if the inside of the region is to the left of the path taken.
🧠 The application of Green's theorem involves finding the partial derivatives of P and Q with respect to x and y.
📊 The final answer is obtained by evaluating the double integral over the region, which in this case is 16/15.
🎓 Understanding and applying Green's theorem is essential for solving complex line integrals and vector calculus problems.

Q & A

What is Green's theorem and how does it apply to line integrals?
-Green's theorem is a fundamental result in vector calculus that relates a line integral around a closed curve to a double integral over a region enclosed by the curve. It states that the line integral of a vector field around a closed curve is equal to the double integral of the divergence of the vector field over the region enclosed by the curve. This theorem is particularly useful in transforming difficult line integrals into easier-to-calculate double integrals.
How does the direction of traversal around a region affect the application of Green's theorem?
-The direction of traversal around a region is crucial when applying Green's theorem. If the region is traversed counterclockwise and the interior of the region is to the left of the path, then Green's theorem can be applied directly. However, if the direction of traversal is clockwise, a minus sign is introduced in the application of Green's theorem. This is because reversing the direction of the line integral changes the sign of the integral.
What is the significance of the vector field components P(x, y) and Q(x, y) in Green's theorem?
-In Green's theorem, P(x, y) and Q(x, y) represent the components of the vector field F. The vector field F is expressed as P(x, y)i + Q(x, y)j. These components are crucial as they are used to calculate the line integral along the curve and in the application of Green's theorem to transform it into a double integral.
How is the boundary of the given region defined in the script?
-The boundary of the region is defined by the set of points (x, y) such that x is greater than or equal to 0 and less than or equal to 1, and y is greater than or equal to 2x^2 and less than or equal to 2x. This boundary forms a closed curve that encloses a region which is to the left when traversed counterclockwise.
What is the integral being solved in the example provided in the script?
-The integral being solved is given by ∫(x^2 - y^2) dx + ∫(2xy) dy around the boundary of the defined region.
What are the expressions for P(x, y) and Q(x, y) in the given example?
-In the given example, P(x, y) is x^2 - y^2 and Q(x, y) is 2xy. These expressions are used to calculate the line integral according to Green's theorem.
How is the partial derivative of Q with respect to x calculated in the example?
-The partial derivative of Q with respect to x, denoted as ∂Q/∂x, is calculated as 2y. This is done by taking the derivative of the function Q(x, y) = 2xy with respect to x.
How is the partial derivative of P with respect to y calculated in the example?
-The partial derivative of P with respect to y, denoted as ∂P/∂y, is calculated as -2y. This is done by taking the derivative of the function P(x, y) = x^2 - y^2 with respect to y.
What is the result of the double integral over the region using Green's theorem in the example?
-The result of the double integral over the region using Green's theorem is 16/15. This is obtained by evaluating the integrals of the transformed expressions (∂Q/∂x - ∂P/∂y) over the region enclosed by the curve.
How does the process of evaluating the double integral using Green's theorem simplify the calculation?
-The process of evaluating the double integral using Green's theorem simplifies the calculation by transforming a potentially complex line integral into a double integral over a region. This often makes the problem easier to solve, as it allows us to use the properties of multiple integrals and avoid dealing with the intricacies of the path of integration.
What is the significance of the region being to the left of the path when traversed counterclockwise?
-The condition that the region is to the left of the path when traversed counterclockwise ensures that the line integral and the double integral have the same sign, allowing for the direct application of Green's theorem without the need for a minus sign. This simplifies the calculation and makes the theorem more straightforward to use.

Outlines

00:00

📚 Introduction to Green's Theorem and Problem Setup

This paragraph begins with a discussion on Green's theorem and its application to line integrals. The speaker clarifies that in previous examples, the region of interest was always to the left of the path traversed, which is a necessary condition for Green's theorem to apply. The paragraph then introduces a new problem where the goal is to compute a line integral along a closed path, with the integrand being x^2 - y^2 dx + 2xy dy. The boundary of the region is defined by the inequalities x ≥ 0, x ≤ 1, y ≥ 2x^2, and y ≤ 2x. The speaker emphasizes that the path is traversed in a counterclockwise direction, ensuring that the region remains to the left, which is consistent with the requirements of Green's theorem.

05:02

📈 Applying Green's Theorem to the Given Problem

In this paragraph, the speaker proceeds to apply Green's theorem to the previously defined problem. The function f(x, y) is defined as f = (x^2 - y^2)i + (2xy)j, and the speaker outlines the process of converting the line integral into a double integral over the region R. The speaker then sets up the necessary calculations by identifying the partial derivatives of the components of f with respect to x and y. The process involves taking the derivative of the y-component of f with respect to x, and the derivative of the x-component of f with respect to y, and then applying the fundamental theorem of calculus to evaluate the double integral. The speaker also discusses the importance of the direction of the path in relation to the region and how reversing the direction would result in a change of sign in the application of Green's theorem. The calculations are set up in a way that takes advantage of the natural setup for an indefinite integral, with the x boundary ranging from 0 to 1 and the y boundary varying between 2x^2 and 2x.

10:03

🧮 Completing the Calculation and Summarizing the Results

The final paragraph is dedicated to completing the calculations and summarizing the results. The speaker calculates the double integral by first integrating with respect to y, then x, and applying the boundaries of the region. The integral is broken down into simpler parts, with the speaker carefully walking through each step of the calculation. After evaluating the antiderivative of the function with respect to y and applying the x boundaries, the speaker then integrates with respect to x and evaluates the resulting antiderivative at the given boundaries. The final step involves combining the results of the x and y integrations to find the total value of the line integral. The speaker catches a mistake in the calculation, corrects it, and provides the final answer of 16/15 for the line integral. The paragraph concludes with a brief recap of the process and the utility of Green's theorem in solving the problem, highlighting that it was a successful application of the theorem to find the answer to the integral.

Mindmap

Keywords

💡Green's theorem

Green's theorem is a fundamental concept in vector calculus that relates a line integral around a closed loop to a double integral over the region enclosed by the loop. In the video, the theorem is used to calculate the line integral of a function along a curve by transforming it into a surface integral over the enclosed region. This is particularly useful when dealing with complex integrals that are difficult to evaluate directly.

💡line integrals

Line integrals are a type of mathematical integral where the integrand is evaluated along a curve or a line in the plane or in space. They are used to calculate quantities such as the work done by a force moving along a path or the flux of a vector field through a curve. In the context of the video, line integrals are used to set up the problem that will be solved using Green's theorem, illustrating the process of converting a difficult line integral into a more manageable form through the application of the theorem.

💡counterclockwise

Counterclockwise refers to the direction of traversing a path or curve in a manner that keeps the region of interest on the left side. This term is important in the context of Green's theorem because the orientation of the path (clockwise or counterclockwise) affects the sign of the line integral and the corresponding double integral. In the video, the author clarifies that all previous examples were solved with a counterclockwise orientation, which is the default situation for applying Green's theorem without any modifications.

💡region

In the context of the video, a region refers to the area enclosed by a curve or a set of curves. The region is the area over which the double integral is calculated when applying Green's theorem. It is essential to define the boundaries and the orientation of the region correctly to ensure the accurate application of the theorem.

💡components of f

In the context of vector calculus, the components of a vector function f, often denoted as P(x, y)i + Q(x, y)j, represent the x and y parts of the vector field, respectively. These components are crucial when applying Green's theorem, as they are used to form the integrand for the line integral and the partial derivatives for the double integral.

💡partial derivatives

Partial derivatives are derivatives that deal with the rate of change of a multivariable function with respect to one variable while keeping the other variables constant. They are essential in Green's theorem as they appear in the formula for transforming a line integral into a double integral over a region.

💡antiderivative

An antiderivative, also known as an indefinite integral, is a function whose derivative is the given function. In the context of the video, finding the antiderivative of an expression is necessary to evaluate the double integral resulting from applying Green's theorem.

💡curve

In mathematics, a curve is a one-dimensional continuous object in a two-dimensional space, defined by a function or a set of functions. In the video, the curve represents the boundary of the region over which the line integral is taken and is essential for setting up the problem using Green's theorem.

💡direction

Direction in the context of the video refers to the orientation of the path or curve along which the line integral is taken. The direction is important for determining the sign of the integral and the correct application of Green's theorem.

💡double integral

A double integral is an integral that involves the calculation of the integral of a function over a two-dimensional region. It is used to find the volume under a surface or the area of a surface in three-dimensional space. In the video, the double integral is the result of applying Green's theorem, which transforms a line integral into a double integral over the enclosed region.

Highlights

The application of Green's theorem in solving line integrals is discussed.

Clarification on the direction of the path in relation to the region for Green's theorem is provided.

Examples of how Green's theorem is applied when the region is to the left of the path are given.

The mathematical expression for a closed line integral along a curve is presented.

The components of the vector field f in relation to Green's theorem are explained.

The impact of the direction of the path on the sign of the line integral is discussed.

A specific problem involving a line integral and a defined curve is introduced.

The boundary of a region is mathematically defined with x and y conditions.

A visual representation of the region and its boundary is provided.

The conditions for applying Green's theorem directly are explained.

The process of applying Green's theorem to the given problem is detailed step by step.

The calculation of the partial derivatives of P and Q with respect to x and y is shown.

The integration process over the region R using Green's theorem is outlined.

The antiderivative of the function with respect to y is calculated.

The evaluation of the integral over the boundary of the region is performed.

The final answer to the line integral problem using Green's theorem is provided.

The practical application of Green's theorem in solving complex integrals is demonstrated.

Transcripts

Browse More Related Video

Green's theorem example 2 | Multivariable Calculus | Khan Academy

Green's Theorem, explained visually

Green's Theorem

Green's theorem proof part 1 | Multivariable Calculus | Khan Academy

Stokes' theorem proof part 6 | Multivariable Calculus | Khan Academy

Green's theorem proof (part 2) | Multivariable Calculus | Khan Academy

Green's theorem example 1 | Multivariable Calculus | Khan Academy

Takeaways

Q & A

What is Green's theorem and how does it apply to line integrals?

How does the direction of traversal around a region affect the application of Green's theorem?

What is the significance of the vector field components P(x, y) and Q(x, y) in Green's theorem?

How is the boundary of the given region defined in the script?

What is the integral being solved in the example provided in the script?

What are the expressions for P(x, y) and Q(x, y) in the given example?

How is the partial derivative of Q with respect to x calculated in the example?

How is the partial derivative of P with respect to y calculated in the example?

What is the result of the double integral over the region using Green's theorem in the example?

How does the process of evaluating the double integral using Green's theorem simplify the calculation?

What is the significance of the region being to the left of the path when traversed counterclockwise?