Stokes's Theorem
TLDRStokes's Theorem relates a line integral over a closed curve to a surface integral over the surface bounded by that curve. Much like Green's Theorem in 2D, it allows conversion between a line integral and a surface integral, but now in 3D. After defining key concepts like positively oriented curves and vector fields, the theorem is stated - relating the line integral of a vector field over a closed curve C to the surface integral of the curl of that field over the surface S bounded by C. An example is then worked through step-by-step, evaluating a line integral using Stokes's Theorem by first finding the appropriate surface integral. This demonstrates the theorem's ability to enable simpler integral calculations.
Takeaways
- 😀 Stokes's Theorem relates line integrals to surface integrals - it converts a line integral over a closed curve C into a surface integral over the surface S bounded by C
- 🧮 The theorem states: ∫C F.dr = ∫∫S (∇ x F).n dS - relating the line integral of F along C to the surface integral over S of the curl of F dot the normal vector n
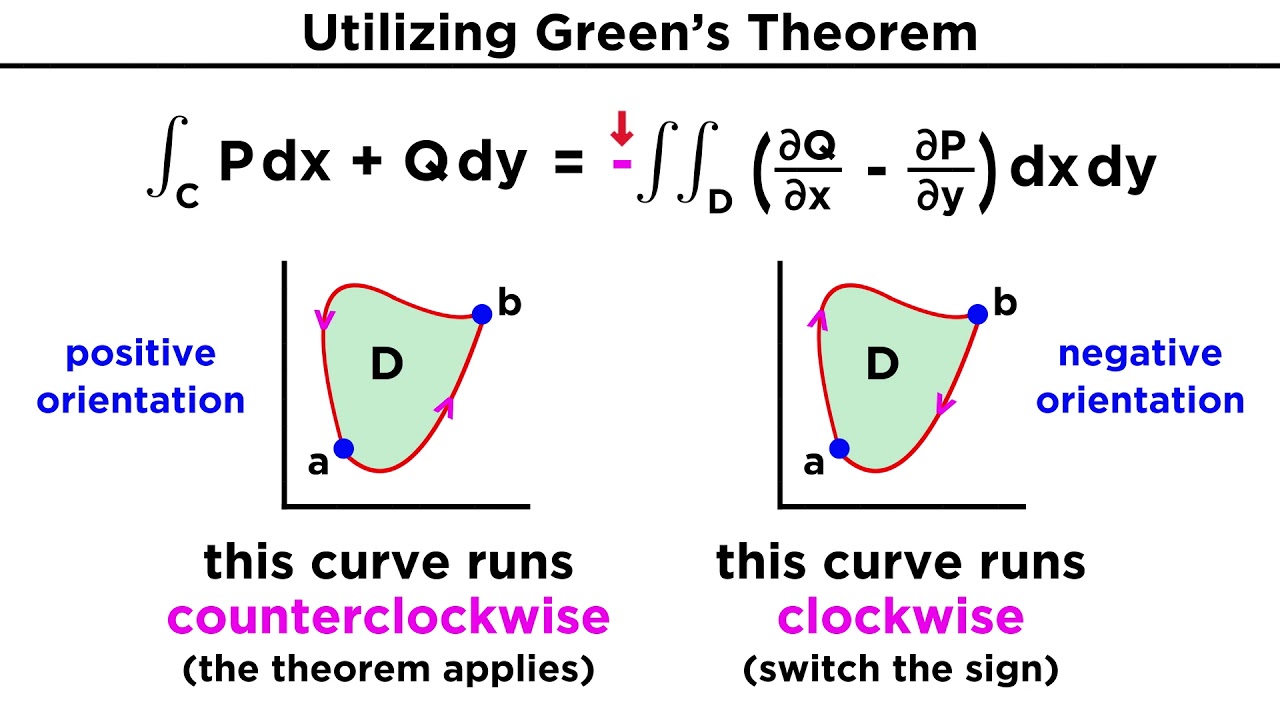
- 📏 It generalizes Green's Theorem to 3D, allowing calculations of line integrals in 3D space by converting them to surface integrals
- 🔢 It can simplify line integral calculations when the surface or bounds are simpler than directly evaluating the line integral
- 🧩 The example shows how Stokes's Theorem is applied - by parameterizing the surface, finding its derivatives, taking the curl of F, and evaluating the surface integral
- 🤓 Conceptually, Stokes's Theorem sums up the flux through an enclosed surface - the surface integral equals the net flow along the boundary
- ⚙️ The key steps are: find a surface S bounded by C; parameterize S; take curl of F; evaluate surface integral using Stokes's Theorem equation
- 📐 Geometrically, it links a surface integral (over S) to a line integral (over C) when C is the boundary of S
- 🔎 It can also be used in reverse - to find surface integrals when we know the line integral and boundaries
- 🧮 Overall, Stokes's Theorem is an important analytical tool relating line and surface integrals in multivariable calculus
Q & A
What does Stokes's Theorem allow us to do?
-Stokes's Theorem allows us to turn a line integral along a closed curve C in three dimensions into a surface integral over the surface S bounded by C. This can lead to simpler calculations.
What is the analogy between Stokes's Theorem and Green's Theorem?
-Green's Theorem relates a line integral along a closed curve in two dimensions to a double integral over the region bounded by the curve. Similarly, Stokes's Theorem relates a line integral along a closed curve in three dimensions to a surface integral over the surface bounded by the curve.
What does it mean for a curve C to be positively oriented?
-A positively oriented curve C means that as we traverse the curve, we travel in the counterclockwise direction with respect to the outward pointing normal vector of the surface S bounded by C.
What information is needed to set up the bounds of integration for Stokes's Theorem?
-To set up the bounds of integration, we need information about the surface S over which we are integrating. Specifically, we need a parametric or explicit representation of S in order to determine the range of the variables to integrate over.
How do you calculate the curl of a vector field F?
-The curl of F, denoted del x F, is calculated by taking the determinant of the matrix formed by the partial derivatives of the components of F. For example, if F = <Fx, Fy, Fz>, then curl F = i(∂Fz/∂y - ∂Fy/∂z) + j(∂Fx/∂z - ∂Fz/∂x) + k(∂Fy/∂x - ∂Fx/∂y).
What is the significance of Stokes's Theorem?
-Stokes's Theorem is significant because it links the fundamental concepts of line, surface, and volume integration through a simple and elegant equation. It allows conversions between integrals and provides alternate approaches to evaluate difficult integrals.
What information is provided by the triangle connecting (1,0,0), (0,1,0) and (0,0,1)?
-This triangle lies in the plane x + y + z = 1. Knowing the plane equation is useful for parameterizing the surface over which we will integrate.
How did we determine the bounds of integration?
-Looking at the triangular region in the xy-plane, we saw it was bounded by the line y = 1 - x between (1,0) and (0,1). We integrated y first from 0 to 1 - x, and x from 0 to 1 based on the endpoint coordinates.
What is the significance of the normal vector in Stokes's Theorem?
-The normal vector n allows us to integrate the curl F dotted with n over the surface S. This gives the component of curl F perpendicular to S, which is relevant for the line integral around the boundary curve C.
What are some examples of surfaces where Stokes's Theorem would be applicable?
-Stokes's Theorem can be applied to any oriented surface S with a closed boundary curve C. Some examples are spheres, cubes, ellipsoids, cylinders, cones, toruses, and anySurface created by revolving a planar curve around an axis.
Outlines
📐 Introducing Stokes's Theorem for Line Integrals
This paragraph introduces Stokes's Theorem, which allows conversion of a line integral over a closed curve C bounding a surface S into a surface integral over S. It states that the line integral of vector field F along curve C equals the surface integral of the curl of F over surface S. An example shows how Stokes's Theorem is applied to evaluate a line integral over a triangular region using a simpler surface integral calculation.
🔢 Applying Stokes's Theorem to Calculate a Line Integral
This paragraph works through an example application of Stokes's Theorem to calculate the line integral of a vector field F over a triangular curve C bounding the plane x+y+z=1. The surface integral formulation with bounds is set up and evaluated to determine the line integral via Stokes's Theorem, yielding a final value of -2/3. The paragraph concludes by noting that Stokes's Theorem allows choice of the simplest method to calculate certain line and surface integrals.
Mindmap
Keywords
💡Stokes's Theorem
💡line integral
💡surface integral
💡curl
💡delaunay triangulation
💡vector field
💡parametrization
💡surface normal
💡gradient
💡flux
Highlights
Stokes's Theorem allows us to calculate line integrals over closed curves by converting them to surface integrals, which can simplify calculations.
The theorem equates the line integral of a vector field F over a closed curve C to the surface integral of the curl of F over any surface S bounded by C.
We can use Stokes's Theorem in reverse to find surface integrals when the boundary curve C is simple enough to directly calculate.
We applied Stokes's Theorem to a triangle in 3D space defined by points (1,0,0), (0,1,0) and (0,0,1), using a parametric surface.
We had to calculate the curl of the vector field F, take cross products with surface partial derivatives, and set up the double integral.
The final integral simplified to (x^2 - 1) dx, which we could directly integrate over the triangular region.
The line integral result came out to be -2/3, a simpler calculation than directly integrating F.
Stokes's Theorem connects line, surface and volume integrals in multivariable calculus.
It allows conversions between integrals when one form simplifies calculations.
The theorem generalizes Green's Theorem to higher dimensions just as the Fundamental Theorem of Calculus generalizes integration rules.
The curl operation in Stokes's Theorem captures the rotation or circulation of a vector field around a region.
The direction of surface orientation and curve parameterization must align for the theorem to work correctly.
Real-world applications include fluid dynamics, electromagnetism, and analyzing vector fields in space.
While simple cases demonstrate the concept, most applications require deeper understanding to set up and interpret properly.
Stokes's Theorem is a gateway into advanced theoretical and applied mathematics in multivariate settings.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: