Green's theorem proof (part 2) | Multivariable Calculus | Khan Academy
TLDRThe video script discusses the concept of line integrals and vector fields, focusing on how a line integral around a closed loop can be transformed into a double integral over a region. It introduces the specific case where the vector field has components only in the i and j directions, and explains how to calculate the line integral by breaking it down into simpler parts. The script then connects this to Green's Theorem, which relates the line integral of a vector field to a double integral over a region, and discusses the implications for conservative vector fields. The explanation is clear, methodical, and builds upon concepts from previous videos to provide a comprehensive understanding.
Takeaways
- 📐 The script discusses the concept of line integrals and vector fields, specifically focusing on their application in the context of a curve 'c' and a vector field 'q'.
- 🔄 The line integral around a closed loop can be transformed into a double integral over a region, which is a key application of Green's Theorem.
- 🤔 The vector field 'q' considered in the script has only a vertical (j-direction) component, which simplifies the line integral to an integral over 'y'.
- 📈 The script demonstrates the process of breaking down a complex integral into simpler parts by considering the minimum and maximum values of 'y' and defining two paths based on these extreme points.
- 🌐 The concept of parameterization is introduced, where 'x' is expressed as a function of 'y', which is a switch from the usual 'y' as a function of 'x'.
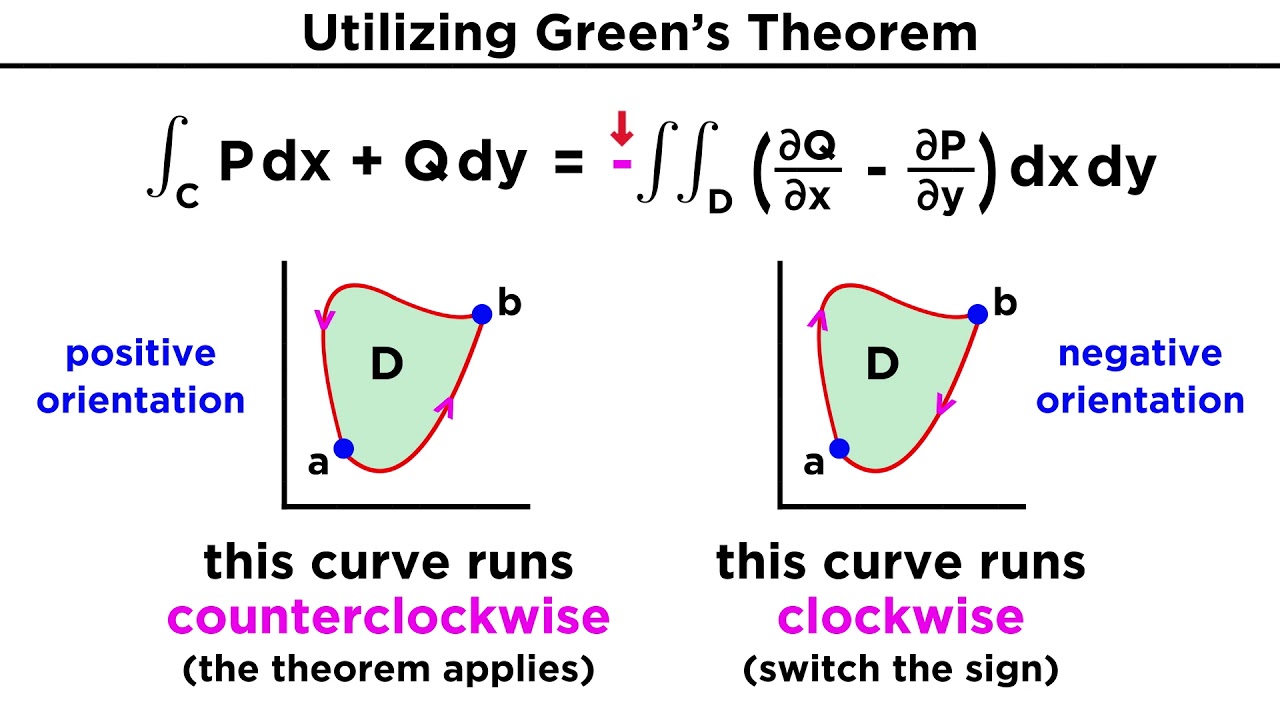
- 🔄 The direction of the curve is important and is specified as counterclockwise, which affects how the integral is computed.
- 📊 The script visually represents the idea of a differential area 'da', which is the product of differentials 'dx' and 'dy', and is used to define the region over which the double integral is taken.
- 🔢 The result of the line integral is equivalent to the double integral of the partial derivative of Q with respect to x, minus the partial derivative of P with respect to y, over the defined region.
- 🔄 The script emphasizes the symmetry and relationship between the line integral and double integral, showing that the order of integration can be reversed.
- 🌟 Green's Theorem is introduced as a powerful tool to convert a line integral around a closed loop into a double integral over a region, provided the vector field has continuous partial derivatives.
- 🔍 The implications of a conservative vector field are discussed, stating that if the vector field is conservative, the line integral around any closed path must be zero, leading to important conclusions in the study of differential equations.
Q & A
What is the main concept discussed in the video?
-The main concept discussed in the video is the calculation of line integrals in the context of vector fields, specifically focusing on the transformation of line integrals into double integrals using the concepts from Green's Theorem.
How does the video relate to a previous video?
-The video builds upon the concepts introduced in a previous video, where the focus was on vector fields with vectors only in the i-direction. It extends the understanding to cases where the vector field has components in the j-direction as well.
What is the significance of the vector field q having only a j-component?
-The significance of the vector field q having only a j-component is that it simplifies the line integral calculation. Since q has no i-component, the dx term drops out, leaving only Q*dy, which makes the integral easier to compute.
What is the role of the parameter t in the context of this video?
-In the context of this video, the parameter t is not explicitly mentioned as the focus is on solving the line integral without resorting to a third parameter. The video aims to find a solution by dealing with y's now instead of x's, as was done in the previous video.
What is the significance of the curve c in the video?
-The curve c represents the path in the xy-plane along which the line integral is being computed. It is a specific curve that was also used in the last video, and the video assumes that the viewer is familiar with its properties and the direction of traversal, which is counterclockwise.
How does the video approach the calculation of the line integral of q dot dr?
-The video approaches the calculation by expressing the differential dr as a combination of dx times i and dy times j. It then uses the fact that the vector field q only has a j-component to simplify the dot product to Q*xy times dy. The video then discusses how to solve this line integral without introducing a third parameter, t.
What is the significance of the functions x1(y) and x2(y) in the video?
-The functions x1(y) and x2(y) represent the upper and lower boundaries of the region over which the y-variable varies. They are used to define the path in terms of y, which is crucial for the transformation of the line integral into a double integral.
How does the video connect the line integral to a double integral?
-The video connects the line integral to a double integral by breaking the path into two parts and expressing these parts as functions of y. It then shows that the line integral can be rewritten as the sum of two definite integrals, which can be combined into one double integral over the region defined by the path c and the boundaries x1(y) and x2(y).
What is the geometric interpretation of the double integral in the context of the video?
-The geometric interpretation of the double integral in the context of the video is the volume of the region defined by the path c and the boundaries x1(y) and x2(y). It represents the integral of the function Q over this region, which can be thought of as the volume enclosed by the curve c and the vertical lines defined by x1(y) and x2(y).
How does the video relate the line integral of a vector field to Green's Theorem?
-The video relates the line integral of a vector field to Green's Theorem by showing that the closed line integral of a vector field F around a path is equal to the double integral of the region enclosed by the path. Specifically, it shows that the integral of the j-component of the vector field (Q) is related to the double integral of ∂Q/∂x, and the integral of the i-component (P) is related to the double integral of -∂P/∂y over the enclosed region.
What is the implication of the vector field F being conservative?
-If the vector field F is conservative, it implies that it is the gradient of some scalar function, and hence, the closed line integral around any path is equal to zero. This leads to the conclusion that for F to be conservative, the partial derivative of Q with respect to x must be equal to the negative of the partial derivative of P with respect to y over the entire region.
Outlines
📐 Introduction to Vector Fields and Line Integrals
The paragraph introduces the concept of vector fields and line integrals. It begins with a discussion of a specific path and curve, similar to those in a previous video. The focus is on a vector field, denoted as 'q', which has components only in the j (vertical) direction. The line integral of 'q' around a path 'c' is explored, with an emphasis on the dot product of 'q' and 'dr'. The integral is broken down into its components, highlighting that 'q' only has a j-component, leading to an integral in terms of 'dy'. The goal is to solve this line integral without introducing a third parameter, 't', and the approach is compared to a similar problem from a previous video.
📊 Transformation of Integrals and Path Boundaries
This paragraph delves into the transformation of integrals and the concept of path boundaries. It discusses breaking the line integral into two parts, corresponding to minimum and maximum 'y' values, denoted as 'a' and 'b'. The direction of the curve is specified as counterclockwise. The paragraph then explores expressing 'x' as a function of 'y', which is analogous to the previous video's approach but with swapped variables. The line integral is rewritten in terms of 'y', and the process of integrating over the two paths is explained. The result is a single definite integral from 'a' to 'b', involving the functions 'x1(y)' and 'x2(y)'.
🌐 Interpretation of Double Integrals and Vector Fields
The paragraph discusses the interpretation of double integrals in the context of vector fields. It describes the double integral as a representation of volume, with the vector field 'Q' having only a vertical component. The line integral around a closed loop is related to the double integral over a region, with the region defined by the boundaries 'x1(y)' and 'x2(y)', and 'y' ranging from 'a' to 'b'. The paragraph emphasizes the equivalence of the line integral and the double integral, and how the double integral can be visualized as the volume of a room with 'x1(y)' and 'x2(y)' as walls and 'y' as the ceiling.
📚 Green's Theorem and Its Implications
This paragraph presents Green's Theorem and its implications for vector fields. It concludes that the line integral of a closed loop of a vector field 'F' is equal to the double integral of the region, which is the difference between the partial derivatives of the vector field's components with respect to 'x' and 'y'. The theorem is expressed as an integral formula, and the paragraph highlights the significance of this result. It also discusses the implications of Green's Theorem for conservative vector fields, noting that if 'F' is conservative, the expression must integrate to zero over any region. The relationship between conservative fields, exact equations, and Green's Theorem is briefly touched upon, suggesting further exploration in differential equations.
Mindmap
Keywords
💡Vector Field
💡Line Integral
💡Dot Product
💡Partial Derivatives
💡Green's Theorem
💡Conservative Field
💡Path Independence
💡Double Integral
💡Differential Form
💡Exact Equation
💡Closed Loop
Highlights
The discussion begins with a review of the previous video's content, setting the stage for a deeper exploration of vector fields and line integrals.
The introduction of a new vector field 'q' that only has vectors in the j (vertical) direction, which is a shift from the previous focus on the i (horizontal) direction.
The methodical approach to solving the line integral without a third parameter 't', similar to the technique used in the last video, but applied to 'y's' instead of 'x's'.
The concept of breaking the path into two functions of y, which is analogous to the previous video's approach but now expressed in terms of 'x as a function of y'.
The detailed explanation of how to express the line integral in terms of a double integral by considering the boundaries of integration and the direction of the curve.
The demonstration of how the line integral can be rewritten as the integral from b to a of Q of x2 of y, dy, and then adding the integral from a to b of Q of x1 of y, dy.
The clear distinction between the 'i' and 'j' components of the vector field and how they contribute to the line integral.
The creative visualization of the line integral as a volume within a defined region, emphasizing the relationship between the vector field and the enclosed area.
The explanation of how the double integral represents the volume of a room with the boundary acting as the wall and the ceiling, providing a tangible understanding of the concept.
The transition from discussing the specific vector field 'q' to an arbitrary vector field 'F' defined over the xy plane, expanding the scope of the discussion.
The formulation of Green's Theorem as a conclusion, relating the line integral of a vector field to a double integral over a region.
The explanation of how the line integral is path-independent if the vector field is conservative, leading to the condition that the partial of Q with respect to x must equal the partial of P with respect to y.
The mention of the potential for further exploration of these concepts in the context of differential equations, hinting at the broader applications of the discussed methods.
The proposal to apply the insights from this discussion to examples in the next video, encouraging continued learning and application of the concepts.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: