Green's theorem proof part 1 | Multivariable Calculus | Khan Academy
TLDRThe video script discusses the concept of line integrals in the context of a vector field with only an i-component, represented as p of xy. It illustrates how to calculate the line integral over a closed loop, c, by breaking the path into two functions of x and then simplifying the integral. The script creatively transitions the line integral into a double integral over a region, r, by relating it to the partial derivative of P with respect to y. This insightful exploration establishes a connection between line integrals and double integrals, ultimately hinting at the upcoming discussion of Green's theorem.
Takeaways
- 📐 The concept introduces a path (c) in the xy-plane and a vector field (p) with only an i-component.
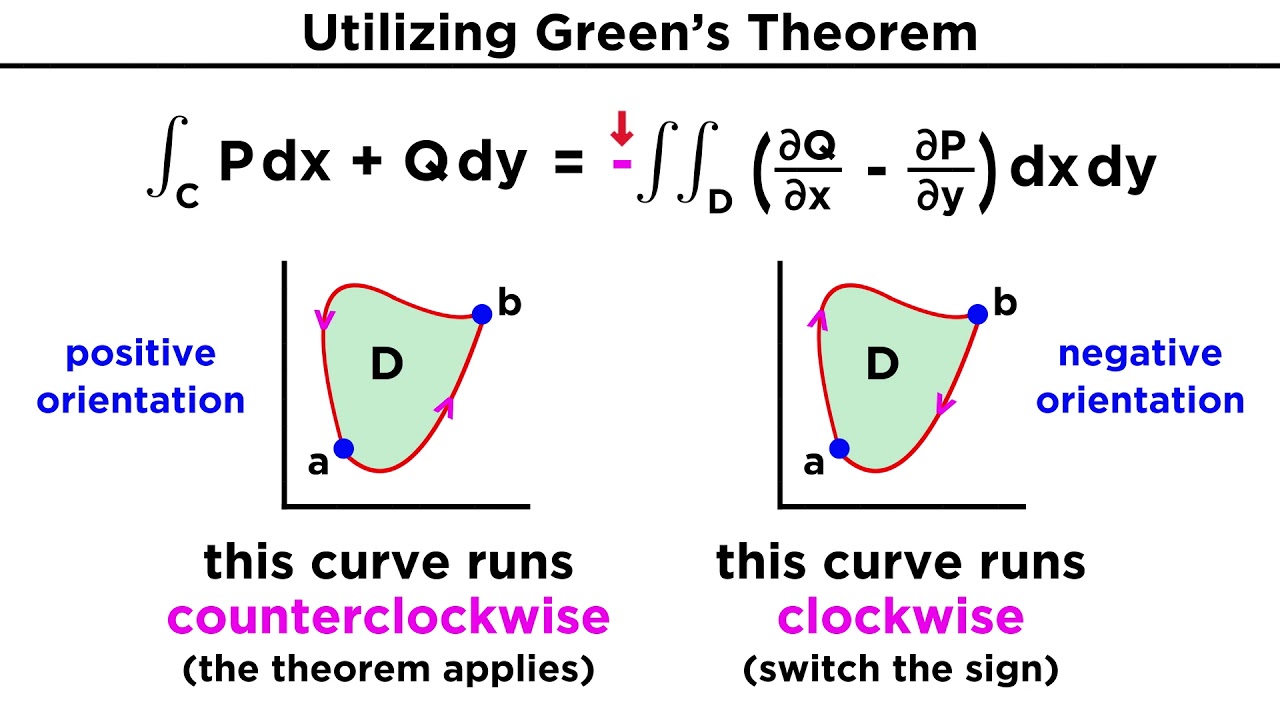
- 🔄 The path c is traversed in a counter-clockwise direction, and the vector field p has vectors that are multiples of the i-unit vector.
- 🧮 The line integral over the closed loop c is calculated as the integral of p dot dr, where dr is dx times i plus dy times j.
- 📈 The integral can be simplified by considering the path c as the union of two functions of x, y1(x) and y2(x), and breaking the integral into two parts.
- 🔄 By swapping the end points of the integral and changing the sign, the line integral can be rewritten as an integral from a to b of [p(x, y1(x)) - p(x, y2(x))] dx.
- 🌀 The process involves multiplying the integral by -1 inside and outside to rearrange the terms without changing the value of the integral.
- 📊 The integral can be further transformed into a double integral over a region r on the xy-plane, where the boundaries are defined by y2(x) and y1(x).
- 🧠 The double integral is equivalent to the negative of the line integral, and it represents the volume under the surface defined by the partial derivative of P with respect to y.
- 🌐 The region r is defined by the area enclosed by the curve c and the height given by the function p(x, y).
- 🔄 The video script demonstrates the conversion of a line integral in the context of a vector field into a double integral, which is a fundamental concept in vector calculus.
- 📚 The final outcome connects the line integral of a vector field with only an x-component to a double integral over a specific region, laying the groundwork for further exploration of Green's theorem.
Q & A
What is the main topic discussed in the transcript?
-The main topic discussed in the transcript is the concept of line integrals in the context of a vector field with only an i-component, and how it can be simplified and related to double integrals.
What does the vector field 'p' represent in the transcript?
-In the transcript, the vector field 'p' represents a field with only an i-component, meaning all its vectors are multiples of the i-unit vector, and there is no j-component involved.
How is the path 'c' described in the transcript?
-The path 'c' is described as an arbitrary path in the xy-plane, going in a counter-clockwise direction.
What is the differential 'dr' in the context of the line integral?
-In the context of the line integral, 'dr' is the differential vector which is equal to dx times i plus dy times the j-unit vector.
How does the speaker propose to simplify the line integral?
-The speaker proposes to simplify the line integral by breaking up the curve into two functions of x, and then rewriting the integral as the sum of two integrals, one for each function.
What is the significance of the minimum and maximum x points in the script?
-The minimum and maximum x points are significant because they define the boundaries for the two functions of x that are used to simplify the line integral.
How does the speaker connect the line integral to a double integral?
-The speaker connects the line integral to a double integral by rewriting it in a form that is equivalent to the partial derivative of P with respect to y, evaluated over a certain region in the xy-plane.
What is the significance of the negative sign in the final simplification?
-The negative sign in the final simplification indicates that the line integral is related to the double integral with a negative sign, which is an important aspect of the relationship between these two types of integrals in this specific context.
What theorem is hinted to be discussed in the next video?
-The transcript hints that the next video will discuss Green's theorem, which connects line integrals around a closed curve to double integrals over a region bounded by the curve.
How does the speaker's approach to explaining the concepts help in understanding?
-The speaker's approach of breaking down complex concepts into simpler parts and building up to the final result step by step helps in understanding by making the material more digestible and easier to follow.
Outlines
📐 Introduction to the Path and Vector Field
The video begins by introducing a path in the xy plane, with a focus on the x and y axes. An arbitrary path is drawn, moving in a counter-clockwise direction, and is designated as path c. A vector field, denoted as p, is also introduced, with the unique characteristic that it only has an i component, meaning all vectors are multiples of the i-unit vector. The video then sets up the problem of finding the line integral over the closed loop c of the vector field p dot dr, where dr is defined as dx times i plus dy times the j-unit vector. The goal is to solve this integral in terms of x alone, and the video outlines a strategy for doing so by examining the minimum and maximum x points of the path and breaking the curve into two functions of x, y1 and y2.
🔄 Solving the Line Integral by Breaking the Path into Functions
This paragraph continues the exploration of the line integral by breaking the curve into two parts, c1 and c2, each defined by a different function of x. The integral is then rewritten as the sum of two separate integrals, one for each part of the path. The video discusses the possibility of simplifying the integral further by making the endpoints of the two functions the same, which involves changing the signs of the integrals and combining them into a single integral from a to b. The process is visualized with the help of colors to differentiate between the two paths and their respective contributions to the integral. The paragraph concludes with a transformation of the integral into a form that resembles a double integral, setting the stage for the next part of the explanation.
📚 Connection Between Line Integral and Double Integral
The final paragraph ties the line integral to a double integral over a region r, which is defined by the boundaries of the curve in the xy plane. By assuming the existence of a partial derivative of the vector field p with respect to y, the video shows that the line integral can be transformed into the double integral of the partial of p with respect to y over the region r. This transformation is visualized by imagining the surface defined by the partial of p with respect to x and the volume under this surface bounded by the curve in the xy plane. The video emphasizes the novelty of this approach, which starts with the solution of the definite integral and works backward to the definition of the line integral. The conclusion is that the line integral around the curve c of the vector field p dot dr is equivalent to the double integral over the region r of the partial of p with respect to y, with a negative sign. This sets the stage for further exploration in the next video, where the concept will be extended to a vector field with a y-component, leading to Green's theorem.
Mindmap
Keywords
💡xy plane
💡counter clockwise
💡vector field
💡line integral
💡unit vector i
💡differential dr
💡minimum and maximum x points
💡path functions y1(x) and y2(x)
💡double integral
💡partial derivative
💡Green's theorem
Highlights
The discussion begins with the introduction of a path in the xy plane, setting the stage for the exploration of vector fields and line integrals.
An arbitrary path is drawn in the xy plane, representing the curve 'c' over which the line integral will be calculated.
A unique vector field 'p' is introduced, characterized by having only an i component, meaning all vectors are multiples of the i-unit vector.
The line integral over a closed loop is defined, using the standard notation p dot dr, which is central to solving the problem.
The differential dr is expressed in terms of dx and dy, simplifying the integral and focusing on the x and y variables.
The concept of breaking the curve into two functions of x, y1(x) and y2(x), is introduced to simplify the line integral.
The line integral is rewritten as the sum of two integrals, one for each function of x, showcasing a novel approach to solving complex integrals.
The end points of the integral are adjusted to simplify the expression, highlighting the importance of boundary conditions in integral calculus.
A creative step is taken by multiplying the entire expression by negative one, which allows for a new perspective on the integral.
The integral is then reformulated as a double integral, demonstrating the connection between line integrals and double integrals.
The existence of a partial derivative of the function P with respect to y is assumed, which is crucial for the next steps in the analysis.
The double integral is expressed as the volume under a surface defined by the partial derivative of P with respect to y, providing a geometric interpretation.
The line integral is shown to be equivalent to the double integral over a region R, marking a significant result in the context of vector calculus.
The negative sign in the final expression is highlighted, emphasizing the importance of sign conventions in mathematical analysis.
The video concludes with a mention of the next topic, which will involve vector fields with components in the y-direction and the introduction of Green's theorem.
Throughout the transcript, a clear and methodical approach to solving complex integral problems is demonstrated, which can be valuable for educational purposes.
The use of visual aids and color coding in the explanation helps to clarify the concepts and steps involved in the calculations.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: