Stokes' theorem proof part 7 | Multivariable Calculus | Khan Academy
TLDRThe script from a mathematical video tutorial delves into the application of Green's Theorem to convert a line integral around a boundary into a double integral over a region. It meticulously explains the process of taking partial derivatives of vector fields and applying the multi-variable chain rule. The goal is to demonstrate the equivalence of the line integral to a surface integral, which serves as a proof for Stokes' Theorem in a special case. The tutorial concludes with the successful simplification of the double integral, showing its identity to the original line integral.
Takeaways
- 📚 The video script discusses the application of Green's Theorem to convert a line integral around the boundary of a surface into a double integral over the region bounded by that surface.
- 🔍 The line integral \(f.dr\) along the boundary path \(c\) is expressed in terms of another line integral around the boundary path \(c1\), which is the boundary of region \(R\).
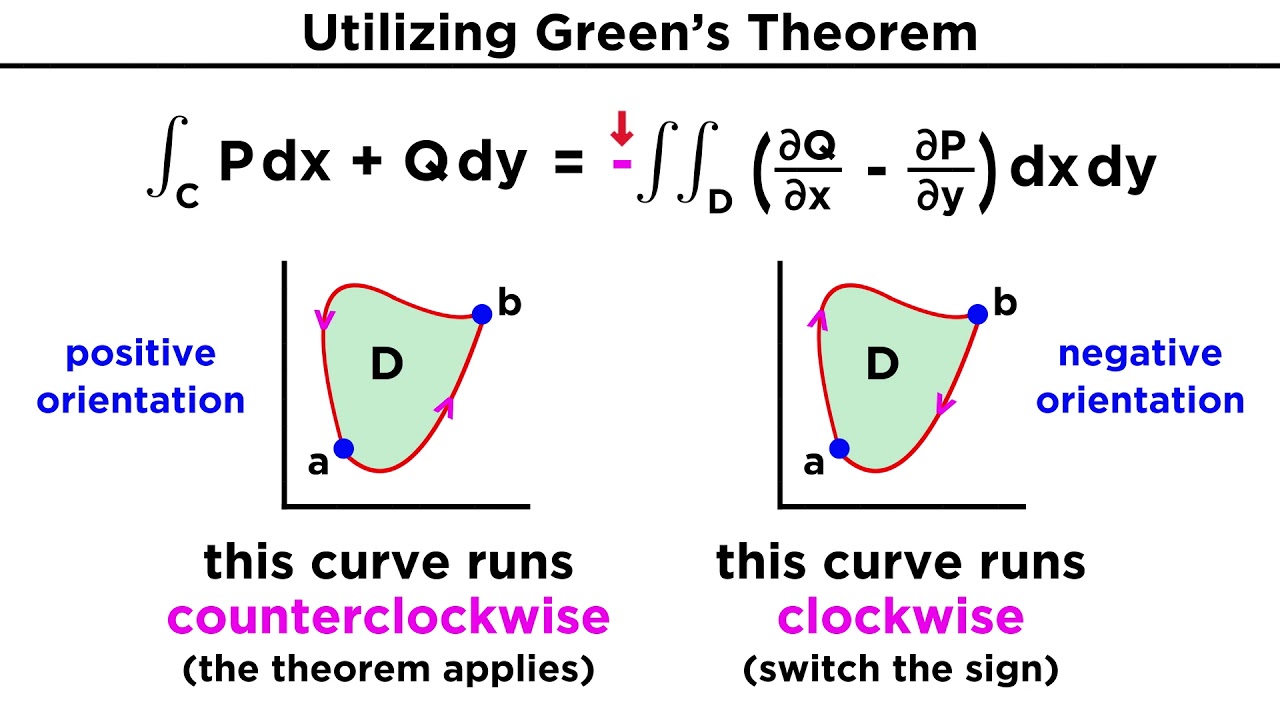
- 📈 Green's Theorem is applied to transform the line integral into a double integral involving partial derivatives of functions \(P\), \(Q\), and \(R\) with respect to \(x\) and \(y\).
- 🔧 The process involves taking partial derivatives using the multi-variable chain rule, considering that \(z\) is a function of \(x\) and \(y\), and how changes in \(x\) and \(y\) affect \(Q\) and \(R\).
- 📝 The script emphasizes the importance of correctly applying the product rule and the multi-variable chain rule in the calculation of partial derivatives.
- 🔄 The simplification of the double integral expression involves canceling out terms and grouping similar terms to make the comparison with the original line integral possible.
- 🧩 The script demonstrates that under the assumption of continuous second derivatives, certain terms in the double integral expression cancel each other out.
- 📉 The final expression of the double integral is compared to the original line integral, showing that they are identical for the special case discussed.
- 📚 The video aims to prove Stokes' Theorem for this special case by showing the equivalence of the line integral and the surface integral.
- 📝 The script provides a detailed algebraic manipulation of the double integral expression, highlighting the importance of careful expansion and simplification.
- 🎯 The conclusion of the video is that for the given special case, the line integral around the path \(c\) is equal to the surface integral over the region \(R\), thus confirming the application of Stokes' Theorem.
Q & A
What is the main topic discussed in the video script?
-The main topic discussed in the video script is the application of Green's Theorem to convert a line integral around the boundary of a surface into a double integral over the region bounded by the surface.
What is the significance of expressing the line integral in terms of the boundary of the region?
-The significance is that it allows for the direct application of Green's Theorem, which can then transform the line integral into a double integral over the region, simplifying the analysis of the problem.
What theorem is applied to the line integral to convert it into a double integral?
-Green's Theorem is applied to the line integral to convert it into a double integral over the region bounded by the path.
What does the partial derivative with respect to x of Q represent in the context of the script?
-It represents how Q changes directly with respect to x, as well as how Q could change due to changes in z, which is a function of x.
Why is the multi-variable chain rule necessary when taking the partial derivative of Q with respect to x?
-The multi-variable chain rule is necessary because Q is a function of x, y, and z, and z itself is a function of x. This rule accounts for the indirect changes in Q due to changes in z as x varies.
What is the role of the product rule in the script when differentiating expressions involving R and z?
-The product rule is used to differentiate expressions involving R and z because both R and z can change with respect to x, and the rule helps to account for the derivative of the product of these two functions.
How does the script simplify the expression for the double integral after taking the partial derivatives?
-The script simplifies the expression by canceling out terms that are negatives of each other and by grouping terms with common factors, such as the partial derivatives of z with respect to x and y.
What assumption is made about the function z in the script?
-The assumption made about the function z in the script is that it has continuous second derivatives and is a function of x and y.
How does the script demonstrate the equivalence of the line integral and the surface integral for a special case?
-The script demonstrates the equivalence by showing that after applying Green's Theorem and simplifying the resulting double integral, it matches the original line integral, thus proving the equivalence for the special case.
What is the final conclusion of the script regarding the relationship between the line integral and the surface integral?
-The final conclusion is that for the special case discussed, the line integral around the path c is equal to the surface integral over the region, which is a demonstration of Stokes' Theorem for this case.
Outlines
📚 Application of Green's Theorem to Line Integrals
This paragraph discusses the transition from a line integral around the boundary of a surface to a double integral over the region bounded by that surface. The application of Green's Theorem is explained, which allows the conversion of the line integral into a double integral over the region R. The paragraph emphasizes the importance of understanding how the functions P, Q, and R change with respect to x and y, and introduces the multi-variable chain rule in the context of partial derivatives. The goal is to show that for a special case, the line integral is equivalent to the surface integral, which is part of proving Stokes' Theorem.
🔍 Detailed Calculation of Partial Derivatives in Multivariable Context
The second paragraph delves into the specifics of calculating partial derivatives for the functions P, Q, R, and z, which are all functions of x, y, and z. It explains the use of the product rule and the multi-variable chain rule to find the partial derivatives with respect to x and y. The paragraph illustrates the process of expanding and simplifying the expressions to eventually obtain a form that can be compared to the original line integral. The focus is on the algebraic manipulation and the logical steps involved in the simplification process, aiming to show the cancellation of terms and the grouping of similar terms to simplify the double integral expression.
🎯 Conclusion of Line Integral Equivalence to Surface Integral
The final paragraph concludes the process by comparing the simplified form of the double integral obtained through the application of Green's Theorem and the multi-variable chain rule with the original line integral. It demonstrates that under the given assumptions of continuous second derivatives, the line integral and the surface integral are identical for the special case considered. This result supports the proof of Stokes' Theorem for this specific scenario, showing the equivalence of the two integrals and completing the demonstration.
Mindmap
Keywords
💡Line Integral
💡Green's Theorem
💡Partial Derivative
💡Multi-variable Chain Rule
💡Surface Integral
💡Stokes' Theorem
💡Differential Element 'dA'
💡Continuous Second Derivatives
💡Product Rule
💡Simplification
💡Commutative Property
Highlights
The line integral around the boundary of a surface is expressed in terms of a line integral around the boundary path c1.
Green's Theorem is applied to convert the line integral into a double integral over the region R bounded by c1.
The double integral involves the partial derivatives of functions P, Q, R with respect to x and y.
The multi-variable chain rule is used to take partial derivatives when z is a function of x and y.
The product rule is applied when differentiating expressions involving R and z_sub_y with respect to x.
The multi-variable chain rule is again utilized when differentiating with respect to y, considering the dependencies of P, R, and z on x and y.
The simplification process involves canceling out terms that are negatives of each other due to the continuous second derivatives of z.
The final simplified form of the double integral is obtained by grouping and factoring terms involving partial derivatives of z with respect to x and y.
The double integral is shown to be equivalent to the original line integral, demonstrating a special case of Stokes' Theorem.
The process emphasizes the importance of correctly applying calculus rules like the chain rule and product rule in multivariable calculus.
The transcript provides a detailed walkthrough of the mathematical steps involved in proving a special case of Stokes' Theorem.
The demonstration of the proof relies on the assumption of continuous second derivatives for the function z.
The transcript illustrates the power of Green's Theorem in simplifying complex integral problems in vector calculus.
The final result confirms the equality of the line integral and surface integral for the given case, solidifying the understanding of Stokes' Theorem.
The methodical approach to simplification and the clear explanation of each step make the complex proof accessible to learners.
The practical application of the proof is showcased through the comparison of the line integral and surface integral, highlighting the theorem's utility.
Transcripts
Browse More Related Video

Green's and Stokes' theorem relationship | Multivariable Calculus | Khan Academy

Stokes' theorem proof part 3 | Multivariable Calculus | Khan Academy

Green's theorem proof (part 2) | Multivariable Calculus | Khan Academy
Green's Theorem

Stokes' theorem proof part 6 | Multivariable Calculus | Khan Academy

Stokes' theorem proof part 5 | Multivariable Calculus | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: