Adding Vector Components Example | Physics with Professor Matt Anderson | M3-11
TLDRIn this instructional transcript, Professor Anderson guides students through the process of vector decomposition and composition. The example involves a journey with three legs: one mile north, 0.4 miles west, and 0.1 mile south. The professor explains how to represent each leg as a vector in the x-y coordinate system using unit vectors i (east) and j (north). The first vector (a) is purely vertical (1 j), the second (b) is westward (-0.4 i), and the third (c) is slightly south (0 j - 0.1). The resultant vector is found by summing the components, leading to a magnitude of 0.98 and an angle of approximately 23 degrees from the positive x-axis. The lesson emphasizes the importance of understanding vectors for calculating both magnitude and direction.
Takeaways
- 📝 The lesson focuses on vector decomposition, using unit vectors to break down and reassemble vectors.
- 🏃♂️ The example problem involves a journey: 1 mile north, 0.4 miles west, and 0.1 mile south.
- 📍 Vector A (a) is represented as 0î + 1ĵ, with no movement east or west and one mile north.
- 🔄 Vector B (b) is represented as -0.4î + 0ĵ, moving 0.4 miles west (negative x-direction).
- 🔽 Vector C (c) is represented as 0î - 0.1ĵ, with no movement east or west and 0.1 mile south.
- 🔜 The resultant vector (r) is found by summing the components of vectors A, B, and C, resulting in -0.4î + 0.9ĵ.
- 📐 The magnitude of vector r is calculated using the Pythagorean theorem, resulting in a length of 0.98.
- 📐 The angle with the x-axis (phi) can be found using trigonometric relations, in this case, arccos(0.9/0.98) yielding approximately 23 degrees.
- 🤔 Understanding the components of a vector allows for the calculation of its length and the determination of its direction.
- 👉 The process of vector decomposition is useful for analyzing and solving problems involving motion and displacement.
- 💡 This method can be applied to various vector problems, not limited to physical movement but also to other vector-based calculations.
Q & A
What is the main topic of the example problem discussed in the transcript?
-The main topic is the concept of breaking down vectors into their components using unit vectors and then adding them up to find the resultant vector.
How many segments are there in the journey described in the example problem?
-There are three segments in the journey: one mile to the north, 0.4 miles to the west, and 0.1 mile to the south.
What are the unit vectors used in the x and y directions as mentioned in the transcript?
-The unit vectors used are i_hat for the x direction (east axis) and j_hat for the y direction (north axis).
How is vector a represented in terms of unit vectors?
-Vector a is represented as 0i_hat + 1j_hat, indicating a movement of one mile directly north without any east-west component.
What is the representation of vector b in terms of unit vectors?
-Vector b is represented as -0.4i_hat + 0j_hat, indicating a movement of 0.4 miles to the west and no movement to the north or south.
How is vector c represented in terms of unit vectors?
-Vector c is represented as 0i_hat - 0.1j_hat, indicating no east-west movement and a movement of 0.1 mile to the south.
What is the resultant vector r obtained by adding vectors a, b, and c?
-The resultant vector r is obtained by adding the components of a, b, and c, which results in -0.4i_hat + 0.9j_hat.
How is the magnitude of the resultant vector calculated?
-The magnitude of the resultant vector is calculated by squaring each component, summing them up, and then taking the square root. In this case, it's √((-0.4)^2 + (0.9)^2) which equals 0.98.
What is the angle calculated at the end of the example problem, and what does it represent?
-The angle calculated is approximately 23 degrees, which represents the angle between the x-axis (east direction) and the resultant vector r.
What is the significance of breaking down vectors into components?
-Breaking down vectors into components allows for easier manipulation and calculation of resultant vectors, as well as providing a clear understanding of the vector's direction and magnitude.
How can one determine if a component of a vector is positive or negative?
-A component is positive if the vector moves in the direction of the axis (east for i_hat, north for j_hat), and negative if it moves in the opposite direction (west for i_hat, south for j_hat).
Outlines
📚 Vector Component Analysis
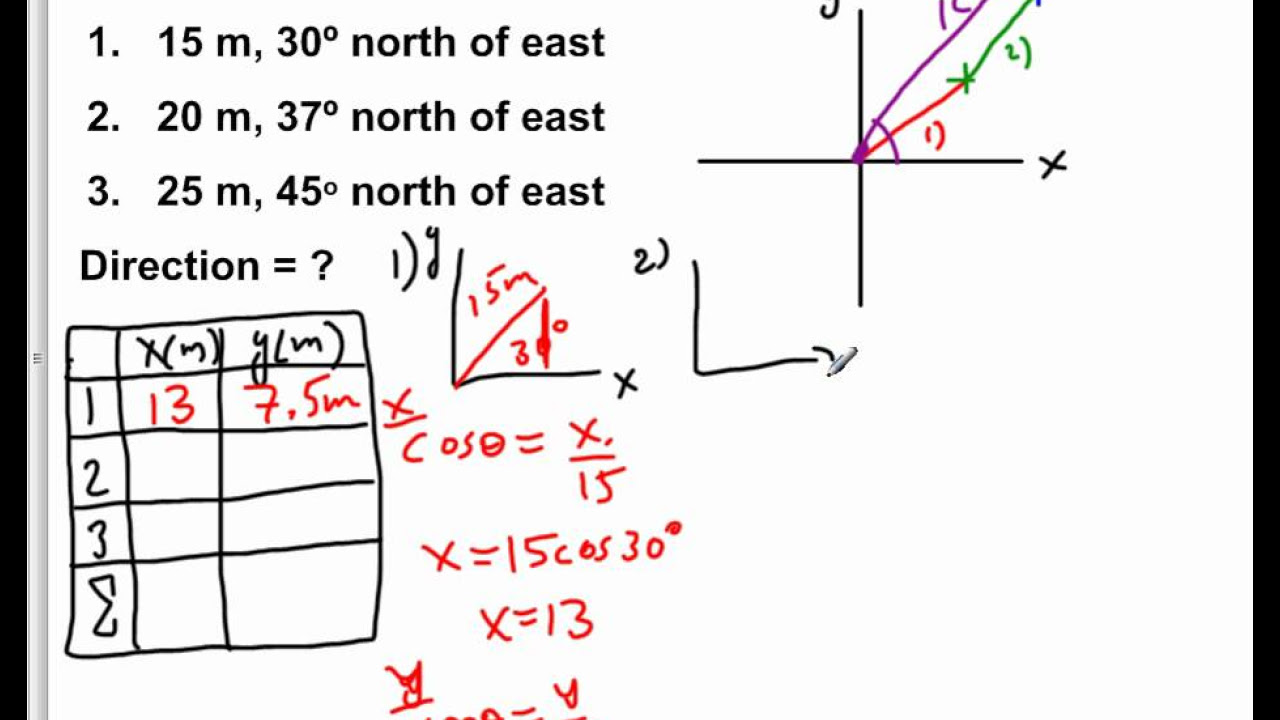
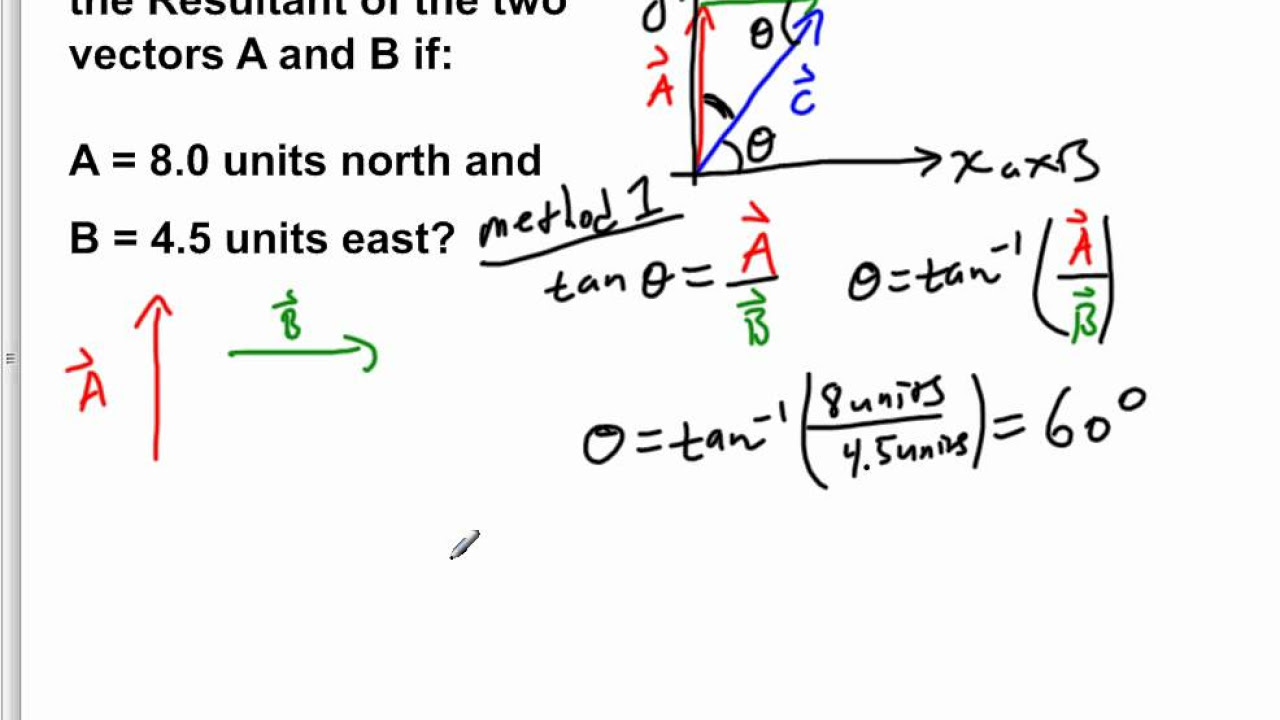
This paragraph introduces the concept of breaking down vectors into their components using unit vectors. The example problem revisits a journey involving traveling one mile north, 0.4 miles west, and 0.1 mile south. The goal is to determine the resultant vector (r) by identifying and summing up the individual vectors (a, b, and c) corresponding to each leg of the journey. Vector a is described as moving one mile in the j-hat direction (north), vector b as moving 0.4 miles in the negative x-direction (west), and vector c as moving 0.1 mile in the negative y-direction (south). The process of writing these vectors in component form is explained, emphasizing the use of i-hat and j-hat for the x and y directions, respectively.
🔢 Calculation of Resultant Vector and Angle
In this paragraph, the process of calculating the resultant vector is detailed. By summing up the components along the i and j axes, the resultant vector's components are found to be -0.4i and 0.9j. The magnitude of the resultant vector is calculated using the Pythagorean theorem, resulting in a value of 0.98. Furthermore, the angle between the resultant vector and the x-axis is determined using trigonometry, specifically the arc cosine function, yielding an angle of approximately 23 degrees. The explanation concludes with a review of the method and an invitation for further questions or clarification.
Mindmap
Keywords
💡Vector Components
💡Unit Vectors
💡Vector Addition
💡Magnitude of a Vector
💡Angle Calculation
💡Coordinate System
💡Direction
💡Displacement
💡Trigonometry
💡Pythagorean Theorem
💡Journey Legs
Highlights
Professor Anderson introduces a vector problem involving breaking down vectors into components.
The example problem revisits a journey with movements in different directions.
The first leg of the journey is one mile to the north.
The second leg involves moving 0.4 miles to the west.
The third leg is 0.1 miles to the south.
The goal is to determine the resultant vector r.
Vector a is represented as zero in the x-direction and one in the y-direction.
Vector b is represented with zero in the y-direction and negative 0.4 in the x-direction.
Vector c has no movement in the x-direction and negative 0.1 in the y-direction.
The resultant vector is found by adding the individual vectors' components.
The magnitude of the resultant vector r is calculated to be 0.98.
The angle of the resultant vector is determined to be 23 degrees using arc cosine.
The problem demonstrates the application of unit vectors in vector analysis.
The process involves clear labeling and understanding of vector components.
The method can be applied to solve real-world problems involving vector addition.
The lecture encourages students to approach vector problems methodically.
Professor Anderson invites questions and offers additional help for those who need it.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: