Vector Sum of Forces
TLDRIn this AP Physics essentials video, Mr. Andersen explores the concept of vector sum of forces, using demonstrations with a 1.0 kg mass and force meters to illustrate how forces split and combine at different angles. He explains the importance of considering both magnitude and direction when summing vectors, and introduces the use of free-body diagrams and Newton's second law to determine the overall force and acceleration of an object. The video also discusses practical applications such as using a force table and phet simulations to visually and mathematically calculate vector sums, emphasizing the relevance of these principles in understanding physical phenomena.
Takeaways
- 📌 The concept of vector sum is introduced, explaining how to calculate the overall force acting on an object when multiple forces are applied in different directions.
- 📈 A demonstration with a 1.0 kg mass and two force meters illustrates the difference between forces measured vertically and when forces are applied at a 90-degree angle, resulting in a vector sum of approximately 7.1 newtons.
- 🔍 The importance of maintaining the magnitude and direction of forces when performing a vector sum is emphasized, using the method of lining up forces tail to tip.
- 🛠️ Free-body diagrams are used to identify force vectors acting on an object, which can then be combined using vector sum to determine the object's acceleration according to Newton's second law.
- 🔧 A force table, a circular device with pulleys and a ring in the middle, is introduced as a tool for experimenting with force vectors and their vector sums.
- 🤖 The script describes using a force table to balance a 1.0 kg mass with three forces of 10 newtons each, resulting in a vector sum that can be visually observed.
- 📊 The use of a phet simulation is mentioned to demonstrate the vector sum of forces and its effect on the acceleration of an object.
- 🏗️ The script provides a practical example of a robot applying a force to a bucket, showing how the vector sum of forces affects the bucket's motion and how friction comes into play.
- 🧠 The problem-solving process using Newton's second law is outlined, where the net force (vector sum) is used to calculate the acceleration of an object with a given mass.
- 🧒 The script poses a problem involving a child being pushed by a robot, with given forces and friction, challenging the viewer to calculate the child's mass using the principles discussed.
- 📚 The video aims to teach viewers how to use a force table, create free-body diagrams, calculate vector sums, and apply Newton's second law to find the acceleration of objects.
Q & A
What is the concept of vector sum of forces discussed in the video?
-The vector sum of forces is the overall force acting on an object when multiple forces are applied in different directions. It is calculated by adding all the individual forces while maintaining their magnitude and direction, resulting in a single resultant force that can be used to determine the object's acceleration according to Newton's second law.
How does the weight of a 1.0 kilogram mass affect the force readings on two force meters in the vertical direction?
-The weight of a 1.0 kilogram mass, calculated by multiplying the mass by the gravitational field strength (9.8 m/s^2), results in a force of 9.8 newtons. When this force is split equally between two force meters in the vertical direction, each meter reads approximately 5 newtons.
What happens to the force readings when the force meters are separated by a 90-degree angle?
-When the force meters are separated by a 90-degree angle, the force readings are no longer 5 newtons each. Instead, they are approximately 7.1 newtons each due to the vector nature of the forces, which must be summed considering both magnitude and direction.
How is the vector sum of forces determined using a force table?
-A force table is a device used to visually determine the vector sum of forces. It consists of a circle with pulleys around the outside and a ring in the middle. By applying different forces to the ring using strings attached to the pulleys, the vector sum can be found by balancing the ring around a central peg, indicating the resultant force direction and magnitude.
What is the role of free-body diagrams in calculating the vector sum?
-Free-body diagrams are used to visually represent all the forces acting on an object. They help identify the force vectors, which can then be used to calculate the vector sum. This sum is essential for determining the overall acceleration of the object using Newton's second law.
How can the x and y components of forces be used to find the vector sum?
-By breaking down the individual forces into their x and y components, the vector sum can be determined by adding the components in each direction separately. The resultant x and y components are then used to find the magnitude and direction of the overall force acting on the object.
What is the significance of the vector sum in relation to Newton's second law?
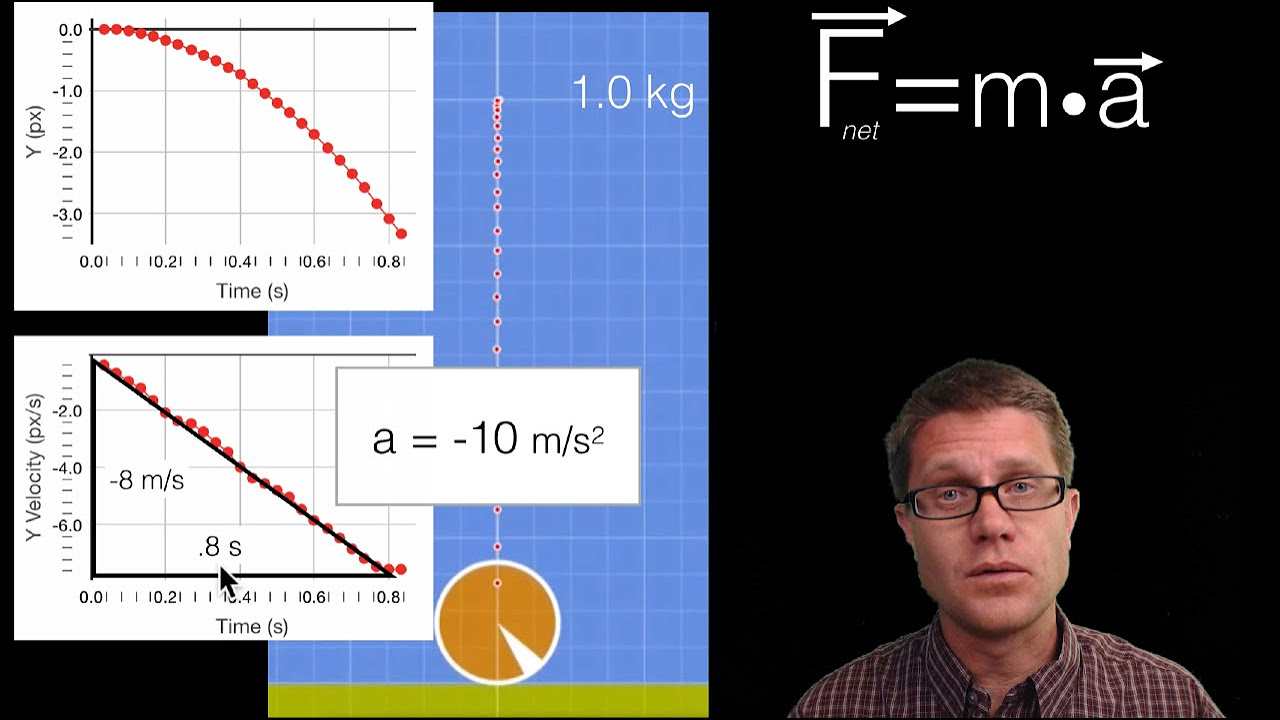
-The vector sum of forces is crucial in applying Newton's second law, which states that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. By finding the vector sum, one can calculate the net force and subsequently the acceleration of the object.
How does the simulation in the video demonstrate the effect of friction on the vector sum and acceleration?
-The simulation shows how the frictional force opposes the applied force, affecting the vector sum. When the applied force exceeds the frictional force, the object accelerates in the direction of the net force. Reducing friction allows the object to continue moving without a net force, demonstrating the balance between applied forces and friction.
What method is suggested in the video for determining the mass of an object using the vector sum and acceleration?
-By applying a known force and measuring the resulting acceleration, one can use Newton's second law (F = ma) to solve for the mass (m) of the object. The video provides an example where a 40 newton force results in an acceleration of approximately 9 m/s^2, allowing the viewer to calculate the mass of the child.
How does the video demonstrate the calculation of the vector sum using a phet simulation?
-The phet simulation allows the user to apply forces at specific angles and observe how these forces add up to form a vector sum. By adjusting the forces and angles, the simulation visually shows the resultant force vector, which can then be used to understand the overall force acting on an object.
What are some practical applications of understanding vector sums in physics experiments?
-Understanding vector sums is essential in various physics experiments and real-world applications, such as determining the stability of structures on inclined planes, analyzing the forces on moving objects, and designing mechanisms in engineering where accurate force balance is critical.
Outlines
📏 Introduction to Vector Sum of Forces
In this introductory segment, Mr. Andersen explains the concept of vector sum of forces using a practical demonstration involving a 1.0 kg mass and two force meters. The mass is subjected to gravitational force, calculated as 9.8 newtons, and the forces are split between the two scales. The discussion then moves to a scenario where the force meters are at a 90-degree angle, resulting in a different reading of approximately 7.1 newtons, highlighting the vector nature of forces when applied at different angles. The importance of understanding vector sum is emphasized, as it dictates the overall force and acceleration of an object according to Newton's second law. The use of free-body diagrams and force tables in physics labs to visualize and calculate vector sums is introduced.
🚀 Applying Newton's Second Law with Vector Sum
This section delves into applying Newton's second law to determine the acceleration of an object based on the vector sum of forces acting upon it. Mr. Andersen uses a simulation to demonstrate how the vector sum affects the motion of a bucket, with the frictional force balancing the applied force. The concept is further illustrated by reducing friction, leading to constant motion. A practical problem involving a robot pushing a box with specified forces and mass is used to calculate acceleration, reinforcing the application of Newton's second law. The segment concludes with a challenge problem where the viewer is prompted to estimate the mass of a child based on given forces and acceleration, with the answer provided in the video description.
Mindmap
Keywords
💡Vector Sum
💡Force Meters
💡Gravitational Field Strength
💡Newton's Second Law
💡Free-Body Diagrams
💡Frictional Force
💡Inclined Plane
💡Force Table
💡Phet Simulation
💡Acceleration
💡Mass
Highlights
Introduction to the concept of vector sum of forces and its application in physics.
Demonstration using a 1.0 kg mass and two force meters to explain the vertical force.
Explanation of how the force measured by the scales changes when the forces are applied at a 90-degree angle.
Discussion on the importance of considering direction when calculating the sum of vector forces.
Use of free-body diagrams to identify and analyze force vectors acting on an object.
Description of a force table and its use in the physics lab for practical understanding of force vectors.
Method of performing a vector sum by aligning force vectors from tail to tip.
Alternative approach to solving vector sum by breaking down forces into their x and y components.
Explanation of how to apply Newton's second law to determine the overall acceleration of an object.
Demonstration of the effect of friction on the vector sum and resulting acceleration through a simulation.
Problem-solving example involving a robot pushing a box with a net force and friction to calculate acceleration.
Application of Newton's second law to calculate the mass of an object given the net force and acceleration.
Engagement with the audience to solve a physics problem involving a child being pushed by a robot.
Encouragement for the audience to practice using a force table and free-body diagrams to understand vector sums.
Summary of the key concepts learned in the video: force tables, free-body diagrams, vector sums, and Newton's second law.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: