Newton's Second Law
TLDRIn this informative video, Mr. Andersen explores Newton's Second Law of Motion, F=ma, emphasizing its significance in AP Physics. He explains the concept of acceleration and how it relates to mass and force, using examples and simulations to illustrate the effects of constant force on objects of varying mass. The video also discusses the role of opposing forces like friction, and how they can nullify acceleration. Furthermore, Andersen clarifies the conditions for a system's acceleration and demonstrates how to calculate force and acceleration through real-world and simulated scenarios, ultimately highlighting the simplicity of applying Newton's second law to solve physics problems.
Takeaways
- 📝 Newton's Second Law is expressed as F=ma, representing the fundamental equation in AP Physics.
- 🔢 The net force (vector) is equal to mass times acceleration (also a vector), and they always align in direction.
- 🚀 Acceleration implies a change in velocity over time, with constant force leading to increasing speed.
- 🏋️ Mass influences acceleration; a larger mass results in slower acceleration under the same force.
- 🔄 System acceleration requires an external force; internal forces within a system do not cause system acceleration.
- 🌐 The center of mass velocity remains constant in a system unless acted upon by an external force.
- 📈 Mass and acceleration are inversely related; a smaller mass will accelerate more for the same force.
- 📊 Measuring acceleration can be done through simulations or physical methods like ticker tape timing.
- 📉 Negative acceleration indicates a downward change in velocity, as seen in the acceleration due to gravity.
- 🚀 Calculating force involves knowing mass and acceleration (F = ma), which can be applied to real-world scenarios like rocket motion.
- 📈 The position versus time graph shows a curved path during acceleration and a straight line during constant velocity.
Q & A
What is Newton's Second Law of Motion?
-Newton's Second Law of Motion states that the net force acting on an object is equal to the mass of the object multiplied by its acceleration (F=ma).
What does it mean for an object to accelerate?
-To accelerate means that an object's speed is increasing over time due to a constant force applied to it.
How does mass affect the acceleration of an object?
-The larger the mass of an object, the slower the acceleration will be for a given force, as acceleration is inversely proportional to mass.
What is the role of friction in the context of acceleration?
-Friction is a force that opposes motion. If there is a frictional force acting in the opposite direction to the applied force, it can prevent acceleration even if a force is being applied.
What must be true for a system to experience acceleration?
-For a system to experience acceleration, there must be a net force acting on it from an external object or source.
How can the relationship between force and acceleration be used to determine mass?
-If the force and acceleration are known, the mass can be calculated by rearranging the formula F=ma to m=F/a.
What method can be used to measure acceleration in a real-world scenario?
-Acceleration can be measured using video simulation or by marking a ticker tape at regular intervals and observing the changing distance between the marks over time.
How can the velocity and acceleration be determined from a position versus time graph?
-The slope of the position versus time graph indicates velocity. If the velocity is increasing, it implies acceleration. A constant increase in velocity over time indicates a constant acceleration.
What happens to the force and acceleration due to gravity when an object is taken to the moon?
-On the moon, the force due to gravity is approximately 1/6 of that on Earth. Consequently, the acceleration due to gravity would also be 1/6 of the acceleration on Earth.
How does Newton's Second Law help in solving problems involving force, mass, and acceleration?
-Newton's Second Law allows us to solve for any one of the three variables (force, mass, acceleration) if the other two are known, making it a powerful tool for solving physics problems.
What would be the acceleration graph of an object that is first accelerated and then allowed to coast?
-The acceleration graph would show a constant increase in acceleration while the force is applied, followed by a flat line at zero acceleration after the force is removed, indicating the object continues to move at a constant velocity.
Outlines
📚 Introduction to Newton's Second Law
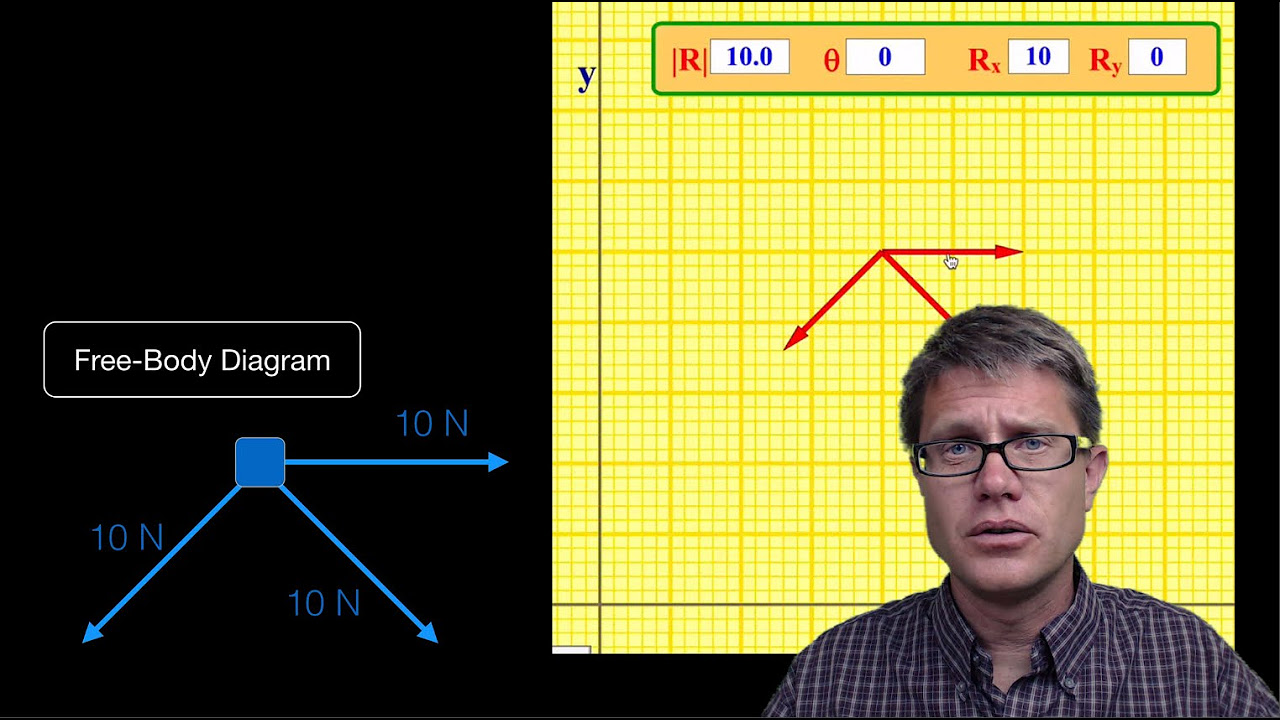
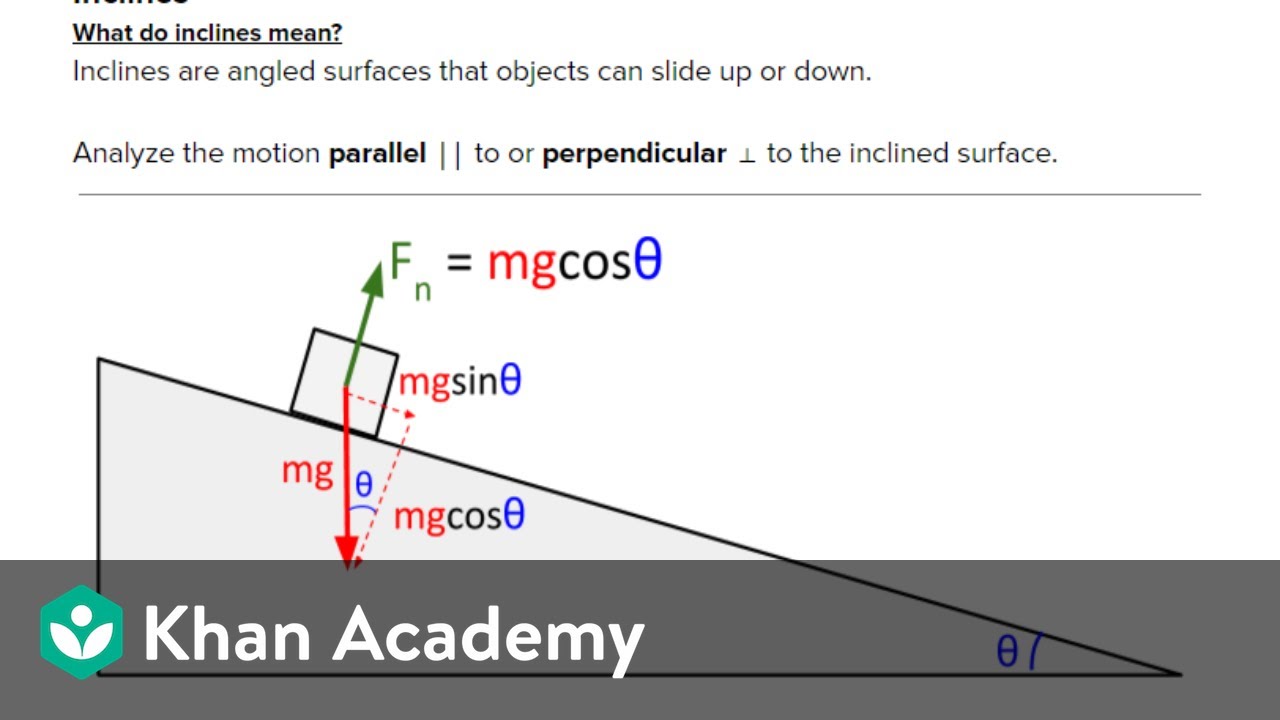
The video begins with Mr. Andersen introducing Newton's Second Law, often regarded as the most crucial equation in AP Physics, expressed as F=ma. He explains the concept of net force and its vector nature, emphasizing that force and acceleration are directionally aligned. Mr. Andersen then delves into the concept of acceleration, using the analogy of a large mass that, despite being pushed, does not accelerate due to opposing forces like friction. He illustrates the importance of net force for acceleration and the conditions under which a system accelerates, such as when an external force is applied. The segment also touches on the relationship between mass and acceleration within a system, using a simulation of two spheres to demonstrate how different masses respond to the same force, leading to different accelerations.
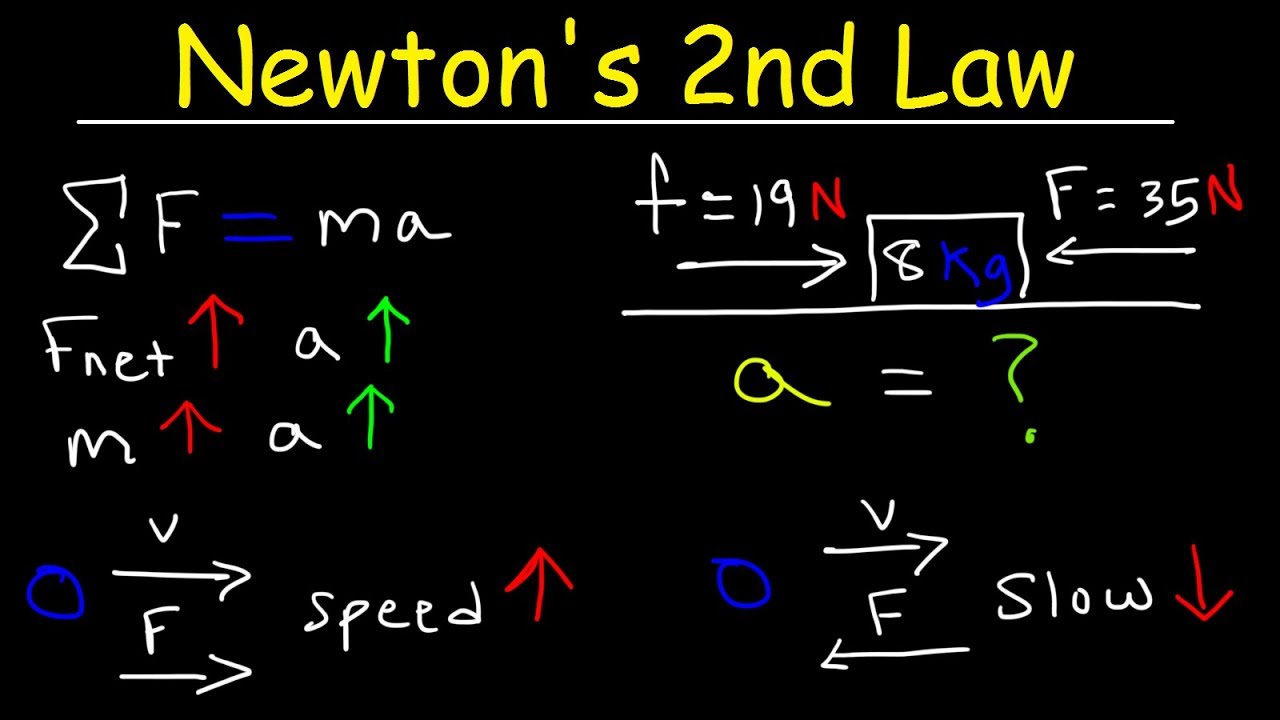
📈 Measuring and Applying Newton's Second Law
This paragraph focuses on the practical application and measurement of Newton's Second Law. Mr. Andersen explains how to calculate constant acceleration using the slope of a velocity vs. time graph, using a falling object as an example. He describes the process of marking positions at regular intervals to track acceleration and velocity changes. The video then connects the calculated acceleration to the force of gravity, illustrating how the force can be determined using mass and acceleration. The segment also discusses the effect of gravity on Earth versus the moon, showing how the force and resulting acceleration change with the gravitational constant. Mr. Andersen concludes by demonstrating how to plot position and velocity over time to understand the dynamics of an object under constant acceleration and when the net force is removed.
Mindmap
Keywords
💡Newton's Second Law
💡Vector
💡Frictional Force
💡Center of Mass
💡Acceleration
💡Mass
💡Net Force
💡Simulation
💡Velocity
💡Gravity
💡Force
Highlights
Newton's Second Law, F=ma, is introduced as the most important equation in AP Physics.
The net force is a vector and is equal to mass times acceleration, with both vectors being in the same direction.
Acceleration is described as the increase in speed over time due to a constant force.
Mass affects acceleration; larger mass results in slower acceleration under the same force.
Frictional forces oppose motion and can prevent acceleration even when a force is applied.
Removing opposing forces like friction allows for net force and subsequent acceleration.
A system with internal forces will not accelerate unless an external force is applied.
The center of mass velocity of a system does not change unless an external force acts on it.
Acceleration is a vector and is equivalent to the net force divided by mass.
The mass and acceleration of two objects are inversely related; greater acceleration implies a smaller mass when force is constant.
The force due to gravity (weight) is calculated using the mass and the acceleration due to gravity.
On the moon, the gravitational force is 1/6 of that on Earth, affecting the force and acceleration.
Newton's Second Law can be applied to solve problems involving force, mass, and acceleration.
The position versus time graph shows acceleration as increasing distance between marks over time.
The velocity versus time graph, derived from the position graph, indicates constant acceleration as a straight line.
The slope of the velocity versus time graph provides the constant acceleration value.
By knowing the mass and acceleration, one can calculate the net force using Newton's Second Law.
The position versus time graph of an object under constant force followed by coasting shows a transition from acceleration to constant velocity.
Visual representations, such as graphs, can be used to understand changes in the center of mass of a system.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: