Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (70 of 92) R=? T=? in terms of E & Vo

Michel van Biezen
29 Apr 201806:04
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, the focus is on calculating the transmission and reflection coefficients for a small particle encountering a potential step, where its energy exceeds the potential of the step. The explanation transitions from using wave numbers (K1 and K2) to expressing the coefficients in terms of particle energy (E) and the potential step (V_nought), which is more aligned with typical problem setups. The video simplifies the equations for both coefficients and emphasizes the relationship between them, noting that their sum must equal one. It sets the stage for practical examples in subsequent videos.

Takeaways
  • 📌 The discussion focuses on calculating transmission and reflection coefficients for a particle encountering a potential step.
  • 🔄 The coefficients are initially defined in terms of wave numbers K1 and K2, representing the particle's state before and after the potential step.
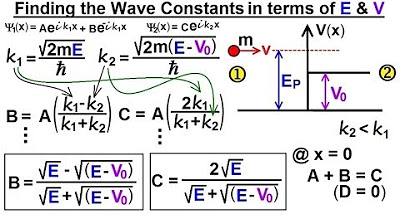
  • 💡 It's preferable to express T (transmission) and R (reflection) coefficients in terms of energies E and V_nought, as these are typically given in problems.
  • 🌟 The reflection coefficient R is derived from the wave numbers, with simplification showing cancellation of h-bar and the square root of 2m.
  • ✨ The transmission coefficient T is calculated using a similar approach, leading to a simplified formula involving energies and the potential step.
  • 🔢 Both coefficients are squared, reflecting the definition of these quantities in quantum mechanics.
  • 🎯 The simplified reflection coefficient formula is R = (sqrt(E - sqrt(E - V_nought)) / sqrt(E + sqrt(E - V_nought)))^2.
  • 🚀 The simplified transmission coefficient formula is T = 4 * sqrt(2m) * (sqrt(E) * sqrt(E - V_nought)) / ((2m) * (sqrt(E) + sqrt(E - V_nought)))^2.
  • ♻️ Once one coefficient is calculated, the other can be easily determined, since T + R must equal 1.
  • 📈 The process involves substituting given values for particle energy and potential step to find the coefficients.
  • 🔍 The script concludes by mentioning that examples will be provided in subsequent videos to illustrate the calculation process.
Q & A

  • What are the main topics discussed in the transcript?

    -The main topics discussed are the calculation of transmission and reflection coefficients for a small particle incident upon a potential step, where the energy of the particle is greater than the potential of the step.

  • What are the wave numbers K1 and K2 mentioned in the transcript?

    -K1 is the wave number of the particle on the left side before it reaches the potential step, and K2 is the wave number of the particle on the right side of the potential step.

  • How is the reflection coefficient initially expressed?

    -The reflection coefficient is initially expressed in terms of the wave numbers K1 and K2.

  • What is the significance of the energies E and V_sub_nought in the context of the problem?

    -E represents the energy of the particle and V_sub_nought represents the potential of the step. They are significant because the transmission and reflection coefficients are eventually expressed in terms of these energies, which are typically given in a problem.

  • How is the reflection coefficient simplified in terms of the particle's energy and the potential step?

    -The reflection coefficient is simplified by canceling out the h-bar (reduced Planck constant) in the numerator and denominator and dividing by the square root of two times the mass of the particle, resulting in an expression involving the square roots of the particle's energy and the difference between the particle's energy and the potential step.

  • What is the final form of the transmission coefficient equation?

    -The final form of the transmission coefficient equation is four times the square root of the product of 2m (mass of the particle), the square root of the energy difference, divided by the square root of the sum of the squares of the energy differences and the potential step difference.

  • How can you find the reflection coefficient if you have calculated the transmission coefficient?

    -If you have calculated the transmission coefficient, you can find the reflection coefficient by subtracting it from one, since the sum of the transmission and reflection coefficients must equal one.

  • Why is it important to verify the calculated coefficients?

    -Verification is important to ensure that the calculations are correct and to avoid mistakes, as the process involves complex mathematical expressions and the coefficients must sum up to one.

  • What will be shown in the next videos after the transcript?

    -The next videos will demonstrate examples of how to actually calculate the transmission and reflection coefficients.

  • What is the relationship between the potential step and the reflection and transmission of a particle?

    -The potential step acts as a barrier that can partially reflect and partially transmit the particle, depending on the energy of the particle relative to the potential of the step. The coefficients quantify these proportions.

  • How does the presence of a potential step affect the wave-like behavior of a particle?

    -The presence of a potential step disrupts the wave function of the particle, causing a portion of it to be reflected back and another portion to be transmitted through the step, altering its wave-like behavior.

Outlines
00:00
📚 Calculation of Transmission and Reflection Coefficients

This paragraph discusses the process of calculating the transmission and reflection coefficients for a small particle encountering a potential step, where the particle's energy exceeds the potential of the step. The explanation focuses on expressing T and R in terms of the particle's energy (E) and the potential step's potential (V_sub_nought), as these are typically the given parameters in such problems. The paragraph details the mathematical derivation of the reflection coefficient (R) and the transmission coefficient (T), emphasizing the simplification of the equations for practical use. It also introduces the concept that the sum of T and R must equal one, allowing for easy calculation of one from the other.

05:00
🔍 Verification and Simplification of Coefficient Calculations

The second paragraph emphasizes the ease of calculating the other coefficient (either transmission or reflection) once one has been determined, due to their sum being equal to one. It provides a methodological approach to verifying the accuracy of the calculated coefficients by calculating the other one using the relationship between them. The paragraph also highlights the potential for mistakes in the calculation process and suggests using the verification method to ensure the correctness of the results. It concludes by mentioning that future videos will provide examples to illustrate the calculation process.

Mindmap
Keywords
💡Transmission Coefficient (T)
The transmission coefficient, denoted as T, is a measure used in quantum mechanics to describe the probability of a particle passing through a potential barrier or step. In the context of the video, T is calculated using the energies of the particle and the potential step, and it represents the fraction of the particle's initial probability current that is transmitted through the step. The script provides a detailed mathematical formula for calculating T, emphasizing its dependency on the particle's energy (E) and the potential step's energy (V_sub_nought).
💡Reflection Coefficient (R)
The reflection coefficient, denoted as R, is another key concept in quantum mechanics that quantifies the probability of a particle being reflected by a potential barrier or step. In the video, R is calculated in a similar manner to T, but it represents the fraction of the particle's initial probability current that is reflected back from the step. The script provides a formula for R, highlighting its relationship with the particle's energy and the potential step's energy, and how it simplifies to a more manageable expression.
💡Potential Step
A potential step is a type of potential barrier in quantum mechanics that represents a sudden change in potential energy. It is characterized by a discontinuity at a certain point in space, often used to model scenarios where a particle encounters a change in the potential landscape. In the video, the potential step is the central scenario where the particle's interaction with the step leads to reflection and transmission phenomena, and the coefficients R and T are calculated to understand this interaction.
💡Wave Numbers (K1 and K2)
Wave numbers, denoted as K1 and K2 in the script, are quantities related to the wave-like behavior of particles in quantum mechanics. K1 represents the wave number of the particle on the left side of the potential step, while K2 is the wave number on the right side. These wave numbers are crucial in determining the reflection and transmission coefficients, as they are directly related to the particle's energy and the potential step's energy.
💡Energy (E)
In the context of the video, energy refers to the kinetic energy of the particle before it encounters the potential step. It is a fundamental quantity in quantum mechanics that determines the behavior of particles, including their transmission and reflection probabilities when encountering potential barriers. The energy of the particle is used in the formulas for calculating the transmission and reflection coefficients.
💡Potential Energy (V_sub_nought)
Potential energy, represented as V_sub_nought in the script, is the energy associated with the position of an object within a force field, such as a gravitational or electric field. In this case, it refers to the energy level of the potential step, which is the height of the energy barrier that the particle must overcome. The potential energy is a critical factor in determining the probabilities of reflection and transmission of the particle.
💡Quantum Mechanics
Quantum mechanics is a fundamental theory in physics that describes the behavior of matter and energy at very small scales, such as atomic and subatomic particles. It provides the framework for understanding phenomena like particle wave duality, quantum states, and quantum tunneling. The video's content is rooted in quantum mechanics principles, specifically focusing on the behavior of particles encountering potential steps.
💡Probability Current
In quantum mechanics, probability current is a measure of the flow of probability associated with a quantum state. It is used to describe the likelihood of finding a particle in a particular location over time. The transmission and reflection coefficients are directly related to the probability current, as they quantify the probability of a particle's wave function being transmitted or reflected at a potential step.
💡Schrödinger Equation
The Schrödinger Equation is a fundamental equation in quantum mechanics that describes how the quantum state of a physical system changes with time. It is used to determine the wave function of a system, which in turn can be used to calculate probabilities of various physical outcomes. While the Schrödinger Equation itself is not explicitly mentioned in the script, the concepts of transmission and reflection coefficients are derived from solutions to this equation.
💡h-bar (Reduced Planck Constant)
The reduced Planck constant, denoted as h-bar, is a fundamental constant in quantum mechanics that relates the energy of a photon to its frequency. It is equal to the Planck constant divided by 2π and has units of joule seconds (J*s). In the script, h-bar is used in the formulas for wave numbers and the transmission and reflection coefficients, indicating its importance in the quantization of energy and the behavior of particles at the quantum level.
💡Mass (m)
Mass, represented by the symbol m in the script, is a measure of the amount of matter in an object. In the context of quantum mechanics and the video, the mass of the particle is a crucial parameter that influences the wave numbers and the transmission and reflection coefficients. It is used in the calculations to determine the energy levels and the behavior of the particle when it interacts with the potential step.
Highlights

Calculation of transmission and reflection coefficients for a small particle incident upon a potential step.

The energy of the particle is greater than the potential of the potential step, leading to both reflection and transmission.

Initial expression of coefficients in terms of wave numbers K1 and K2, with K1 being the wave number to the left and K2 to the right of the potential step.

Desire to express T and R in terms of energies E and V_sub_nought for practical problem-solving.

Derivation of the reflection coefficient equation in terms of particle energy and potential step energy.

Simplification of the reflection coefficient by canceling out h-bar and the square root of 2m.

Derivation of the transmission coefficient equation using the initial wave number expressions.

Further simplification of the transmission coefficient by canceling out terms and factoring the energy difference.

The relationship that the sum of the transmission and reflection coefficients must equal one.

Efficiency in calculating coefficients by determining one and using the relationship to find the other.

Verification of calculated coefficients by ensuring they sum to one for accuracy.

Examples of calculating transmission and reflection coefficients will be provided in subsequent videos.

The importance of careful calculation to avoid mistakes in the derivation of coefficients.

The practical application of these calculations in understanding particle behavior at potential steps.

The use of mathematical simplification to make the equations more manageable for practical use.

The significance of the potential step's energy in determining the fate of the particle post-interaction.

The role of particle energy in the potential step scenario as a key factor in transmission and reflection.

Transcripts

Browse More Related Video

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (64 of 92) Transmission-Reflection (Q.M.)

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (67 of 92) Finding R=? T=? Coefficients

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (66 of 92) B=? C=? in terms of E & V0

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (71 of 92) R=? T=? V0=(1/4)E (Ex. 1 of 4)

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (72 of 92) R=? T=? V0=(1/4)E (Ex. 2 of 4)

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (83 of 92) Transmission Coeff=? (1 of 6)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Quantum MechanicsParticle PhysicsTransmission CoefficientReflection CoefficientPotential BarrierWave FunctionsEnergy StatesScientific CalculationElectron BehaviorPhysics Tutorial