Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (67 of 92) Finding R=? T=? Coefficients

Michel van Biezen
26 Apr 201808:22
EducationalLearning
32 Likes 10 Comments

TLDRThis lecture delves into the concepts of reflection and transmission coefficients, which describe the fraction of particles reflected or transmitted past a potential step. The reflection coefficient R is derived as the ratio of B^2 to A^2, while the transmission coefficient T is calculated as the square of the ratio of B to A, accounting for energy and wave number differences. The validity of these coefficients is confirmed by the fact that their sum equals one, reflecting the conservation of particles. The lecture also hints at future exploration of these coefficients in relation to particle energy and potential step characteristics.

Takeaways
  • 🌟 The reflection coefficient (R) is the fraction of particles reflected by a potential step, while the transmission coefficient (T) is the fraction transmitted past the step.
  • 🔢 R is calculated as the ratio of B^2 to A^2, where A and B are constants associated with the wave functions representing particles moving in opposite directions in region 1.
  • 📈 The probability of finding a particle in region 1 depends on the wave function squared, hence the B^2 term in the reflection coefficient formula.
  • 🌐 The transmission coefficient (T) is a ratio of the square of the constant in region 2 (C) to the constant in region 1 (A), considering the change in energy and wave number.
  • 🚀 The formula for T includes a compensation for the difference in wavelength, similar to the concept of refraction in light entering a different medium.
  • 🧮 The transmission coefficient can be expressed in terms of the energy of the particle and the potential of the step, which may be explored in a future video.
  • 🔍 To verify the correctness of the coefficients, it is checked that T + R equals 1, representing the conservation of particles (probability).
  • 🎯 The final expressions for R and T are derived after considering the wave numbers in regions 1 and 2, and the mathematical checks confirm their validity.
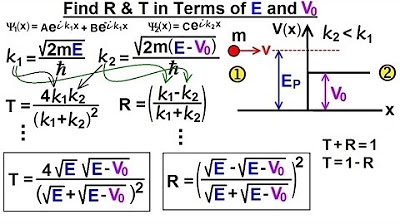
  • 📊 The reflection coefficient simplifies to a ratio of the difference in wave numbers between the two regions, (K1 - K2)^2 / (K1 + K2)^2.
  • 📈 The transmission coefficient simplifies to 4K2 / (K1 + K2)^2, after considering the energy and wave number differences.
  • 📝 The process of deriving these coefficients involves understanding the behavior of wave functions and their probabilities at a potential step.
Q & A

  • What are reflection and transmission coefficients?

    -Reflection coefficient R is the fraction or percentage of particles reflected off a potential step, while transmission coefficient T is the fraction or percentage of particles transmitted past the potential step.

  • How is the reflection coefficient calculated?

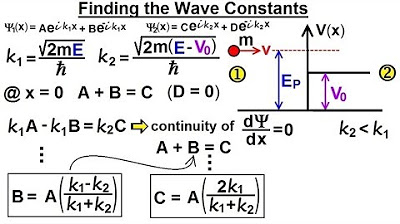
    -The reflection coefficient is calculated as the ratio of B squared to A squared, where B and A are constants in front of the terms representing particles moving in opposite directions in region 1.

  • Why is B squared used instead of B when calculating the reflection coefficient?

    -B squared is used because the probability of finding a particle in region 1 depends on the wave function squared, making it a ratio of probabilities, not wave functions.

  • What is the expression for the reflection coefficient in terms of wave numbers?

    -The reflection coefficient is given by the expression (K1 - K2) squared divided by (K1 + K2) squared.

  • How is the transmission coefficient related to the energy and potential of the step?

    -The transmission coefficient can be expressed in terms of the energy of the particle and the potential of the step by replacing K1 and K2 with their expressions related to energy and potential.

  • What consideration is necessary when calculating the transmission coefficient?

    -The difference in energy and wave number, or wavelength, between regions must be compensated for, similar to the concept of refraction in light entering a different medium.

  • What is the expression for the transmission coefficient?

    -The transmission coefficient is given by the expression 4K1K2 divided by (K1 + K2) squared.

  • Why are absolute value signs used in probability functions?

    -Absolute value signs are used because they represent the magnitude of the probability without regard to the direction of the wave function.

  • How can we verify the correctness of the expressions for R and T?

    -We can verify the expressions by checking if T plus R equals 1, as the sum of the fractions of particles transmitted and reflected must equal the total number of particles.

  • What does the result of adding the expressions for R and T indicate?

    -Adding the expressions for R and T and obtaining a result of 1 confirms that the expressions are correct, as it satisfies the condition that the total probability of particles being transmitted and reflected must equal 1.

  • How does the wavelength of a particle change when it enters a different region?

    -When a particle enters a different region, its wavelength may change, requiring compensation in the calculation of the transmission coefficient, similar to the change in wavelength when light enters a medium with a different refractive index.

Outlines
00:00
📚 Introduction to Reflection and Transmission Coefficients

This paragraph introduces the concepts of reflection and transmission coefficients, denoted as R and T respectively. These coefficients represent the fraction or percentage of particles reflected and transmitted past a potential step. The reflection coefficient R is explained as a ratio of B^2 to A^2, where B and A are constants related to the wave functions of particles in different regions. The transmission coefficient T is described as a ratio involving the constants of regions 1 and 2, taking into account the difference in energy and wave number, similar to the concept of refraction in optics. The paragraph concludes with a calculation of these coefficients in terms of the wave numbers of the regions.

05:00
🔍 Verification of the Derived Coefficients

The second paragraph focuses on verifying the correctness of the derived expressions for the reflection (R) and transmission (T) coefficients. It emphasizes the principle that the sum of R and T must equal 1, representing all particles either reflected or transmitted. The verification process involves algebraic manipulation of the expressions for R and T, ultimately showing that they add up to 1, confirming the accuracy of the derived formulas. This step ensures the integrity of the theoretical model and its applicability to physical scenarios.

Mindmap
Keywords
💡Reflection Coefficient (R)
The reflection coefficient (R) is a measure of the fraction or percentage of particles that are reflected off a potential step. In the context of the video, it is calculated as the ratio of B squared over A squared, where B represents the amplitude of particles moving to the left in region 1, and A represents all particles moving to the right in region 1. The reflection coefficient is crucial for understanding how particles interact with a potential barrier or step, as it indicates the probability of a particle being reflected back.
💡Transmission Coefficient (T)
The transmission coefficient (T) represents the fraction or percentage of particles that pass through a potential step. It is calculated as a ratio involving the constants in front of the wave functions for region 2 over those for region 1, taking into account the difference in energy and wave number between the two regions. This coefficient is essential for understanding the probability of a particle continuing its motion after encountering a potential barrier.
💡Potential Step
A potential step is a type of energy barrier that a particle may encounter in its path. It is characterized by an abrupt change in potential energy, which can cause the particle to be either reflected or transmitted. In the video, the potential step is used to illustrate the concepts of reflection and transmission coefficients, showing how particles interact with the step and the probabilities associated with their behavior.
💡Wave Function
A wave function is a mathematical description of the quantum state of a particle or system of particles. It provides information about the probability of finding a particle in a particular location or state. In the video, the square of the wave function is used to determine the probability of particles being in a certain region, which is crucial for calculating reflection and transmission coefficients.
💡Wave Numbers (K1 and K2)
Wave numbers (K1 and K2) are quantities related to the wave-like properties of particles in different regions. They are used to describe the energy and momentum of the particles. In the context of the video, K1 and K2 represent the wave numbers in regions 1 and 2, respectively, and are essential for calculating the reflection and transmission coefficients, as they reflect the difference in the particle's behavior when transitioning between regions with different potential energies.
💡Probability
In quantum mechanics, probability is a fundamental concept that describes the likelihood of a particle being found in a particular state or location. It is derived from the square of the wave function. The video emphasizes the importance of probability in calculating the reflection and transmission coefficients, which are essentially ratios of probabilities of particles being reflected or transmitted at a potential step.
💡Energy of the Particle
The energy of a particle is a measure of the work that it is capable of doing, often related to its motion or position in a potential field. In the video, the energy of the particle is crucial for determining the reflection and transmission coefficients, as it influences the wave numbers and the behavior of the particle when encountering a potential step.
💡Potential Energy
Potential energy is the stored energy an object has due to its position in a force field, such as a gravitational or electric field. In the context of the video, potential energy is associated with the step potential, which is the barrier that particles encounter. The potential energy of the step affects the wave numbers and thus the reflection and transmission coefficients, determining the particle's interaction with the potential step.
💡Refraction
Refraction is the change in direction and speed of a wave when it passes from one medium to another with a different refractive index. In the video, refraction is used as an analogy to explain the need to account for changes in wavelength and energy when particles move from one region to another with different potential energies.
💡Index of Refraction
The index of refraction is a measure of how much a substance slows down the speed of light compared to the speed of light in a vacuum. It is used to describe how light (or other electromagnetic radiation) changes direction when it enters a different medium. In the video, the index of refraction is mentioned as an analogy to explain the adjustment needed for the change in wavelength when particles move from one region to another with different potential energies.
💡Absolute Value
The absolute value of a number is its non-negative value, regardless of its sign. In the context of the video, absolute value is used in the transmission coefficient to ensure that the probability, which must be a positive quantity, is correctly represented. This is important because probabilities cannot be negative and are often expressed as absolute values in quantum mechanics.
Highlights

The reflection coefficient (R) is the fraction of particles reflected at a potential step.

The transmission coefficient (T) is the fraction of particles transmitted past a potential step.

Reflection coefficient is calculated as the ratio of B^2 to A^2, representing probabilities of particles in different regions.

B^2 over A^2 is used because the probability depends on the wave function squared.

The transmission coefficient is a ratio of the square of the constant in region 2 to the constant in region 1.

Compensation for different energy and wave number is necessary, similar to refraction in optics.

The transmission coefficient is given by the expression 4K1K2 / (K1 + K2)^2.

T plus R must equal 1, representing all particles either reflected or transmitted.

The mathematical check confirms that the sum of the transmission and reflection coefficients equals 1.

The difference in wave numbers in region 1 and region 2 is crucial for determining the reflection coefficient.

The wave function's square root is considered when calculating the transmission coefficient.

The reflection and transmission coefficients are derived in terms of the energy of the particle and the potential step.

The process of finding the coefficients involves a detailed understanding of quantum mechanics and wave functions.

The lecture provides a comprehensive explanation of how to calculate quantum mechanical coefficients.

The mathematical derivation is based on the principles of quantum mechanics and the behavior of particles at a potential step.

The lecture is a part of a series that delves into the quantum mechanical analysis of particles at potential steps.

The explanation includes the use of wave numbers and their relationship with energy and potential.

The lecture is aimed at individuals with a background in physics or a related field, as it requires an understanding of complex quantum concepts.

Transcripts

Browse More Related Video

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (71 of 92) R=? T=? V0=(1/4)E (Ex. 1 of 4)

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (64 of 92) Transmission-Reflection (Q.M.)

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (70 of 92) R=? T=? in terms of E & Vo

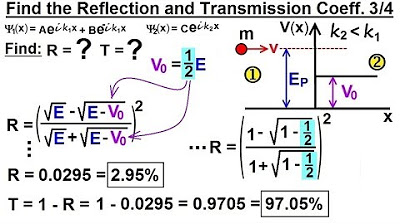
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (73 of 92) R=? T=? V0=(1/2)E (Ex. 3 of 4)

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (65 of 92) Wave Constants B=? C=?

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (74 of 92) R=? T=? V0=(3/4)E,.(Ex. 4 of 4)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
QuantumMechanicsParticlePhysicsPotentialBarriersWaveFunctionsProbabilityCalculationsPhysicsEducationLectureSeriesTechnicalExplanationEducationalContentScienceCommunication