Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (66 of 92) B=? C=? in terms of E & V0

Michel van Biezen
25 Apr 201804:09
EducationalLearning
32 Likes 10 Comments

TLDRIn this lecture, the speaker demonstrates how to express wave equations in terms of particle energy and barrier potential, rather than wave numbers. By replacing K1 and K2 with energy-based expressions, the equations are simplified through the elimination of h-bar and the square root of 2m. The process results in new wave functions with a single constant 'a', where B and C coefficients are determined by the energy of the particle and the potential difference. This approach provides a clearer understanding of quantum mechanics and barrier penetration.

Takeaways
  • 📚 The lecture focuses on expressing wave equations using the energy of a particle and the potential energy of a barrier rather than wave numbers.
  • 🔄 The wave numbers K1 and K2 are replaced with expressions involving the energy of the particle (E) and the potential of the barrier (V).
  • 🌟 The constant B is derived by using the square root of (2mE/h-bar) minus K2, which includes the potential energy difference.
  • 📈 The terms in the derived expressions have h-bar in the denominator, which can be canceled out for simplification.
  • 🔢 The radical in the expressions contains a factor of 2m, allowing for the simplification by dividing both numerator and denominator by the square root of 2m.
  • 🔄 The constant C is also expressed in terms of the energy of the particle and the potential of the barrier, mirroring the process for B.
  • 🌐 The final expressions for B and C are simplified to include only one constant, 'a', and are related to the energy of the particle and the potential of the barrier.
  • 📑 The new set of functions or wave functions obtained from B and C can be substituted into the original equations to solve for the wave behavior.
  • 🔑 The values of B and C are dependent on the energy of the particle and the potential of the barrier, which is crucial for solving the wave equations.
  • 🚦 The process demonstrated in the lecture is a method to simplify quantum mechanical problems involving potential barriers and particle energies.
Q & A

  • Why is it beneficial to express the constants in terms of energy rather than wave numbers?

    -Expressing the constants in terms of energy rather than wave numbers allows for a more intuitive understanding of the wave equations, as it directly relates to the physical quantities of the particle and the potential barrier, making the mathematical expressions more meaningful in a physical context.

  • What are the two main regions mentioned in the script?

    -The two main regions mentioned in the script are Region 1 and Region 2, which are used to differentiate between different areas in the context of wave equations and their associated wave numbers (K1 and K2).

  • How is the wave number K1 related to the energy of the particle?

    -The wave number K1 is related to the energy of the particle through the expression B, which is equal to the square root of (2 times the mass of the particle times the energy of the particle divided by h-bar) minus K2.

  • What is the significance of h-bar in the wave equations?

    -H-bar, or reduced Planck's constant, appears in the denominator of the expressions for B and C, indicating its fundamental role in quantum mechanics. It is used to ensure that the energy values are properly scaled when converting between wave numbers and energy levels.

  • How does the potential of the barrier affect the wave equations?

    -The potential of the barrier is subtracted from the energy of the particle in the expressions for B and C, indicating that it influences the probability and behavior of the particle's wave function. The difference in energy between the particle and the barrier is crucial for determining the transmission and reflection coefficients.

  • What is the role of the constant 'a' in the simplified expressions?

    -The constant 'a' appears in the numerator of the expressions for B and C after simplification, representing a factor that scales the energy differences in the equations. It is crucial for determining the coefficients that describe the wave functions across the potential barrier.

  • How are the expressions for B and C related to each other?

    -Both B and C are derived from the original wave equations and are related through their dependence on the energy of the particle and the potential of the barrier. They are used to find the wave functions that describe the particle's behavior when encountering a potential barrier.

  • What happens to the terms with h-bar when simplifying the expressions?

    -When simplifying the expressions, all terms containing h-bar cancel out because they appear in both the numerator and the denominator, resulting in simplified expressions that are easier to work with.

  • How do the expressions for B and C change when considering the potential barrier?

    -The expressions for B and C incorporate the potential of the barrier by including terms that represent the difference between the energy of the particle and the potential of the barrier. This difference affects the transmission and reflection of the particle's wave function at the barrier.

  • What is the significance of the square root of 2m in the expressions for B and C?

    -The square root of 2m is a factor that relates to the mass of the particle and is part of the expressions for B and C. It is involved in the calculation of the wave numbers and the coefficients that describe the wave functions in the presence of a potential barrier.

  • How do the values of B and C influence the wave functions?

    -The values of B and C are coefficients that determine the shape and behavior of the wave functions. They depend on the energy of the particle and the potential of the barrier, and by substituting these values into the wave equations, one can obtain the new set of functions that describe the particle's wave behavior across the barrier.

Outlines
00:00
📚 Quantum Mechanics: Wave Equations and Energy

This paragraph introduces a method for expressing wave equations in terms of particle energy and barrier potential, rather than wave numbers. The speaker explains the process of replacing K1 and K2 with energy-related expressions, leading to a simplified equation. The explanation includes the mathematical manipulation of terms involving the mass of the particle, energy, and the potential barrier, ultimately resulting in a new set of wavefunctions with a single constant 'a'. The process is also applied to find the coefficients B and C, which depend on the energy of the particle and the potential of the barrier.

Mindmap
Keywords
💡Lecture
A lecture is an educational presentation where an expert or instructor imparts knowledge or information to a group of individuals. In the context of the video, the lecture is being delivered online and focuses on a specific topic in physics, involving wave equations and quantum mechanics.
💡Constants
In mathematics and physics, constants are values that do not change. They are often used in equations to represent fundamental properties or quantities. In the video, the constants are related to the wave equations and the energy of a particle and the potential barrier.
💡Wave Equations
Wave equations are mathematical models that describe the behavior of waves as they propagate through space. They are fundamental in physics, particularly in the study of quantum mechanics and wave-particle duality. The video discusses modifying the standard form of these equations to better understand particle behavior in the presence of a potential barrier.
💡Energy
Energy is a fundamental concept in physics that describes the capacity to do work or the cause of motion. In the context of the video, energy is used to describe the state of a particle, and it is a key factor in determining the wave functions and behavior in the presence of a barrier.
💡Particle
In physics, a particle is an object whose size and shape can be ignored in the context of the problem being studied, allowing it to be treated as a point mass. The video focuses on the energy of a particle and its interaction with a potential barrier.
💡Barrier
A barrier in the context of physics, particularly quantum mechanics, is a region of space where a particle has a lower probability of being found due to an increase in potential energy. The video discusses the potential of the barrier and its role in the wave equations.
💡Potential
In physics, potential refers to the possibility or capacity for change in energy. It is often used to describe the energy state of a system or object in a particular configuration. In the video, the potential is related to the barrier and the energy of the particle.
💡H-bar
H-bar, or h-bar, is a constant used in quantum mechanics, representing the reduced Planck constant. It is a fundamental constant that relates the energy of a photon to its frequency. In the video, h-bar is used in the expressions for wave numbers and energy-related equations.
💡Wave Numbers
Wave numbers are quantities used in wave physics to describe the spatial frequency of a wave. They are inversely proportional to the wavelength. In the video, wave numbers are initially used in the wave equations but are later replaced by energy-related expressions.
💡Simplification
Simplification in mathematics refers to the process of making a complex expression or equation easier to understand or solve by reducing it to a simpler form. In the video, simplification is used to make the wave equations more manageable and directly related to the energy concepts.
💡Functions
In mathematics, functions are relations that define a unique output for each input. In physics, functions can describe the behavior of physical systems. The video discusses wave functions, which are mathematical descriptions of wave-like phenomena, such as the behavior of particles in the presence of a potential barrier.
Highlights

The lecture introduces a method to express wave equations in terms of particle energy and barrier potential rather than wave numbers.

The wave equations are reformulated to relate the constants K1 and K2 to the energy of the particle and the potential of the barrier.

The constant B is derived with a new expression involving the square root of 2 times the mass of the particle times the energy of the particle divided by h-bar minus K2.

The simplification of the expression for B involves canceling out common terms such as h-bar and the square root of 2m.

The constant C is also redefined using the energy of the particle and the potential of the barrier, with a focus on the cancellation of h-bar and the square root of 2m.

The new expressions for B and C allow for the creation of a new set of wave functions with only one constant, a.

The values of B and C will depend on the energy of the particle and the potential of the barrier, which is a practical approach for solving wave functions in quantum mechanics.

The lecture demonstrates the process of replacing wave numbers with energy terms to simplify quantum mechanical calculations.

The method presented can be applied to different regions and barriers, providing a versatile approach to quantum wave function analysis.

The process of simplifying the wave equations involves recognizing and canceling out common factors in the numerator and denominator.

The lecture emphasizes the importance of not forgetting the constant a in the derived expressions for B and C.

The approach taken in the lecture can lead to a better understanding of quantum behavior and potential energy barriers.

The lecture provides a step-by-step guide on how to transform wave equations to focus on energy rather than wave numbers.

The mathematical manipulations shown in the lecture are crucial for solving quantum mechanical problems involving potential barriers.

The lecture's method offers a clear and concise way to express complex quantum mechanical concepts in a more understandable form.

The process of simplifying the expressions for B and C illustrates the power of algebraic manipulation in quantum mechanics.

The lecture's content is an example of the practical application of quantum mechanics principles in solving physical problems.

Transcripts

Browse More Related Video

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (64 of 92) Transmission-Reflection (Q.M.)

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (52 of 92) A Closer Look at the Equation

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (75 of 92) Penetration Depth V0, E

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (76 of 92) Penetration Depth V0, E: Ex.

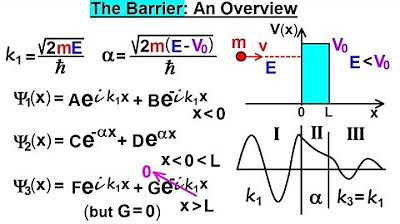
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (77 of 92) The Barrier: An Overview

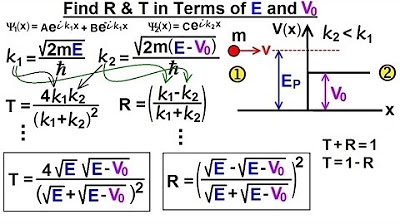
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (70 of 92) R=? T=? in terms of E & Vo

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
QuantumMechanicsWaveEquationsEnergyAnalysisMathLectureParticleEnergyBarrierPotentialSimplificationOnlineLearningPhysicsEducationQuantumBarrier