Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (83 of 92) Transmission Coeff=? (1 of 6)

Michel van Biezen
12 May 201804:01
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the process of calculating the transmission coefficient, a measure of the probability of a particle passing through a barrier in quantum mechanics. It outlines the method of setting up boundary conditions and solving a system of equations to find the relationship between the amplitudes of waves in different regions. The process involves equating wave functions and their derivatives at the boundaries and solving for constants, leading to the determination of the transmission coefficient. The script sets the stage for a step-by-step guide, promising further explanation in subsequent videos.

Takeaways
  • 📌 The transmission coefficient is used to calculate the probability of a particle passing through a barrier.
  • 🔍 To apply the transmission coefficient, boundary conditions at both sides of the barrier must be identified.
  • 🌐 The wave function of region one is set equal to the wave function of region two, and their derivatives are also set equal.
  • 🔄 Similarly, the wave function and its derivative of region two are set equal to those of region three.
  • 📈 This process results in four equations with five unknowns (a, b, c, d, and F), which allows for the solution of the transmission coefficient.
  • 🚫 Since there's no reflection in region three, constants B and F are set to zero.
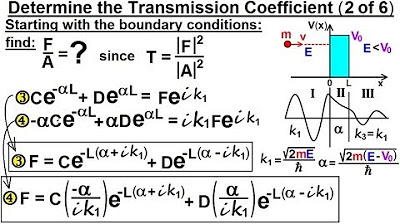
  • 📌 By solving the first equation for B and substituting it into the second, we eliminate B and simplify the system.
  • 📊 The wave number in region 1 (K1) and the exponential decay constant in region 2 (alpha) are crucial for the calculations.
  • 🔢 The equation is further simplified by dividing terms and rearranging to express 'a' in terms of C and D.
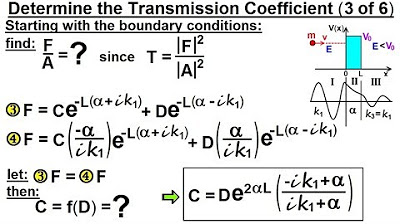
  • 🔍 The next step involves solving the remaining equations for F and setting them equal to each other to find the fraction F/a.
  • 🎥 The detailed algebraic process is carried over to the next video, promising a step-by-step guide on how to proceed.
Q & A

  • What is the main purpose of using the transmission coefficient in quantum mechanics?

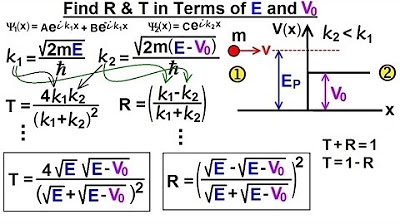
    -The transmission coefficient is used to calculate the probability of a particle passing through a potential barrier, despite the potential being higher than the particle's energy.

  • What boundary conditions are necessary to solve for the transmission coefficient?

    -The boundary conditions involve setting the wave function at the two sides of the barrier equal to each other and ensuring their derivatives are also equal at the interfaces of different regions.

  • How many equations are derived from the boundary conditions in the example given?

    -Four equations are derived from the boundary conditions, one for each interface between regions one and two, and regions two and three.

  • What constants are involved in the equations to find the transmission coefficient?

    -The constants involved are a, b, c, d, and F. Constants B and G are set to zero because there is no reflection in region three.

  • Why are B and G set to zero in the equations?

    -B and G are set to zero because there are no particles moving to the left in region three to cause reflection, hence no incoming wave in that region.

  • What does the wave number K1 represent in the context of the script?

    -The wave number K1 represents the wave number in both region 1 and region 3, which is used in the equations to describe the behavior of the wave function.

  • What is the significance of the exponential decay constant alpha in region 2?

    -The exponential decay constant alpha represents the rate at which the wave function decays in region 2, where the potential is higher than the particle's energy, leading to an exponential decay of the wave function.

  • How is the constant B eliminated from the equations?

    -B is eliminated by solving the first equation for B, expressing it as C plus D minus a, and then substituting this expression into the second equation, effectively removing B from the remaining equations.

  • What is the process to express the constant a in terms of C and D?

    -By dividing both sides of the equation derived from the boundary conditions by 2 i K1 and rearranging the terms, a is expressed in terms of C and D, which helps in eliminating B and further solving for the transmission coefficient.

  • What is the next step after eliminating B from the equations?

    -The next step is to solve the next two equations (equations 3 and 4) for F, setting them equal to each other, which will eventually lead to finding the fraction F over a.

  • How does the process of solving for the transmission coefficient involve the constants C and D?

    -After eliminating B, the equation is rearranged to express a in terms of C and D. Further steps involve solving for F in terms of these constants, which is necessary to calculate the transmission coefficient as F/a.

Outlines
00:00
🌟 Quantum Mechanics: Solving for Transmission Coefficient

This paragraph introduces the process of calculating the transmission coefficient in quantum mechanics. It explains the need to find boundary conditions at both sides of a barrier and how to set up the wave function and its derivative to be equal across regions. The paragraph details the algebraic steps involved in solving the resulting system of equations to find the fraction F over a, which represents the amplitude of the wave in region three and is related to the transmission coefficient. This coefficient is used to determine the probability of a particle passing through a barrier. The explanation includes the introduction of constants a, B, C, D, and F, and the algebraic manipulation required to eliminate unknowns and solve for the transmission coefficient, which will be continued in the next video.

Mindmap
Keywords
💡Transmission Coefficient
The transmission coefficient is a measure used in quantum mechanics to describe the probability of a particle passing through a potential barrier. In the context of the video, it is calculated by solving a set of equations that relate the wave functions and their derivatives at the boundaries of different regions. The coefficient is derived from the ratio of the amplitude of the wave in region three to that in region one, squared, representing the likelihood of a particle making it through the barrier.
💡Boundary Conditions
Boundary conditions are the constraints applied to the solutions of differential equations at the edges of the problem domain. In the video, they are used to connect the wave functions and their derivatives at the two sides of the barrier, ensuring a continuous and physically meaningful solution for the particle's behavior. These conditions are essential for calculating the transmission coefficient.
💡Wave Function
A wave function is a mathematical description in quantum mechanics that provides information about the probability amplitude of a particle's location. It is a fundamental concept used to calculate the transmission coefficient, as it describes the behavior of a particle in different regions and how it changes when encountering a barrier.
💡Quantum Mechanics
Quantum mechanics is a fundamental theory in physics that describes the behavior of matter and energy at the atomic and subatomic scales. The principles of quantum mechanics are applied in the video to explain the transmission of particles through potential barriers, as represented by the calculation of the transmission coefficient.
💡Potential Barrier
A potential barrier is a region in space where the potential energy is higher than the energy of a moving particle. In quantum mechanics, it is possible for particles to pass through such barriers, a phenomenon known as quantum tunneling. The video discusses calculating the probability of this occurrence using the transmission coefficient.
💡Amplitude
Amplitude in the context of waves refers to the maximum displacement of particles from their equilibrium position. In quantum mechanics, it relates to the probability of finding a particle in a particular location. The amplitude of the wave function in different regions is used to calculate the transmission coefficient.
💡Algebraic Challenge
An algebraic challenge refers to a complex problem in algebra that requires solving a system of equations or manipulating expressions to find a solution. In the video, the algebraic challenge is solving the set of equations that describe the boundary conditions to find the transmission coefficient.
💡Constants
In mathematics and physics, constants are values that do not change and are used to define the parameters of equations or models. In the context of the video, constants like a, B, C, D, and F are used to represent the amplitudes and other fixed values in the equations that describe the wave function across different regions.
💡Exponential Decay
Exponential decay is a mathematical model that describes a quantity approaching zero at a rate proportional to its current value. In the context of the video, it refers to the decrease in the wave function's amplitude as a particle moves through a potential barrier where the barrier's potential exceeds the particle's energy.
💡Solving Equations
Solving equations involves finding the values of unknowns that make the equations true. In the video, solving equations is the process of determining the constants that relate the wave functions at the boundaries of the potential barrier, which is necessary to calculate the transmission coefficient.
💡Probability
In the context of quantum mechanics, probability refers to the likelihood of a particle being found in a particular state or location. The transmission coefficient calculated in the video is directly related to the probability of a particle passing through a potential barrier.
Highlights

Exploring the transmission coefficient in quantum mechanics.

Setting up boundary conditions for a particle passing through a barrier.

Equating the wave function of region one to region two and their derivatives.

Similarly, equating the wave function and derivatives of region two to region three.

Deriving four equations from the boundary conditions to find the transmission coefficient.

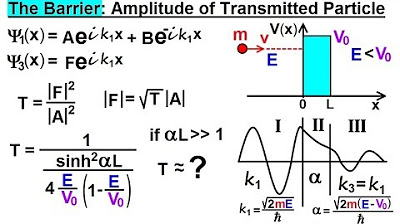
The transmission coefficient relates the amplitude of the wave in region three to that in region one.

Squaring the ratio of F to a gives the transmission coefficient, which is related to the probability of a particle passing through the barrier.

The algebraic challenge of solving for the transmission coefficient is addressed step by step.

Constants a, b, c, and d are introduced, with F and G initially set to zero.

Elimination of constant B by solving the first equation for B.

Substituting B into the second equation to eliminate it and simplify the expression.

Resulting equation with terms involving the wave number in region 1 (K1) and the exponential decay constant (alpha) in region 2.

Further simplification leads to expressing 'a' in terms of C and D.

The next step involves solving the third and fourth equations for F to find the ratio F/a.

Equations 3 and 4 are solved simultaneously to find the fraction F/a, which is essential for the transmission coefficient.

The process requires additional work and will be continued in the next video.

The method described is crucial for understanding quantum tunneling and its applications.

Transcripts

Browse More Related Video

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (84 of 92) Transmission Coeff=? (2 of 6)

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (85 of 92) Transmission Coeff=? (3 of 6)

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (78 of 92) The Barrier: Amplitude

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (64 of 92) Transmission-Reflection (Q.M.)

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (70 of 92) R=? T=? in terms of E & Vo

How to Solve Constant Coefficient Homogeneous Differential Equations

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
QuantumMechanicsTransmissionCoefficientParticleBarrierWaveFunctionAlgebraicSolutionProbabilityCalculationPhysicsEducationElectronBehaviorBarrierDecayQuantumTunneling