Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (64 of 92) Transmission-Reflection (Q.M.)

Michel van Biezen
22 Apr 201805:13
EducationalLearning
32 Likes 10 Comments

TLDRThe lecture delves into quantum mechanics, focusing on wave equations and their implications at boundaries, particularly when a particle's energy exceeds a barrier's potential. It explains how particles can be found on either side of the boundary, with the wave function's behavior and the reflection and transmission of particles. The relationship between wave numbers (k1 and k2) and the energy of particles on both sides of the barrier is discussed, along with boundary conditions that determine the coefficients for transmitted and reflected waves. The lecture emphasizes the importance of understanding these concepts to grasp quantum mechanical phenomena.

Takeaways
  • 🌊 The lecture focuses on quantum mechanics, specifically at the boundary where a particle's energy is greater than the potential barrier.
  • 📝 The wave equation is central to understanding the behavior of particles at such boundaries, with its second derivative equal to -k1^2 times the wave function.
  • 🔢 k1 is defined as the square root of 2m times E/h-bar, representing the wave number when the particle's energy is greater than the barrier's potential.
  • 🌟 Once the particle crosses the barrier, its total energy decreases, leading to a modified wave equation with -k2^2, where k2 is smaller than k1 due to the energy loss.
  • 💡 The general solution to the wave equation is expressed with different coefficients and wave numbers on either side of the barrier.
  • 🚦 At the boundary, particles can be reflected or transmitted, with the wave function being a sinusoidal wave moving to the right or left.
  • 🔄 The boundary conditions at x=0 require that the sum of the particles moving to the right equals the sum of those moving to the left plus those transmitted across the boundary.
  • 📉 If k2 equals 0, it means the particle's energy is equal to the potential of the barrier, and no particles are transmitted; all are reflected.
  • 🔼 When the particle's energy is greater than the barrier's potential (k2 > 0), some particles are transmitted and some are reflected.
  • 🧠 Understanding the wave equations, boundary conditions, and the meaning of variables and constants is crucial for grasping quantum mechanical phenomena at boundaries.
Q & A

  • What is the main topic of the lecture?

    -The main topic of the lecture is the behavior of particles at the boundary in the quantum mechanical world, specifically when the energy of the particle is greater than the potential of the barrier.

  • What is the wave equation discussed in the lecture?

    -The wave equation discussed is a differential equation where the second derivative of the wave function is equal to minus k1 squared times the wave function, with k1 defined as the square root of 2m times E divided by h-bar.

  • How does the potential barrier affect the energy of a particle?

    -When a particle encounters a potential barrier, some of its energy is taken up by the barrier, resulting in the particle having less total energy on the other side of the barrier.

  • What are the two possible scenarios for a particle at the boundary?

    -The two possible scenarios are that the particle can be on the left side of the boundary or on the right side of the boundary.

  • How are the wave functions described on either side of the barrier?

    -On the left side of the barrier, the wave function is a sinusoidal wave moving to the right and left, represented by a times e to the ikx and b times e to the minus ikx. On the right side, the wave function has different coefficients C and D and a different wave number k2 due to the reduced energy.

  • What happens at the boundary when no particles are moving to the left?

    -When no particles are moving to the left, the coefficient D must be zero, and the general solution simplifies to only include the transmitted particles on the right side of the barrier.

  • How are the boundary conditions applied in this scenario?

    -The boundary conditions are applied by equating the wave function and its derivative at the boundary (x=0) to ensure continuity and physical relevance.

  • What is the significance of the K factor in the context of this lecture?

    -The K factor represents the energy of the particles on both sides of the boundary and is crucial in determining the number of particles transmitted and reflected.

  • What happens when the energy of the particle is equal to the potential of the barrier?

    -When the energy of the particle is equal to the potential of the barrier, no particles are transmitted, and all particles reaching the boundary are reflected.

  • What is the conclusion of the lecture regarding particles with energy greater than the barrier potential?

    -The conclusion is that when the energy of the particles is greater than the potential of the barrier, some particles are transmitted and some are reflected, with the exact number depending on the relative energies and wave numbers on either side of the barrier.

Outlines
00:00
🌐 Quantum Mechanics: Wave Equation at Boundaries

This paragraph delves into the quantum mechanical concept of wave equations at boundaries, particularly when a particle's energy exceeds the potential barrier. It introduces the differential equation that governs the wave function, highlighting the role of the wave number (k1) and how it changes after crossing the barrier (k2). The discussion includes the general solution for the wave function on either side of the barrier and the boundary conditions that dictate the reflection and transmission of particles. The key takeaway is understanding how the energy of a particle and the potential of the barrier influence the behavior of particles at boundaries in quantum mechanics.

05:00
🔄 Particle Behavior in Quantum Barriers

The second paragraph wraps up the discussion on particle behavior in the presence of a potential barrier, emphasizing that when a particle's energy is greater than or equal to the barrier's potential, particles can be transmitted and reflected. It clarifies that if the energy were equal to the barrier's potential, no transmission would occur, and all particles would be reflected. The summary underscores the importance of understanding these dynamics for a comprehensive grasp of quantum mechanics.

Mindmap
Keywords
💡Quantum Mechanical World
The quantum mechanical world refers to the realm of physics where quantum mechanics is applied to understand and predict the behavior of particles at a microscopic level. In the context of the video, it is the domain where wave equations and energy barriers play a crucial role in determining the behavior of particles, such as their transmission and reflection at boundaries.
💡Wave Equation
The wave equation is a fundamental differential equation in physics that describes how waves, including matter waves in quantum mechanics, propagate through space and time. It is used to model the behavior of the wave function, which represents the probability amplitude of finding a particle at a certain location.
💡Energy
In the context of the video, energy refers to the total energy possessed by a particle, which is influenced by the potential of the barrier it encounters. The energy of a particle determines its behavior, such as whether it can be transmitted through or reflected by the barrier.
💡Potential Barrier
A potential barrier is a region in space where the potential energy is higher than the energy of a moving particle. In quantum mechanics, potential barriers can affect the transmission and reflection of particles, as they can either stop or partially block the particle's movement.
💡Wave Function
The wave function is a mathematical function that describes the quantum state of a particle in a quantum mechanical system. It contains all the information about the particle's probability distribution and is crucial for predicting the outcomes of quantum events.
💡Boundary Conditions
Boundary conditions are constraints applied to the solutions of differential equations at the edges of the region under consideration. In the context of the video, they are used to determine the coefficients in the wave equation, which in turn help in understanding the transmission and reflection of particles at the barrier.
💡Transmission
Transmission in the context of quantum mechanics refers to the phenomenon where particles can pass through a potential barrier, despite having less energy than the barrier's potential. It is one of the possible outcomes for particles encountering a barrier, as described by the wave equation.
💡Reflection
Reflection in quantum mechanics is the process where particles bounce back after encountering a potential barrier. It is a result of the wave equation's solutions indicating that part of the wave function moves in the opposite direction to how it was initially moving.
💡Wave Number
The wave number, denoted as k, is a measure of the spatial frequency of a wave, which in the context of the video, is related to the momentum of the particle in a quantum mechanical system. It is derived from the energy of the particle and the properties of the barrier.
💡Coefficients
Coefficients in the context of the wave equation are constants that multiply the exponential terms to determine the form of the wave function. They are crucial in solving the wave equation and are determined by applying boundary conditions.
Highlights

The lecture focuses on quantum mechanics, specifically at the boundary where a particle's energy is greater than the potential barrier.

The wave equation is explored in detail, particularly how it handles the situation when a particle's energy exceeds the barrier's potential.

The differential equation of the wave equation is defined, with the second derivative equal to minus k1 squared times the wave equation.

k1 is defined as the square root of 2m times energy (e) divided by h-bar, representing the wave function or wave number of the particle.

Once the particle crosses to the other side of the barrier, its total energy decreases due to the potential of the barrier.

The wave equation changes to minus k2 squared after the particle crosses the barrier, with k2 defined as 2m times the quantity minus V.

The energy on the other side of the barrier is less, hence k2 is smaller, leading to larger waves.

Both reflection and transmission of particles occur even when the particle's energy is greater than the barrier's potential.

The general solution to the wave equations is provided, with different coefficients and wave numbers on either side of the barrier.

In region two, no particles are expected to be moving to the left, thus the coefficient D must be zero.

Boundary conditions at x equals zero are discussed, requiring the wave functions on both sides of the barrier to be equal.

The number of reflected particles is determined by the relative energy on both sides of the boundary, using the K factor.

If k2 equals zero, it means the particle's energy equals the potential of the barrier, and none of the particles are transmitted; all are reflected.

When the particle's energy is greater than the barrier's potential, some particles are transmitted, as indicated by k1 times a being greater than k2 times C.

Understanding the concepts, variables, and constants in the wave equations is crucial for comprehending quantum mechanics at boundaries.

The lecture aims to help viewers understand how to deal with quantum mechanical situations where a particle's energy is greater than or equal to the potential of a barrier or step.

Transcripts

Browse More Related Video

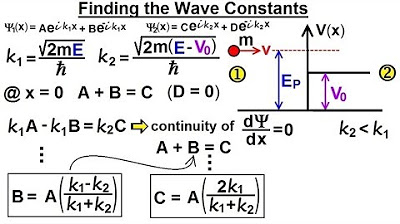
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (65 of 92) Wave Constants B=? C=?

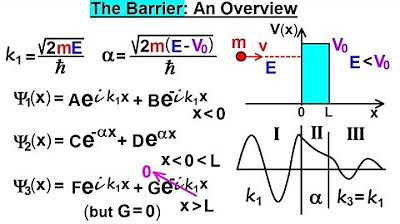
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (77 of 92) The Barrier: An Overview

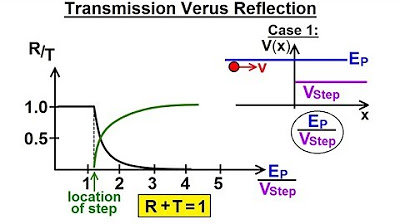
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (62 of 92) Transmission vs Reflection

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (76 of 92) Penetration Depth V0, E: Ex.

23. Quantum Mechanics V: Particle in a Box

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (74 of 92) R=? T=? V0=(3/4)E,.(Ex. 4 of 4)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
QuantumMechanicsWaveEquationsParticleBarrierEnergyTransmissionPhysicsLectureOnlineLearningEducationalContentScientificExplorationBarrierDynamicsWaveFunction