AP Daily: AP Calculus BC (1.1)
TLDRIn this introductory AP Calculus lesson, Brian Pass explores the concept of instantaneous rate of change, contrasting it with the average rate of change. He uses a road trip example to illustrate how average velocity can be calculated and then refines the concept to find instantaneous velocity by considering smaller and smaller time intervals. The lesson concludes with the key takeaway that the instantaneous rate of change corresponds to the slope of the tangent line to a function at a specific point, providing a foundation for further understanding of calculus.
Takeaways
- 📚 Introduction to Calculus: The video begins an exploration of calculus, focusing on the concept of change that can occur instantaneously.
- 👨🏫 Instructor Background: Brian Pass, a high school teacher from Speedway, Indiana, introduces himself and shares a personal anecdote about being a runner-up in a 5th-grade spelling bee.
- 🕒 Understanding Instantaneous Change: An 'instant' in mathematics is described as an infinitely small amount of time, which is crucial for grasping instantaneous rate of change.
- 📈 Average Rate of Change: The average rate of change of a function is the slope of the interval, calculated as (y2 - y1) / (x2 - x1), a concept from algebra.
- 🚗 Road Trip Example: The video uses a road trip scenario to illustrate how average velocity can be calculated and how it differs from instantaneous velocity.
- 📊 Instantaneous Velocity: The speedometer in a car provides an example of instantaneous velocity, which is the speed at a specific moment in time.
- 🔢 Calculating Instantaneous Velocity: By measuring the distance traveled over increasingly smaller time intervals, the average velocity approaches the instantaneous velocity.
- 📉 High School Population Example: The script presents an example of using the average rate of change to estimate the instantaneous rate of change for a high school's population over time.
- 🤔 Conceptual Challenge: The idea of calculating average velocity when time is zero (or virtually zero) introduces the concept of a limit, which is fundamental to calculus.
- 🔍 Tangent Line and Instantaneous Rate of Change: The slope of the tangent line to a function at a point represents the instantaneous rate of change at that point.
- 🎉 Final Fun Fact: Brian Pass shares the word he missed in the spelling bee—pneumonia—which he now spells correctly and has not missed since.
Q & A
What is the main topic of the first video in the AP Calculus series?
-The main topic of the first video is introducing calculus and the concept of change occurring at an instant.
Who is the instructor for the AP Calculus video series?
-The instructor for the AP Calculus video series is Brian Pass, a high school teacher in Speedway, Indiana.
What was Brian Pass's fun fact about himself in the video?
-Brian Pass shared that he was the runner-up in his school's spelling bee when he was in 5th grade.
What does the term 'instantaneous rate of change' refer to in the context of calculus?
-In calculus, 'instantaneous rate of change' refers to the rate of change at a specific point, which is the slope of the tangent line to a function at that point.
How is the average rate of change of a function calculated?
-The average rate of change of a function is calculated by finding the slope of the function over a given interval, which is the change in y (y2 - y1) divided by the change in x (x2 - x1).
How does the concept of average velocity relate to the concept of average rate of change?
-The concept of average velocity is similar to the average rate of change. It is calculated by dividing the total change in distance by the total change in time, providing an average speed over a period of time.
What is the relationship between average velocity and instantaneous velocity?
-Instantaneous velocity is the speed of an object at a specific instant in time, whereas average velocity is the speed calculated over a period of time. Instantaneous velocity can be thought of as the limit of average velocity as the time interval approaches zero.
How did Brian Pass estimate his instantaneous speed during a road trip?
-Brian Pass estimated his instantaneous speed during a road trip by calculating his average speed over increasingly smaller time intervals, such as one second, 0.1 seconds, and even smaller fractions of a second, until the time interval approached zero.
What is the significance of the tangent line in the context of instantaneous rate of change?
-The tangent line to a function at a specific point is significant because its slope represents the instantaneous rate of change at that point, indicating the direction and steepness of the function's change at that precise location.
How did Brian Pass use the concept of instantaneous rate of change to approximate the number of people in a high school from 7 a.m. to 8 a.m.?
-Brian Pass used the concept of instantaneous rate of change by finding the slopes (average rates of change) over very small time intervals around the time point of interest (20 minutes). This approximation gives an estimate of the instantaneous rate of change at that specific time.
What did Brian Pass reveal as the word he missed in the 5th-grade spelling bee?
-Brian Pass revealed that he missed spelling the word 'pneumonia' in the 5th-grade spelling bee, which led to him placing as the runner-up.
Outlines
📘 Introduction to Calculus and Instantaneous Rate of Change
The video begins with an introduction to the topic of calculus, emphasizing the concept of change occurring instantaneously. The speaker, Brian Pass, shares a personal anecdote about being a runner-up in a spelling bee in 5th grade. He then delves into the mathematical concepts of instantaneous and average rate of change, using the analogy of a road trip to explain how average velocity is calculated and how it relates to instantaneous speed. The discussion includes the idea of an 'instant' in mathematics, which is an infinitely small amount of time, and how this concept is fundamental to understanding calculus.
🔢 Understanding Instantaneous Speed and Rate of Change
This paragraph further explores the concept of instantaneous speed and rate of change. Brian uses the example of a car trip to illustrate how instantaneous speed can be approximated by calculating average velocity over increasingly smaller time intervals. He explains how these calculations can lead to the understanding of the instantaneous rate of change, which is the slope of the tangent line to a function at a specific point. The video concludes with a practical example of estimating the instantaneous rate of change for the number of people in a high school from 7 a.m. to 8 a.m., and emphasizes that the instantaneous rate of change is the limit of the average rate of change as the time interval approaches zero.
Mindmap
Keywords
💡Calculus
💡Instantaneous Rate of Change
💡Average Rate of Change
💡Odometer
💡Speedometer
💡Tangent Line
💡Slope
💡Road Trip
💡Instant
💡Average Velocity
💡Instantaneous Velocity
Highlights
Introduction to the concept of calculus and instantaneous change.
Instructor's personal anecdote about being a runner-up in a spelling bee.
Defining an instant as an infinitely small amount of time.
Exploring the difference between average rate of change and instantaneous rate of change.
The average rate of change formula: (y2 - y1) / (x2 - x1).
Calculating average velocity using distance and time elapsed.
The concept of instantaneous velocity as seen on a car's speedometer.
Using a hypothetical machine to measure distance traveled over time to approximate instantaneous speed.
The idea of shrinking time intervals to approach the concept of instantaneous speed.
Estimating the instantaneous rate of change by finding slopes at closely related points.
The tangent line's slope representing the instantaneous rate of change at a point.
The importance of understanding instantaneous rate of change in calculus.
Practical application of calculus concepts through a road trip example.
The use of calculus in real-world scenarios such as tracking population changes in a high school.
The method of approximating instantaneous rates of change by reducing time intervals.
The significance of the slope of the tangent line in determining instantaneous change.
Revealing the word 'pneumonia' as the one that caused the instructor's spelling bee loss.
Transcripts
Browse More Related Video

Understanding Differentiation Part 2: Rates of Change
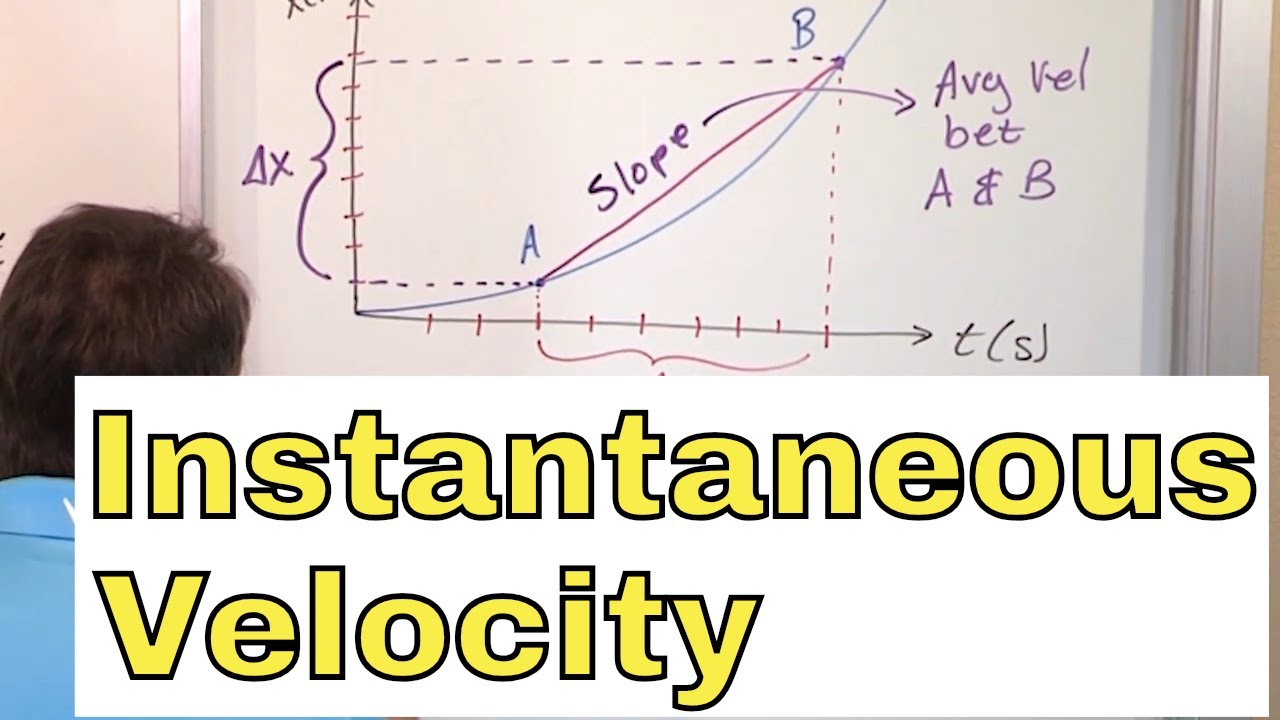
07 - What is Instantaneous Velocity?, Part 1 (Instantaneous Velocity Formula & Definition)

AP Daily: AP Calculus AB (1.1)
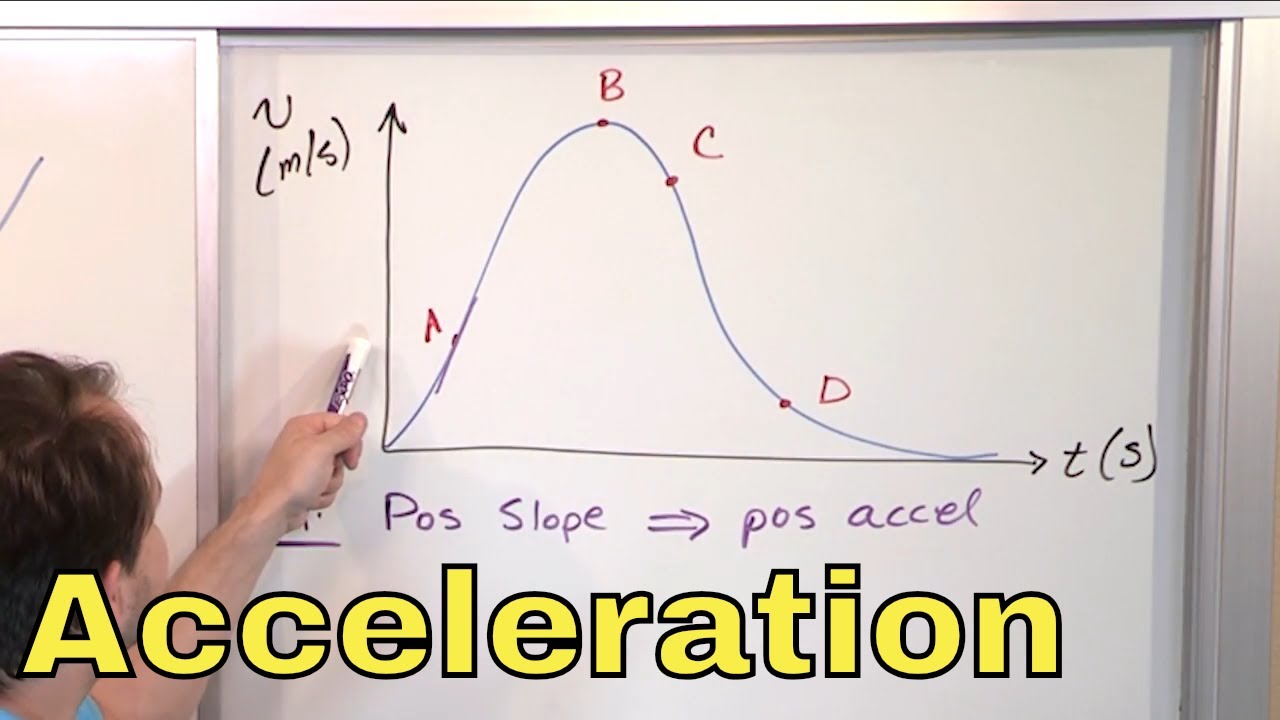
13 - Instantaneous Acceleration Explained (Average Vs. Instantaneous Acceleration)

Business Calculus - Math 1329 - Section 2.1 - The Derivative
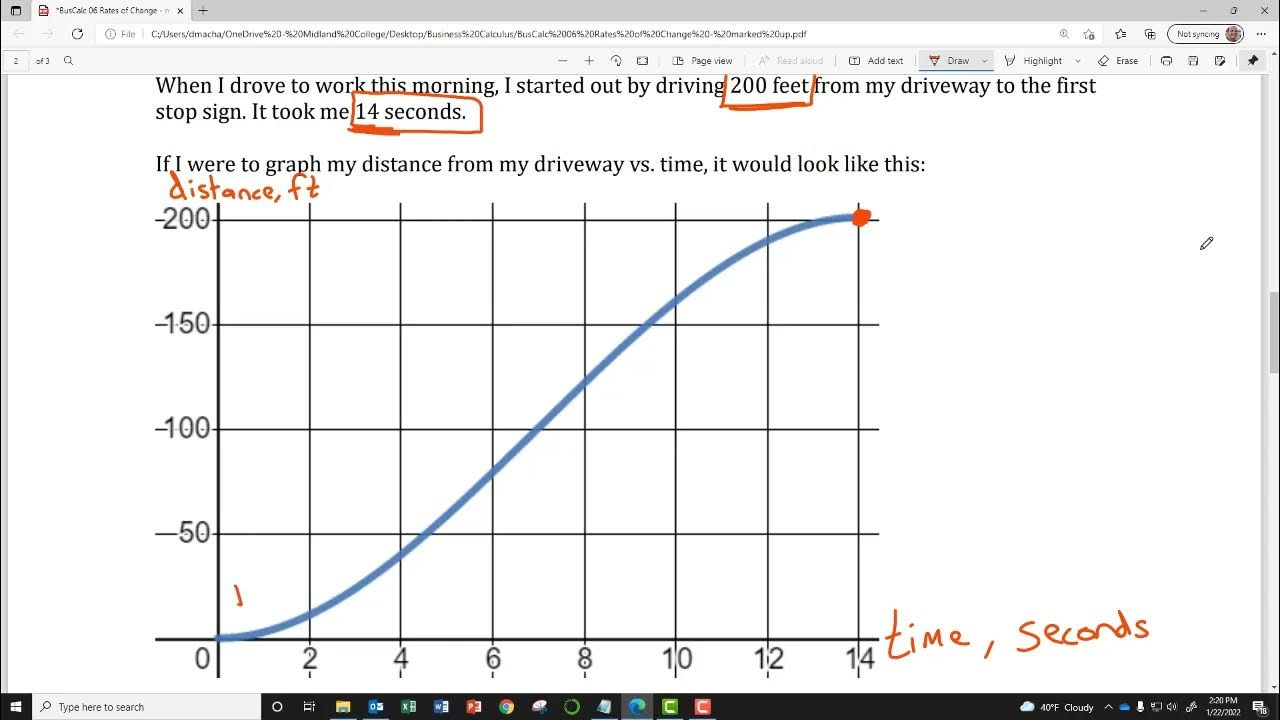
BusCalc 06 Rates of Change
5.0 / 5 (0 votes)
Thanks for rating: