AP Daily: AP Calculus AB (1.1)
TLDRIn this engaging video, Mark Corelli introduces the concept of limits in calculus, which are essential for understanding the instantaneous rate of change. He explains that limits allow us to generalize knowledge about average rates to instantaneous rates, emphasizing the idea of a function approaching a specific value rather than focusing on the value at a particular point. The video uses the example of a cubic function to illustrate how we can estimate the rate of change at a point by examining the slopes of secant lines as they get closer to the point of interest. Corelli demonstrates that as the points get closer together, the slope of the secant line approaches a limit, which is the instantaneous rate of change at that point. This concept is crucial for understanding calculus and will be explored further throughout the course.
Takeaways
- 📚 Calculus uses limits to generalize knowledge from average rates to instantaneous rates of change.
- 🤔 A limit in mathematics refers to the value a function approaches as the independent variable approaches a specific value.
- 👉 The concept of 'approach' is emphasized, indicating the function gets closer to a value without necessarily reaching it.
- 🔍 In calculus, we focus on what the function values are approaching, rather than the exact value at a specific point.
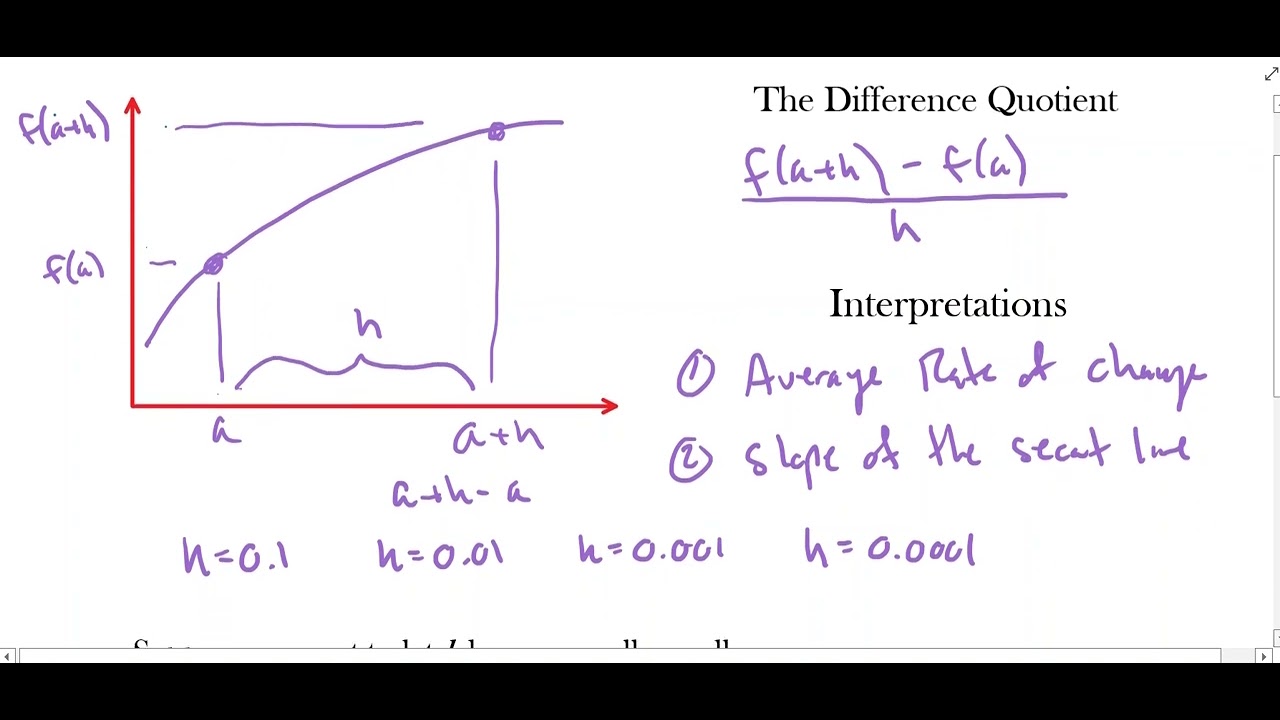
- 📈 The tangent line problem introduces the concept of the rate of change at a specific point on a curve, which is estimated by the slope of a secant line through two points.
- 📉 As the points used to calculate the secant line get closer, the slope of the secant line approaches the slope of the tangent line at that point.
- 🔢 By creating a table of values, we can observe the trend in the slope of secant lines and predict the limit of the slope as the points get infinitely close.
- 📊 The limit of the slope of secant lines as they get closer together is considered the instantaneous rate of change of the function at a specific point.
- ⛓ The process of finding limits is not just about finding a specific numerical value, but also about understanding the behavior of a function as it approaches a certain point.
- 🚫 The traditional method of finding the rate of change between two points (using slope) is not applicable when we want to find the rate of change at a single point, hence the need for limits.
- ⏳ The concept of limits and instantaneous rate of change is a fundamental idea in calculus that will be revisited and built upon throughout the course.
Q & A
What is the main concept introduced in the video?
-The main concept introduced in the video is the use of limits in calculus to generalize knowledge about average rates to the concept of instantaneous rate of change.
What does the term 'limit' refer to in the context of calculus?
-In calculus, a limit refers to the value that a function approaches as the independent variable approaches a specific value. It is about how close the function values can get to a certain point without actually being at that point.
Why do we use limits to find the instantaneous rate of change?
-We use limits to find the instantaneous rate of change because it allows us to investigate the rate of change at a single point, which is not possible using the traditional method of finding the average rate of change between two points.
How does the concept of limits differ from the approach used in algebra?
-In algebra, the focus is on finding the function value at a specific point. In contrast, calculus with limits is concerned with the behavior of the function as it approaches a certain point, not the value at the point itself.
What is the purpose of using a secant line to estimate the rate of change?
-A secant line is used to estimate the rate of change when we do not know how to find the change at a single point. By choosing two points that are very close together, we can approximate the rate of change at a specific point on the curve.
How does the slope of the secant line relate to the concept of limits?
-As the distance between the two points used to draw the secant line decreases (i.e., as 'a' gets closer to 'x'), the slope of the secant line approaches the slope of the tangent line at that point. This limiting value of the slope is the instantaneous rate of change.
What is the significance of the tangent line in the context of the video?
-The tangent line represents the exact rate of change of the curve at a specific point. It is derived from the concept of limits, as it is the line that 'touches' the curve at that point without crossing it.
What is the mathematical notation used to express the limit as x approaches a?
-The mathematical notation used to express the limit as x approaches a is 'lim (as x approaches a) f(x) = L', where 'L' is the value that the function f(x) approaches as x gets closer to 'a'.
Why is it not possible to use the slope formula directly when finding the rate of change at a single point?
-Using the slope formula directly when finding the rate of change at a single point leads to division by zero, as the denominator becomes (b - b), which equals zero. This is undefined in mathematics, hence the need to use limits to find the instantaneous rate of change.
What is the instantaneous rate of change at x equals a?
-The instantaneous rate of change at x equals a is the limit of the average rate of change between x and a as x gets infinitely close to a. It is represented as the value 'l' that 'm' approaches as b approaches a.
How does the concept of limits help in understanding the behavior of functions?
-The concept of limits helps in understanding the behavior of functions by allowing us to analyze what happens to the function as it approaches certain values or points where direct calculation might not be feasible or meaningful, such as at discontinuities or vertical asymptotes.
What can we infer from the increasing but slowing trend of the slopes in the table?
-The increasing but slowing trend of the slopes in the table suggests that the slope may be approaching a certain maximum value, which in this case is suspected to be 0.5. This indicates that the rate of change at that point on the curve is likely to be constant and does not exceed that value.
Outlines
📚 Introduction to Calculus and Limits
Mark Corelli introduces the concept of calculus, focusing on the use of limits to generalize knowledge about average rates to the concept of instantaneous rate of change. He explains that in calculus, a limit refers to the value a function approaches as the independent variable approaches a specific value. This is different from algebra where the focus is on the actual point. The video uses the example of a cubic function to illustrate how limits can be used to estimate the rate of change at a specific point by looking at the slope of secant lines that get progressively closer to the point of interest. The process involves creating a table of values to observe the trend as the points get closer and closer, ultimately suspecting that the limit of the slope of these secant lines is approaching a certain value. The video concludes with a visual confirmation of the limit using a tangent line and emphasizes the importance of limits in understanding the instantaneous rate of change.
🔍 The Role of Limits in Calculating Instantaneous Rate of Change
This paragraph delves into why limits are essential in calculus when dealing with the rate of change at a point. Traditionally, rate of change has been investigated between two points, but calculus aims to find the rate of change at a single point, which introduces the challenge of dividing by zero when the two points converge. To overcome this, the concept of a limit is used to find the value that the average rate of change approaches as the two points get infinitely close. The limit, in this case, is identified as the instantaneous rate of change of the function at a specific point 'a'. The paragraph emphasizes the significance of this concept, which will be a recurring theme throughout the course, and sets the stage for further exploration in subsequent topics and units.
Mindmap
Keywords
💡Calculus
💡Limits
💡Instantaneous Rate of Change
💡Function
💡Independent Variable
💡Secant Line
💡Tangent Line
💡Slope
💡Cubic Function
💡Approach
💡Instantaneous Rate of Change Formula
Highlights
Calculus uses limits to generalize knowledge about average rates to the concept of instantaneous rate of change.
A limit in mathematics refers to the value a function approaches as the independent variable approaches a specific value.
The concept of 'approach' is emphasized, indicating a function getting closer to a value without necessarily reaching it.
In algebra, the focus is on the actual point and function value, whereas calculus is interested in the trend as it approaches a point.
The tangent line problem introduces the challenge of finding the rate of change at a specific point on a curve.
Secant lines are used to estimate the rate of change around a point by calculating the slope between two points on the curve.
As the points used to calculate the secant line get closer, the slope of the secant line approaches the slope of the tangent line.
A table is used to systematically find the slopes of secant lines as the points get closer together, revealing a trend.
The limit of the slope of secant lines is suspected to approach a specific value, indicating the instantaneous rate of change at a point.
The concept of limits is crucial for finding the rate of change at a point, which can be problematic with traditional methods.
The instantaneous rate of change is represented by the limit as the distance between points approaches zero.
The slope of the tangent line is determined to be the instantaneous rate of change at a specific point on the curve.
The relationship between the limit of a secant line's distance and the slope of a tangent line is a central theme in calculus.
The use of limits allows for the transition from average rates of change to instantaneous rates of change, which is a fundamental concept in calculus.
The video introduces the concept that will be revisited and expanded upon throughout the course, emphasizing its importance.
The video concludes with a teaser for the next installment, promising further exploration of the topic.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: