Business Calculus - Math 1329 - Section 2.1 - The Derivative
TLDRThe video script delves into the concept of the derivative, a fundamental topic in calculus, by first introducing the average rate of change (ARC) between two points of a function. It illustrates how ARC is calculated using the slope formula and its relevance to the secant line. The script then transitions into the instantaneous rate of change, which is the rate of change at a single point, and how it is derived from the ARC by taking the limit as the interval between points approaches zero. This leads to the introduction of the derivative, symbolized as f'(x), which is the limit of the difference quotient. The script provides several examples to demonstrate how to calculate the average and instantaneous rate of change for various functions, including profit over time and cost functions. It also explains how to find the equation of the tangent line at a specific point on a curve, using the derivative for the slope and the function value for the point. The video concludes with an exercise to categorize different scenarios as either average or instantaneous rates of change, or neither, reinforcing the understanding of these concepts.
Takeaways
- 📈 The concept of the derivative is central to calculus and is developed from an algebraic standpoint.
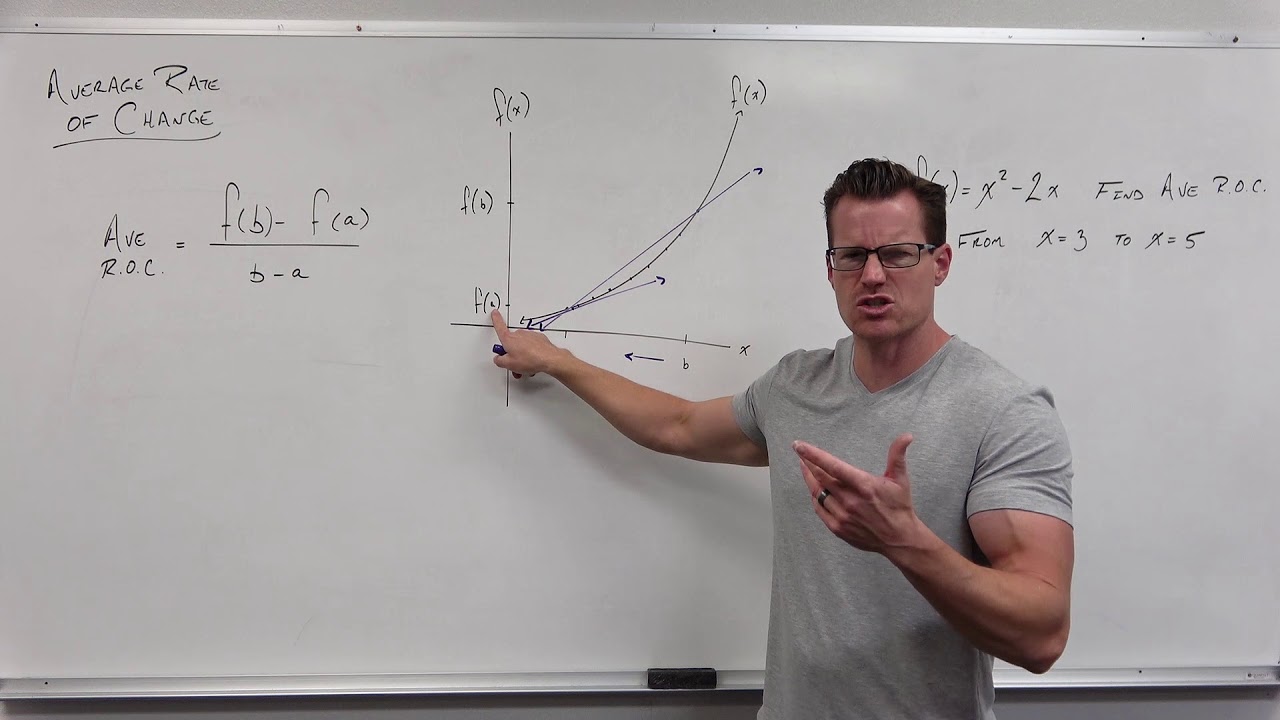
- 🔢 The average rate of change (ARC) is the rate of change between two points of a function and is equivalent to the slope of the secant line through those points.
- 📉 The ARC can be used to determine how fast a function, like profit over time, is rising on average, even if the function's curve is not straight.
- 💰 An example given is the total profit from laptops sold, which is calculated using a quadratic function, and the ARC is used to find the average profit change over a period.
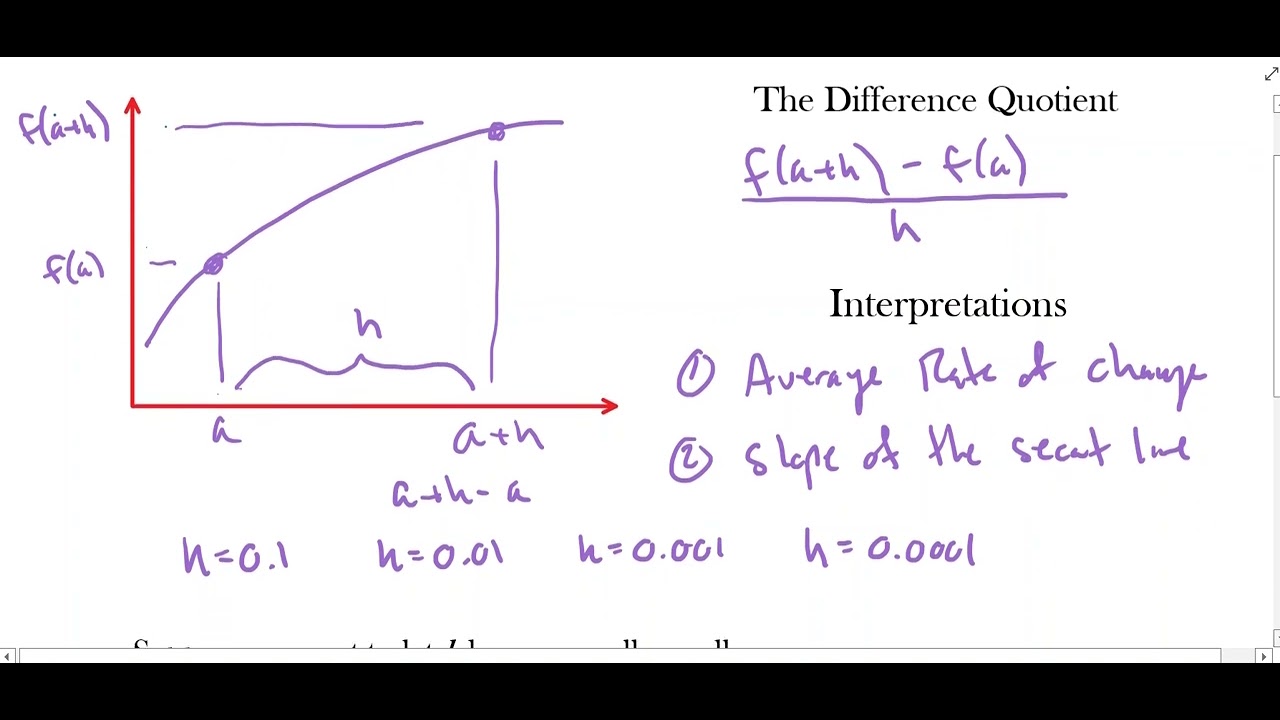
- 📚 The difference quotient is a formula derived from the ARC and is used to find the average rate of change between two points on a function.
- 🎓 The difference quotient simplifies to the derivative when considering the limit as the distance between the points (h) approaches zero.
- 🏗️ The derivative, represented as f'(x), is the instantaneous rate of change at a single point and is found by taking the limit of the difference quotient as h approaches zero.
- 📉 The derivative can be interpreted as the slope of the tangent line to a function at a given point, which gives the rate of change at that specific point.
- ✏️ The process of finding the equation of a tangent line involves calculating the derivative for the slope and using the function's value at a specific point for the coordinates.
- 🌐 Geogebra can be used to visualize the function, secant line, and tangent line, aiding in understanding the relationship between these concepts.
- ⚖️ The difference between average and instantaneous rates of change is that the average rate of change is calculated over a period or distance, while the instantaneous rate of change is the derivative at a specific point.
Q & A
What is the average rate of change (AROC) and how is it calculated?
-The average rate of change (AROC) is the rate of change between two points of a function. It is calculated using the slope formula, which is the difference in the Y values (f(X2) - f(X1)) divided by the difference in the X values (X2 - X1). It represents the slope of the secant line that passes through the two points on the function.
How does the average rate of change relate to the slope of a straight line?
-The average rate of change is essentially the slope of a straight line that would exist if the function's curve were to be straightened out over the interval between two points. It levels out the curve to provide a uniform rate at which the function increases or decreases over that interval.
What is the formula for the difference quotient?
-The difference quotient is a formula derived from the average rate of change and is represented as f(X + H) - f(X) / H, where H denotes the distance between the X values.
How is the difference quotient used to find the average rate of change in a function?
-The difference quotient is used to find the average rate of change in a function by plugging in the specific X values and H (the distance between those X values) into the difference quotient formula. The result is the average rate of change over the interval between the two X values.
What is the instantaneous rate of change and how is it found?
-The instantaneous rate of change is the rate of change at a single point. It is found by taking the limit of the difference quotient as H approaches zero. This process results in the derivative of the function, which represents the slope of the tangent line at that point.
How do you interpret the units of the average rate of change?
-The units of the average rate of change are derived from the units of the function's output divided by the units of its input. For example, if the function represents profit in dollars over time in weeks, the units would be dollars per week.
What is the significance of finding the derivative of a function?
-Finding the derivative of a function is significant because it provides the instantaneous rate of change at any point on the function. This can be used to analyze how a quantity is changing at a specific moment, which is crucial in various fields such as physics, engineering, and economics.
How does the derivative of a function relate to the tangent line at a point?
-The derivative of a function at a specific point is equal to the slope of the tangent line to the function at that point. The tangent line touches the function at exactly one point, and its slope represents the instantaneous rate of change at that point.
What is the process to find the equation of the tangent line to a function at a given point?
-To find the equation of the tangent line, you first find the derivative of the function to get the slope of the tangent line. Then, you find the function value at the given point to get the coordinates of the point of tangency. Using the slope-point form of a line (y - y1 = m(x - x1)), you can then write the equation of the tangent line.
How can you determine if a given scenario represents an average rate of change, an instantaneous rate of change, or neither?
-To determine the type of rate of change, consider whether the scenario involves a change over a period (average rate of change) or at a specific moment (instantaneous rate of change). If there is no change involved, it is neither. For example, the speed of a car over a trip is an average rate of change, the speed at a specific moment is an instantaneous rate of change, and the total distance traveled is neither.
What is the geometric interpretation of the derivative and how does it relate to the concept of a tangent line?
-The geometric interpretation of the derivative is the slope of the tangent line to a curve at a given point. As the derivative is the limit of the average rate of change as the interval shrinks to zero, it represents the instantaneous rate of change at that point. The tangent line is the line that just touches the curve at that point without crossing it, and its slope is given by the derivative.
Outlines
📘 Introduction to the Concept of Derivative
This paragraph introduces the concept of the derivative, central to the course, starting from an algebraic perspective. It explains the average rate of change (AROC) using a simple algebraic function, describing how to calculate the slope of a secant line between two points on a curve. The example given involves the profit from laptop sales over weeks, showing how to calculate profit after specific periods and the average rate of change in profit using the slope formula.
📏 Transition from AROC to Difference Quotient
The second paragraph delves deeper into the average rate of change, introducing the concept of the difference quotient. It transitions from specific x-values to using a new variable 'h' representing the distance between x-values, leading to a more generalized expression for the average rate of change. This is illustrated with the profit function of laptops, where calculations are shown in detail, including squaring and distributing terms to obtain the difference quotient for given weeks.
🧮 Detailed Analysis of the Difference Quotient
In this section, the focus is on calculating the difference quotient for the profit function using a step-by-step algebraic manipulation. It emphasizes the cancelation of terms and simplification, showing how to factor out common variables. The importance of precise calculations in deriving the quotient is highlighted, along with a real-world application to calculate the average rate of change between two time points using this new method.
🔍 Understanding Instantaneous Rate of Change
This paragraph introduces the concept of instantaneous rate of change, explaining how it differs from the average rate of change by focusing on a single point rather than an interval. It discusses the use of limits to find the derivative, symbolized as f prime of x, which is the slope of the tangent line at a point. The paragraph ends with a practical example calculating the instantaneous rate of change for laptop profit at four weeks using the derivative.
📈 Calculating and Interpreting Derivatives
The paragraph covers the derivation of the instantaneous rate of change in the context of cost functions for manufacturing cell phones. It explains how to calculate the derivative using limits and shows the step-by-step process of evaluating the function at specific points. Interpretations of these calculations are provided to understand how costs change as production levels vary, with specific examples for 20 cell phones.
📊 Real-World Application of Calculus Concepts
This section applies calculus concepts to understand and interpret real-world situations like city population growth. It explains how to calculate and interpret derivatives in practical contexts, showing the population growth of a city and the manufacturing cost of cell phones. The explanations include graphical representations, emphasizing the practical utility of calculus in predicting trends and making informed decisions based on mathematical analysis.
Mindmap
Keywords
💡Derivative
💡Average Rate of Change (ARO)
💡Secant Line
💡Difference Quotient
💡Instantaneous Rate of Change
💡Limit
💡Tangent Line
💡Profit Function
💡Daily Cost Function
💡Conjugate
💡GeoGebra
Highlights
The concept of the derivative is introduced as the central topic of the course.
Derivatives are developed from an algebraic standpoint before moving into calculus.
Average rate of change (AROC) is defined as the rate of change between two points of a function.
The formula for AROC is presented as the difference in Y values divided by the difference in X values.
The secant line, which passes through two points on a function, is equated with the average rate of change.
The average rate of change is used to determine the rate of increase of a function over a distance, as if it were a straight line.
An example of calculating total profit after 4 and 10 weeks using a profit function is provided.
The difference quotient is introduced as a concept derived from the average rate of change.
The difference quotient formula is established using a new variable H for the distance between X values.
The average rate of change in profit between 4 and 10 weeks is calculated using the difference quotient.
The instantaneous rate of change at a single point is defined as the derivative, obtained by taking the limit as H approaches zero.
The derivative is identified as the slope of the tangent line, representing the instantaneous rate of change.
An example demonstrates finding the instantaneous rate of change in a laptop profit function at a specific week.
The daily cost function for manufacturing cell phones is differentiated to find the derivative, representing cost changes.
The values of the cost function and its derivative at a specific production level are calculated and interpreted.
The equation of the tangent line to a function at a given point is found using the derivative for the slope and the function value for the point.
The process of finding the derivative of a square root function and using it to determine the tangent line equation is detailed.
The concept of categorizing different scenarios as average rate of change, instantaneous rate of change, or neither is discussed with examples.
The importance of using the correct language for interpreting rates of change is emphasized, including the use of positive numbers and descriptive terms.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: