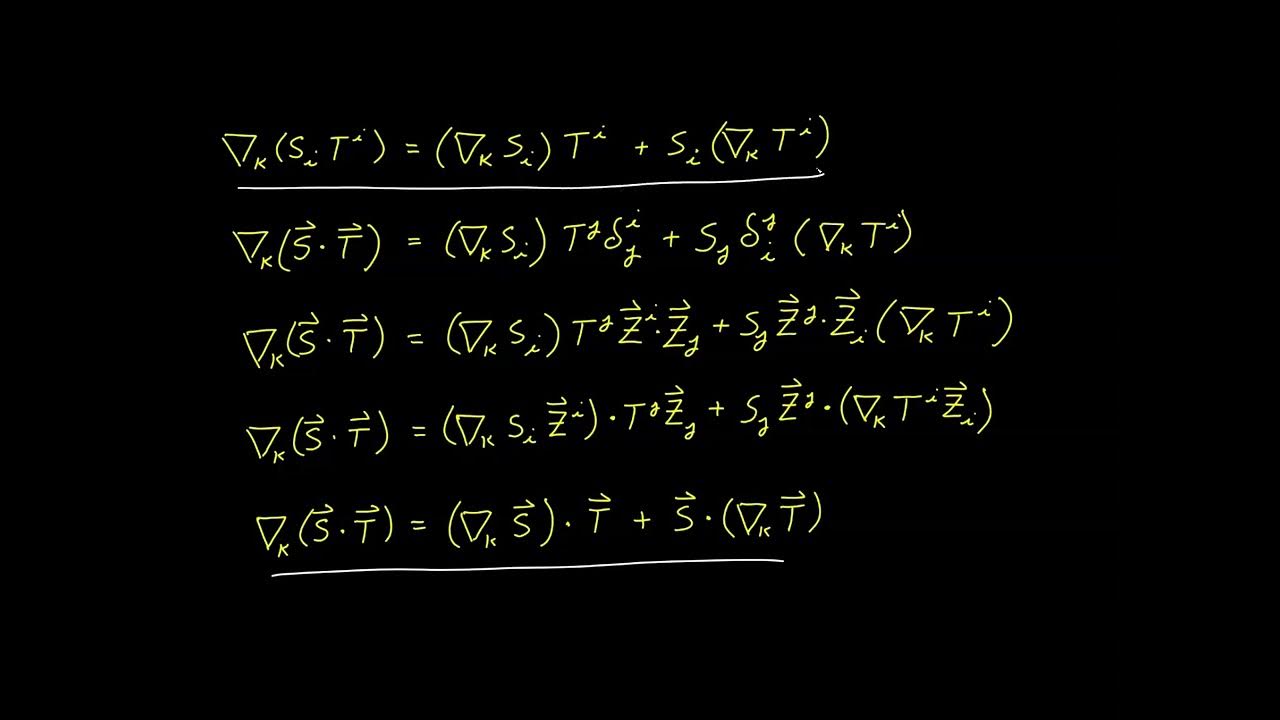Video 15 - Covariant Metric Tensor
TLDRIn this 15th installment of tensor calculus, the video delves into the covariant metric tensor, leveraging the dot product discussed in the previous session. It begins by differentiating a composite function using the chain rule, leading to the introduction of the covariant basis vector. The script then explains the metric equation, which links the infinitesimal distance along a curve to the coordinate system's properties. The video concludes by demonstrating how to calculate the arc length of a curve using the metric equation, emphasizing the importance of the covariant metric tensor as a conversion factor between coordinate system increments and Euclidean space.
Takeaways
- 📚 The video introduces the concept of the covariant metric tensor in the context of tensor calculus.
- 🔍 The covariant metric tensor is defined as the dot product of basis vectors \( \mathbf{z_i} \) and \( \mathbf{z_j} \).
- 🔑 The covariant metric tensor is also known as the fundamental tensor and is crucial for further analysis in tensor calculus.
- 🔄 The tensor is symmetric, meaning the order of indices does not affect its value, i.e., \( z_{ij} = z_{ji} \).
- 📈 The script demonstrates the use of the chain rule in composite functions for derivatives, particularly with respect to \( s \) and \( t \).
- 📉 The dot product is used to simplify expressions and is shown to be scalable, allowing for scalar factors to be separated from the vector components.
- 📐 The metric equation \( ds^2 = z_{ij} dz_i dz_j \) is derived, which relates the infinitesimal distance along a curve to the coordinate system's differentials.
- 🌐 The metric equation is essential for understanding the properties of the space being analyzed, serving as a measure of the space's geometry.
- ➿ The video explains how to derive the arc length of a curve by integrating the square root of the metric equation over a parameter range.
- 📝 The process of integrating the metric equation to find arc length involves separating variables and integrating from a starting to an ending parameter value.
- 🔍 The covariant metric tensor acts as a conversion factor, allowing the relationship between the Euclidean space distance and the coordinate system to be determined.
Q & A
What is the main topic of the video?
-The main topic of the video is the introduction of the covariant metric tensor in the context of tensor calculus.
What mathematical concept is used to derive the covariant metric tensor?
-The dot product is used to derive the covariant metric tensor by taking the dot product of the basis vectors with each other.
What is the significance of the covariant metric tensor in tensor calculus?
-The covariant metric tensor is significant because it plays an important role in various calculations and is referred to as the fundamental tensor.
Why is the covariant metric tensor considered a second rank tensor?
-The covariant metric tensor is considered a second rank tensor because it has two indices, indicating that it is a type of tensor that can transform in a specific way under coordinate transformations.
What property of the covariant metric tensor is highlighted in the script?
-The script highlights the property of symmetry in the covariant metric tensor, meaning that the tensor remains the same when its indices are swapped.
What is the metric equation derived from the covariant metric tensor?
-The metric equation derived from the covariant metric tensor is an equation that relates the infinitesimal distance along a curve to the differential changes in the coordinate system.
How does the metric equation relate to the concept of arc length?
-The metric equation is used to compute the arc length of a curve by integrating the differential form of the equation over a range of parameter values.
What is the role of the covariant metric tensor in calculating arc length?
-The covariant metric tensor acts as a conversion factor that relates the Euclidean space distance along the curve to the coordinate system's incremental values.
How does the video script describe the process of deriving the arc length from the metric equation?
-The script describes the process by taking the square root of both sides of the metric equation, multiplying by the differential of the parameter, and then integrating over the desired range.
What is the final formula provided in the script for calculating the arc length?
-The final formula for calculating the arc length is an integral of the square root of the covariant metric tensor components multiplied by the differential of the coordinate system values, integrated over a range of the parameter.
Outlines
📚 Introduction to Covariant Metric Tensor
This paragraph introduces the concept of the covariant metric tensor within the context of tensor calculus. The video begins by discussing the dot product and its application to composite functions. The derivative of 'r' with respect to 's' is taken using the chain rule, leading to an expression involving the unit vector tangent to the curve and the partial derivative of 'r' with respect to the coordinate value. The paragraph then delves into the dot product of both sides of the equation with itself, resulting in an expression that simplifies to the introduction of the covariant metric tensor, denoted as 'z,ij'. This tensor is defined as the dot product of the covariant basis vectors and plays a fundamental role in subsequent discussions. The explanation also covers the rules of tensor calculus, emphasizing the importance of not reusing dummy indices in a given term.
🔍 Properties and Definition of the Covariant Metric Tensor
The second paragraph focuses on the properties of the covariant metric tensor, which is defined as the dot product of the basis vectors 'zi' and 'zj'. It is highlighted that this tensor is of second rank and is symmetric, meaning the indices can be swapped without changing the value. The paragraph also introduces the concept of the metric equation, which relates the infinitesimal distance along a curve to the coordinate values through the covariant metric tensor. This equation is crucial as it provides a measure of the space's properties. Additionally, the paragraph discusses the process of deriving the arc length of a curve by integrating the differential form of the metric equation, emphasizing the role of the covariant metric tensor as a conversion factor between the coordinate system and Euclidean space.
📐 Application of the Metric Equation and Arc Length Calculation
The final paragraph summarizes the key takeaways from the video, emphasizing the definition and application of the covariant metric tensor. It reiterates the tensor's role in forming a second rank symmetric tensor with nine different terms resulting from the dot product of the basis vectors. The metric equation is presented as a fundamental relationship that connects the Euclidean distance along an arc to the coordinate values, with the covariant metric tensor serving as a conversion factor. The paragraph concludes by explaining how the arc length can be calculated using the metric equation, integrating the expression from a specific range of 't' values to obtain the Euclidean length of the curve. This method is essential for understanding the geometric properties of the space being analyzed.
Mindmap
Keywords
💡Dot Product
💡Covariant Metric Tensor
💡Composite Functions
💡Chain Rule
💡Partial Derivative
💡Unit Vector
💡Basis Vector
💡Metric Equation
💡Arc Length
💡Tensor Calculus
Highlights
Introduction of the covariant metric tensor using the dot product from the previous video.
Explanation of the chain rule for composite functions in tensor calculus.
Derivation of the relationship between composite functions using partial derivatives.
Identification of dr/ds as the unit vector tangent to the curve.
Clarification of the covariant basis vector and its role in tensor calculus.
Use of the dot product to form an equation involving the unit vector and covariant basis vectors.
Discussion on the importance of using different indices in tensor calculus to avoid confusion.
Expansion of the dot product into nine different terms for a comprehensive equation.
Introduction of the covariant metric tensor as a second rank tensor that is symmetric in its indices.
Definition of the metric equation and its significance in relating Euclidean distance to coordinate values.
Explanation of how the covariant metric tensor acts as a conversion factor between coordinate system values and Euclidean space.
Derivation of the formula to compute the length of an arc in a chosen coordinate system.
Emphasis on the practical application of the metric equation in calculating arc length.
Review of the major takeaways including the definition and properties of the covariant metric tensor.
Summary of the metric equation's role in tensor calculus and its importance in space analysis.
Highlight of the method to derive arc length, integrating the metric equation with respect to the parameter.
Anticipation of the next video's content, which will demonstrate the evaluation of these concepts in sample coordinate systems.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: