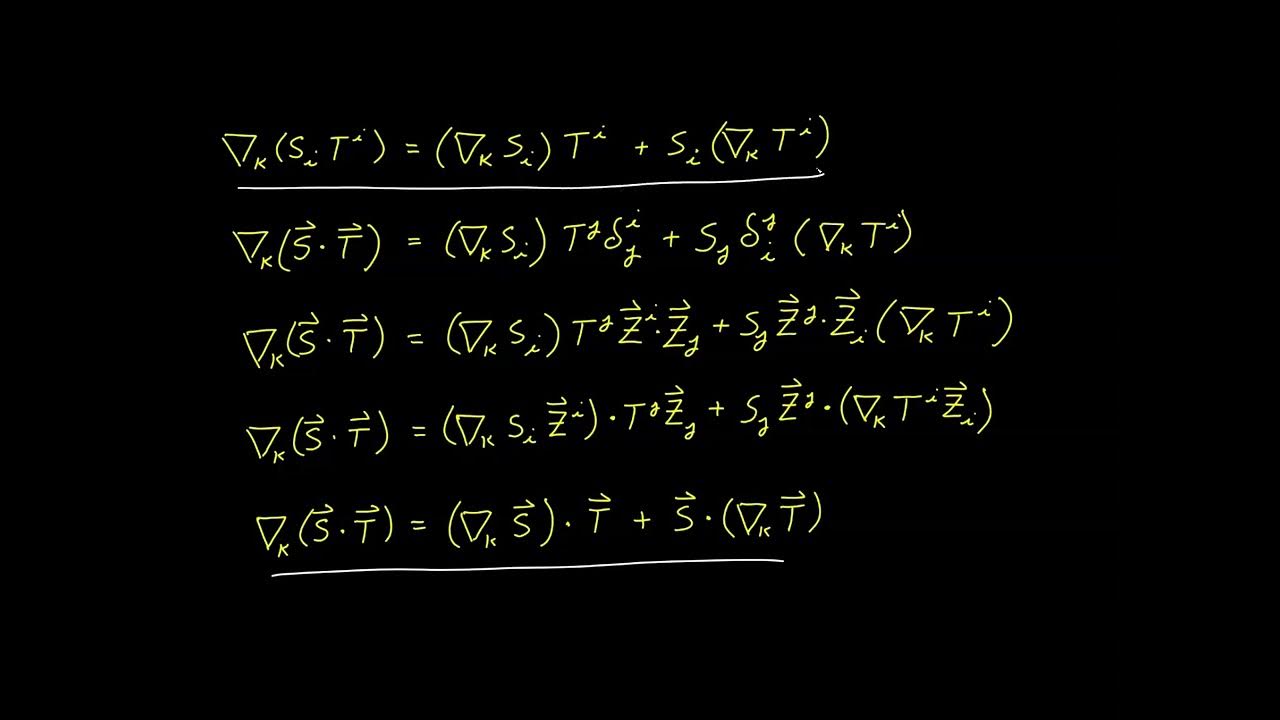Tensor Calculus For Physics Majors 006 | The Metric Tensor pt. 1
TLDRThis educational video script introduces the concept of the metric tensor, a fundamental aspect of tensor calculus, particularly for physics majors. It explains the distinction between coordinate displacement and distance, using different coordinate systems such as Cartesian, cylindrical, and spherical. The script delves into how the metric tensor converts coordinate displacements into distances and demonstrates this with the help of scalar equations. It also covers the calculation of the metric tensor components by taking the dot product of basis vectors in spherical coordinates, providing a deeper understanding of tensor calculus and its applications in physics.
Takeaways
- 📚 The video is an episode of 'Tensor Calculus for Physics Majors' focusing on the introduction of the metric tensor.
- 🔍 The script clarifies the distinction between coordinate displacement and distance, highlighting their differences in various coordinate systems.
- 📐 The metric tensor's role is to convert coordinate displacements into distances, which is fundamental in tensor calculus.
- 📈 The script introduces the concept of 'DS squared', representing the square of the distance, and explains its calculation in different coordinate systems.
- 📝 The video demonstrates the use of index notation to express 'DS squared' in a more compact form, initially facing challenges with the notation.
- 🧠 The inertia tensor is compared to the metric tensor, explaining how both tensors transform certain quantities into others with different units or directions.
- 📊 The metric tensor is represented as a square matrix for orthogonal systems, with off-diagonal components being zero due to the system's orthogonality.
- 📘 The script provides the matrix representations of the metric tensor for Cartesian, cylindrical, and spherical coordinates.
- 🔢 The components of the metric tensor are calculated by taking the dot product of the basis vectors in the coordinate system, which is a method introduced for spherical coordinates.
- 🔄 The video script discusses the transformation of the metric tensor when changing coordinate systems and the implications for its components.
- 🚀 The series promises to delve deeper into tensor calculus, including derivatives of tensors and the concepts of covariant and contravariant indices in future videos.
Q & A
What is the main topic of this video series?
-The main topic of this video series is tensor calculus, specifically focusing on the metric tensor and its application in physics, including its connection to special relativity and the concepts of contravariant and covariant indices.
What is the difference between coordinate displacement and distance?
-Coordinate displacement refers to the change in coordinates in a given system, which may not have units of length. Distance, on the other hand, is a scalar quantity that measures the length of the path between two points and has units of length.
What role does the metric tensor play in converting coordinate displacements into distances?
-The metric tensor converts coordinate displacements into distances by using the dot product of the displacement vector with itself, taking into account the specific properties of the coordinate system being used.
What is the purpose of the Einstein summation convention used in the script?
-The Einstein summation convention simplifies the notation by implying that repeated indices are summed over, allowing for a more compact representation of equations involving tensors.
How is the square of the distance, DS squared, defined in the context of the script?
-In the script, DS squared is defined as the dot product between the displacement vector and itself (dr dot dr), which results in a scalar quantity representing the square of the distance between two points.
What does the metric tensor represent in Cartesian coordinates?
-In Cartesian coordinates, the metric tensor is represented as the Kronecker delta, which is a matrix of ones on the diagonal and zeros elsewhere, indicating that the coordinate system is orthogonal and distances are calculated directly from the squares of the coordinate displacements.
What is the metric tensor for cylindrical coordinates and what does it imply?
-The metric tensor for cylindrical coordinates is represented as [1, 0, 0; 0, rho^2, 0; 0, 0, 1], which implies that the displacement in the radial direction (rho) does not directly contribute to the distance without being multiplied by rho, while the angular displacement (phi) contributes to the distance only when squared and multiplied by rho^2.
How are the components of the metric tensor calculated in spherical coordinates?
-The components of the metric tensor in spherical coordinates are calculated by taking the dot product of the basis vectors of the coordinate system, which are derived from the derivatives of the position vector with respect to each coordinate (r, theta, phi).
What is the significance of the off-diagonal components of the metric tensor in an orthogonal system?
-In an orthogonal system, the off-diagonal components of the metric tensor are zero, indicating that there are no cross terms in the distance calculation, as each coordinate displacement contributes independently to the total distance.
What is the relationship between the metric tensor and the inertia tensor mentioned in the script?
-Both the metric tensor and the inertia tensor are used to transform quantities from one form to another, with the metric tensor converting coordinate displacements into distances and the inertia tensor transforming angular velocity into angular momentum.
Outlines
📚 Introduction to Metric Tensor and Coordinate Systems
The script begins by introducing the concept of the metric tensor, a fundamental component of tensor calculus, which is essential for converting coordinate displacements into distances. The distinction between coordinate displacement and distance is clarified using the example of displacement vectors in Cartesian, cylindrical, and spherical coordinate systems. The importance of the metric tensor in handling different coordinate systems and its utility in transforming these displacements into distances is discussed. The script also introduces the concept of 'ds squared', the square of the distance, and its calculation in various coordinate systems using index notation.
🔍 The Metric Tensor's Role in Unit Transformation
This paragraph delves deeper into the role of the metric tensor in unit transformation, highlighting the need for a mechanism that can adjust units of coordinate displacements to become units of distance. The script discusses the failure of simple index notation to correctly represent distances in non-Cartesian coordinate systems and introduces the concept of the inertia tensor as a comparison. The metric tensor is then defined as a tool that can correctly transform coordinate displacements into distances by incorporating the correct units, and the Einstein summation convention is introduced to handle the tensor's components.
📘 Calculating the Metric Tensor for Different Coordinate Systems
The script explains how to calculate the components of the metric tensor for different coordinate systems, starting with the Cartesian system where the metric tensor is represented by the Kronecker delta. The cylindrical coordinate system's metric tensor is then derived, showing how it differs from the Cartesian system and how it correctly accounts for the units of distance. The process of calculating the metric tensor involves taking the dot product of the basis vectors in the coordinate system, and the script provides a step-by-step calculation for the cylindrical coordinate system.
🌐 Deriving the Metric Tensor for Spherical Coordinates
The script continues with the derivation of the metric tensor for spherical coordinates, starting with the definition of the position vector in spherical coordinates and the calculation of the basis vectors through differentiation. The metric tensor components are then found by taking the dot product of these basis vectors. The script outlines the calculation of the diagonal components of the metric tensor, which results in a diagonal matrix with specific components for R, Theta, and Phi, reflecting the nature of the spherical coordinate system.
🚀 Conclusion and Future Outlook on Tensor Calculus
In the final paragraph, the script wraps up by summarizing the importance of the metric tensor in spherical coordinates and its matrix representation. It also hints at future videos that will delve deeper into tensor calculus, including derivatives of tensors, covariant and contravariant indices, and the implications of raising and lowering indices. The script invites viewer feedback on the frequency and content of upcoming videos, emphasizing the series' focus on tensor calculus and its applications in physics.
Mindmap
Keywords
💡Tensor Calculus
💡Metric Tensor
💡Coordinate Displacement
💡Distance
💡Dot Product
💡Index Notation
💡Einstein Summation Convention
💡Orthogonal System
💡Cylindrical Coordinates
💡Spherical Coordinates
Highlights
Introduction to the concept of the metric tensor and its integral role in tensor calculus.
Difference between coordinate displacement and distance, with examples in Cartesian, cylindrical, and spherical coordinates.
Explanation of how the metric tensor converts coordinate displacements into distances.
Introduction of 'DS squared' as the square of the distance, calculated as the dot product of the displacement vector with itself.
Expression of DS squared for different coordinate systems, showing the basis for the metric tensor's utility.
Attempt to simplify the notation using index notation and the failure of the initial approach.
Successful simplification using the summation over diagonal indices to represent DS squared.
Discussion on the need for a tensor that can handle units of distance correctly in different coordinate systems.
Introduction of the metric tensor as the solution to correctly handle units and coordinate transformations.
Einstein summation convention's role in simplifying the expression of the metric tensor.
Matrix representation of the metric tensor for orthogonal systems, emphasizing the zero off-diagonal components.
Calculation of the metric tensor for Cartesian coordinates, showing its equivalence to the Kronecker delta.
Metric tensor for cylindrical coordinates and its impact on the calculation of DS squared.
Introduction to the process of calculating the components of the metric tensor using the dot product of basis vectors.
Detailed calculation of the metric tensor components for spherical coordinates.
Matrix representation of the metric tensor in spherical coordinates and its application to calculate DS squared.
Upcoming in-depth exploration of tensor calculus, including derivatives of tensors and the meaning of covariant and contravariant indices.
Engagement with the audience for feedback on the video series frequency and content preferences.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: