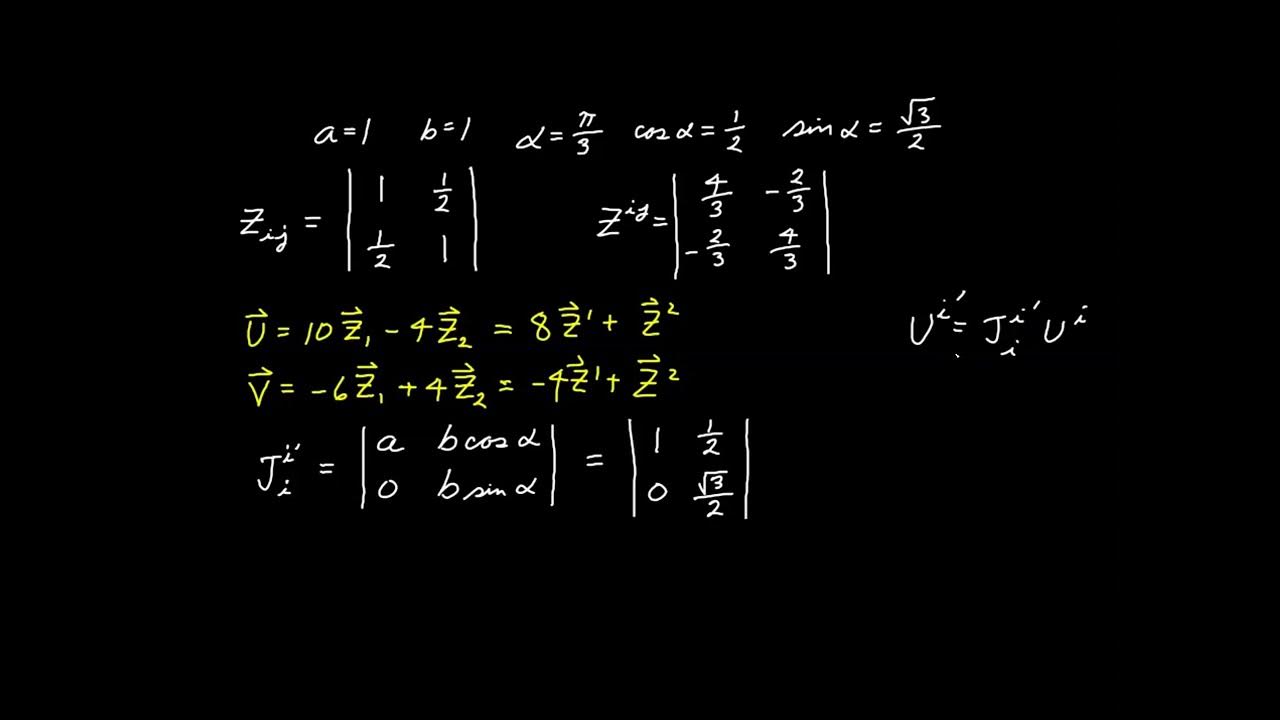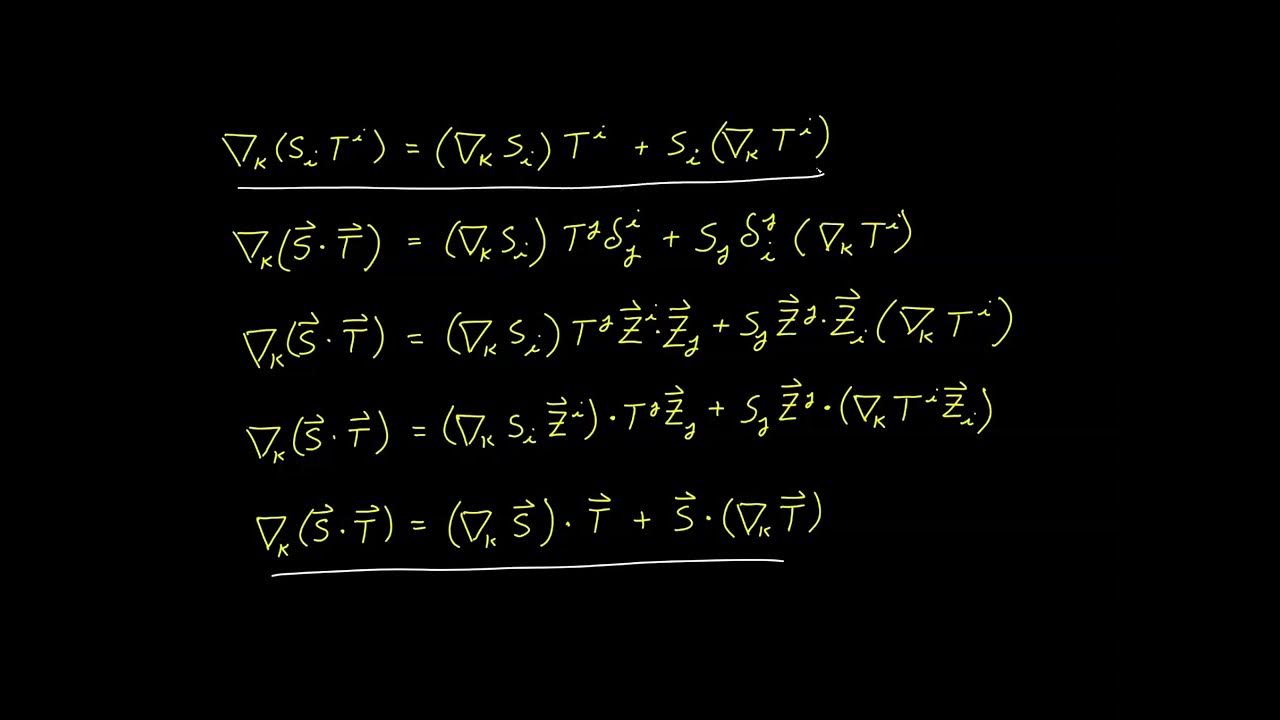Video 24 - Dot Product
TLDRIn this 24th tutorial on tensor calculus, the presenter derives an invariant relationship for the dot product using tensor calculus syntax. They explore various expressions for the dot product between two vectors, emphasizing the covariant and contravariant metric tensors. The video demonstrates that all four derived expressions are equivalent and invariant, meaning they hold true in any coordinate system. The presenter also highlights the application of these expressions in Cartesian coordinates, reinforcing the principle that if an invariant tensor equation works in one coordinate system, it must work in all. The video concludes with a discussion on how to develop a tensor equation by inspection, using the known dot product in Cartesian coordinates as a starting point.
Takeaways
- 📚 The video is part of a series on tensor calculus, focusing on deriving an invariant relationship for the dot product using tensor calculus syntax.
- 📐 The script discusses expressing vectors in terms of both covariant and contravariant basis, and explores the dot product between two vectors, vector u and vector v.
- 🔍 The derivation starts by using linear combinations of the basis vectors and dotting them with the vectors to find different expressions for the dot product.
- 🧠 The covariant metric tensor (g_ij) and the contravariant metric tensor (g^ij) are introduced as part of the expressions for the dot product.
- 🔢 The script shows that there are four different but equivalent ways to express the dot product in tensor calculus, all of which are invariant expressions.
- 🌐 The importance of the dot product as an invariant is emphasized, meaning it remains the same regardless of the coordinate system used.
- 🔄 The script explains that the different expressions for the dot product are essentially variations of the same concept, and the choice of which to use depends on the available vector components.
- 📈 The video demonstrates how the derived tensor expressions for the dot product apply to Cartesian coordinates, confirming the generality of the derived relationships.
- 📝 The principle that if an invariant tensor equation holds true for one coordinate system, it must hold true for all coordinate systems is highlighted.
- 🚀 The video suggests a method for deriving tensor equations by starting with a known expression in Cartesian coordinates and transforming it into a tensor equation that is valid in all coordinate systems.
- 🔑 The final takeaway is the recognition that the dot product can be represented as an invariant expression in tensor calculus, which is crucial for understanding its geometric properties across different coordinate systems.
Q & A
What is the main topic of this video in the series on tensor calculus?
-The main topic of this video is to derive an invariant relationship for the dot product in tensor calculus syntax.
What are the two vectors mentioned in the script, and how can they be expressed?
-The two vectors mentioned are vector u and vector v, and they can be expressed as linear combinations using either the covariant or contravariant basis.
What is the significance of using dummy indices in the script's mathematical expressions?
-Dummy indices are used to avoid reusing indices in summations, which helps to keep track of the terms in the expressions and ensures that the summation is performed correctly over all relevant indices.
What is the role of the covariant metric tensor in the expression for the dot product between two vectors?
-The covariant metric tensor, denoted as g_ij, is used to contract indices in the expression for the dot product, allowing for the calculation of the dot product in terms of the components of the vectors in the covariant basis.
What is the Kronecker delta, and how does it appear in the script?
-The Kronecker delta, denoted as δ_ij, is a tensor that is equal to 1 when its indices are equal and 0 otherwise. In the script, it is used to absorb an index, simplifying the expression for the dot product.
Why are the four different expressions for the dot product considered invariant?
-The four expressions are considered invariant because they are tensor equations with all indices contracted, meaning they do not depend on the choice of coordinate system and yield the same result regardless of the system used.
How does the script demonstrate that the derived expressions for the dot product are applicable to Cartesian coordinates?
-The script shows that by replacing the tensor components with their Cartesian counterparts and simplifying, the derived expressions for the dot product reduce to the standard Cartesian dot product formula, confirming their applicability.
What is the importance of the principle that if an expression is true for one coordinate system and is an invariant tensor equation, it must be true for all coordinate systems?
-This principle is crucial because it allows for the validation of tensor equations across different coordinate systems. If an equation is proven to be true in one system and is invariant, it guarantees its validity in all systems without the need for separate verification.
How can one derive a tensor equation for the dot product from its expression in Cartesian coordinates?
-One can derive a tensor equation for the dot product by recognizing that the Cartesian expression is a summation over the components of the vectors and then generalizing this to tensor notation, ensuring that the indices are properly contracted to form an invariant expression.
What does the script suggest about the relationship between the covariant and contravariant components of a vector in Cartesian coordinates?
-The script suggests that in Cartesian coordinates, the covariant and contravariant components of a vector are identical, meaning that the index position does not affect the component values.
Outlines
📚 Derivation of the Dot Product in Tensor Calculus
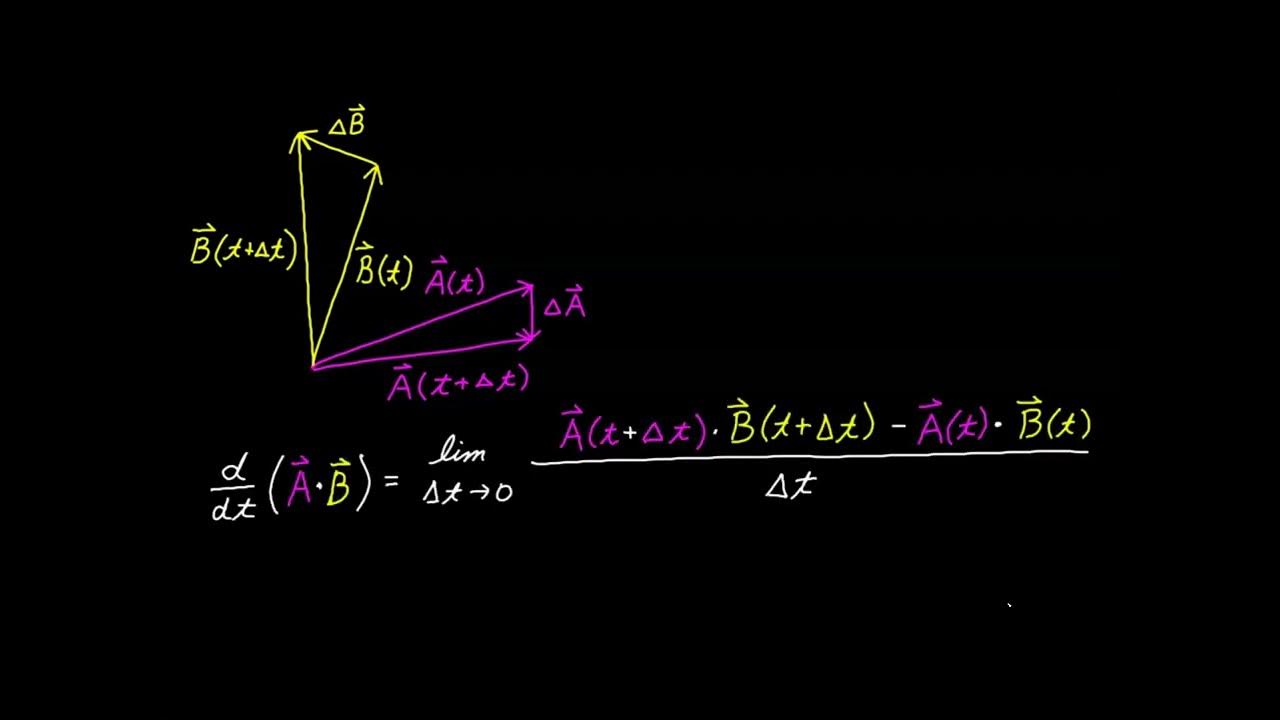
This paragraph introduces the derivation of an invariant relationship for the dot product in tensor calculus. The process begins with expressing two vectors, u and v, as linear combinations using either covariant or contravariant bases. The goal is to find an expression for the dot product, u·v, by combining these linear combinations and utilizing the metric tensor. The paragraph explains the steps to arrive at the dot product expression, including the use of dummy indices and the covariant metric tensor, ultimately leading to an invariant relationship.
🔍 Exploring Different Expressions for the Dot Product
The second paragraph delves into the exploration of different ways to express the dot product between two vectors in tensor calculus. It discusses the use of covariant and contravariant components and how they can be interchanged to derive equivalent expressions. The paragraph emphasizes that all indices in these expressions are dummy indices, resulting in tensor equations with contracted indices, which are invariant regardless of the coordinate system used. It also highlights the importance of the metric tensor and Kronecker delta in these expressions and how they relate to the dot product's invariance.
📈 Applying the Dot Product Relationship in Cartesian Coordinates
This paragraph focuses on applying the derived tensor relationship for the dot product to Cartesian coordinates. It explains how the components of vectors in Cartesian coordinates can be represented as either contravariant or covariant components without distinction. The paragraph demonstrates how the various tensor expressions for the dot product simplify in Cartesian coordinates, showing that they all result in the standard formula for the dot product in this coordinate system. It reinforces the principle that if an expression is an invariant tensor equation and holds true in one coordinate system, it must hold true in all coordinate systems.
🔧 Transforming Cartesian Dot Product into a Tensor Equation
The final paragraph discusses the process of transforming the Cartesian dot product expression into a tensor equation by inspection. It illustrates how recognizing the equivalence of contravariant and covariant components in Cartesian coordinates allows for the construction of a valid tensor equation. The paragraph explains that by identifying an expression that works in Cartesian coordinates and ensuring it is a tensor equation, one can guarantee its applicability in all coordinate systems. It concludes with the main takeaway that the dot product is an invariant expression and a geometric object, and that the derived tensor equation can be used to understand the dot product in various coordinate systems.
Mindmap
Keywords
💡Tensor Calculus
💡Dot Product
💡Vector
💡Covariant Basis
💡Contravariant Basis
💡Metric Tensor
💡Invariant Expression
💡Dummy Index
💡Cartesian Coordinates
💡Tensor Equation
Highlights
Introduction of deriving an invariant relationship for the dot product in tensor calculus syntax.
Expression of vectors u and v as linear combinations using covariant and contravariant bases.
Exploration of the dot product between two vectors using tensor calculus.
Use of the covariant metric tensor in the expression for the dot product.
Introduction of the contravariant metric tensor in the dot product expression.
Explanation of the Kronecker delta's role in simplifying the dot product expression.
Demonstration of four different ways to express the dot product between u and v.
Identification of invariant expressions in tensor equations with contracted indices.
Discussion on the invariance of the dot product as a geometric object.
Interchangeability of tensor expressions due to dummy index manipulation.
Application of the derived relationship to Cartesian coordinates for validation.
Confirmation that all four expressions result in the same dot product formula in Cartesian coordinates.
Principle that an invariant tensor equation valid in one coordinate system must be valid in all.
Technique of turning a known Cartesian coordinate expression into a tensor equation by inspection.
Derivation of the tensor equation for the dot product from the Cartesian coordinate expression.
Conclusion that the derived tensor equation for the dot product is an invariant and geometric object.
Highlight of the four equivalent forms of the dot product expression and their practical use cases.
Final takeaway summarizing the invariant nature of the dot product and its significance in various coordinate systems.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: