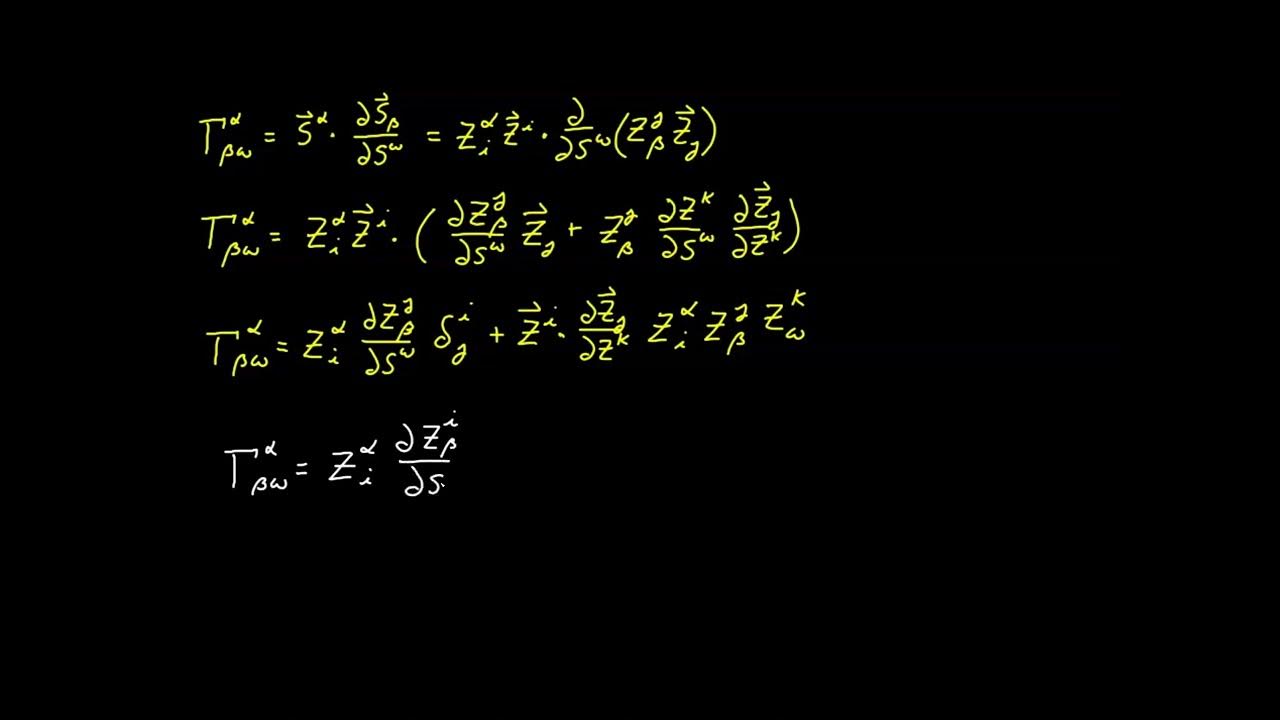Video 70 - Surface Christoffel Examples
TLDRIn this educational video, the presenter delves into the evaluation of Christoffel symbols for various sample surface manifolds using tensor calculus. Two methods are discussed: the direct computation using partial derivatives of the covariant metric tensor and contraction with the contravariant metric tensor, and a conversion method involving the ambient coordinate system's Christoffel symbols and shift tensor derivatives. The video provides step-by-step calculations for cylindrical, spherical, and torus surfaces, demonstrating that all Christoffel symbols for a cylindrical surface are zero due to constant metric tensor elements, while spherical and torus surfaces have non-zero symbols derived through detailed examples.
Takeaways
- 📚 Evaluation of Christoffel symbols for sample surface manifolds is illustrated in the video.
- 🔍 Two methods for evaluating Christoffel symbols are discussed.
- 📏 The first method uses basic formulas for Christoffel symbols of the first and second kinds, applying partial derivatives of the covariant metric tensor.
- 📐 For cylindrical surfaces, all elements of the covariant metric tensor are constants, resulting in zero Christoffel symbols.
- 🌐 For spherical surfaces, the only non-zero partial derivative is the partial of s2 with respect to s1, leading to specific non-zero Christoffel symbols.
- 🔄 Christoffel symbols of the first kind for spherical surfaces involve permutations of the values 1, 2, and 2.
- 🔺 The second method uses conversion formulas and the shift tensor, particularly for affine coordinate systems.
- 📉 Christoffel symbols for the torus involve partial derivatives of the metric tensor with respect to surface coordinates.
- 🧩 Contracting with the contravariant metric tensor raises the index to find Christoffel symbols of the second kind.
- 📝 Results for the cylindrical, spherical, and toroidal surfaces are summarized and compared between the two methods.
Q & A
What is the main topic of video 70 in the tensor calculus series?
-The main topic of video 70 is the evaluation of the Christoffel symbols for sample surface manifolds.
How many methods are illustrated in the video to evaluate the Christoffel symbols for surface manifolds?
-Two methods are illustrated in the video to evaluate the Christoffel symbols for surface manifolds.
What is the first method for evaluating the Christoffel symbols as mentioned in the video?
-The first method involves applying basic formulas for the Christoffel symbols of the first kind using the partial derivatives of the covariant metric tensor elements and then contracting those results with the contravariant metric tensor to get the Christoffel symbols of the second kind.
Why are all the Christoffel symbols for the cylindrical surface equal to zero?
-All the Christoffel symbols for the cylindrical surface are equal to zero because all elements of the covariant metric tensor are constants, resulting in all partial derivatives being zero.
What is the only non-zero partial derivative for the spherical surface in the video?
-The only non-zero partial derivative for the spherical surface is ∂s2/∂s1, which is equal to 2a^2 * sin(θ) * cos(θ).
What is the relationship between the Christoffel symbols of the first kind for the spherical surface when the indices are permutations of (1, 2, 2)?
-The Christoffel symbols of the first kind for the spherical surface with indices as permutations of (1, 2, 2) are equal due to the symmetry of the last two indices.
How are the Christoffel symbols of the second kind derived from the first kind for the spherical surface?
-The Christoffel symbols of the second kind for the spherical surface are derived by raising the index, which involves contracting with the contravariant metric tensor.
What is the significance of the ambient coordinate system being an affine coordinate system in the context of the second method for deriving Christoffel symbols?
-If the ambient coordinate system is an affine coordinate system, the Christoffel symbols are all zero, which simplifies the formula for deriving surface Christoffel symbols.
What tensor is used in the second method to derive the Christoffel symbols for the surface?
-The second method uses the shift tensor and its derivatives to derive the Christoffel symbols for the surface.
How does the video demonstrate the use of the second method for deriving the Christoffel symbols for the spherical surface?
-The video demonstrates the use of the second method by showing the calculation of specific Christoffel symbols using the shift tensor, its inverse, and the partial derivatives of the shift tensor elements.
Outlines
📚 Introduction to Christoffel Symbols in Tensor Calculus
This paragraph introduces the topic of evaluating Christoffel symbols for sample surface manifolds in the context of tensor calculus. Two methods are presented for this evaluation, with the first being a direct application of basic formulas involving partial derivatives of the covariant metric tensor. The second method is not detailed in this paragraph. The paragraph also highlights that for a cylindrical surface, the Christoffel symbols are trivially zero due to the constant elements of the metric tensor, leading to all partial derivatives being zero.
🌐 Detailed Calculation of Christoffel Symbols for Spherical Surfaces
The second paragraph delves into the specifics of calculating the Christoffel symbols for a spherical surface. It explains that only one element of the covariant metric tensor is variable, leading to a single non-zero partial derivative. The paragraph outlines the process of finding the non-zero Christoffel symbols of the first kind by considering the permutations of indices. It then describes how to raise the index to obtain the Christoffel symbols of the second kind using the contravariant metric tensor, resulting in specific formulas for the spherical surface.
🦄 Calculation of Christoffel Symbols for Taurine Surfaces Using Partial Derivatives
In this paragraph, the focus shifts to the calculation of Christoffel symbols for a taurian surface. It emphasizes that only one partial derivative is non-zero due to the variable element in the metric tensor being dependent solely on the second surface coordinate. The paragraph details the process of identifying the non-zero Christoffel symbols of the first kind and then raising the index to find the second kind. The contravariant metric tensor's diagonal nature simplifies the calculations, leading to specific results for the taurian surface.
🔍 Alternative Method for Deriving Christoffel Symbols Using Ambient Coordinates
The final paragraph introduces an alternative method for deriving Christoffel symbols by utilizing the ambient coordinate system's properties. It explains that if the ambient system is affine, the Christoffel symbols for the system are zero, simplifying the derivation. The paragraph illustrates this method using the spherical surface as an example, detailing the process of using the shift tensor and its inverse to find the Christoffel symbols. It concludes by showing that the values obtained match those from the first method, thus validating the alternative approach.
Mindmap
Keywords
💡Christoffel Symbol
💡Covariant Metric Tensor
💡Partial Derivatives
💡Cylindrical Surface
💡Spherical Surface
💡Contravariant Metric Tensor
💡Surface Manifolds
💡Shift Tensor
💡Affine Coordinate System
💡Covariant Derivative
Highlights
Introduction of two methods to evaluate the Christoffel symbol for surface manifolds.
Explanation of the first method using basic formulas and partial derivatives of the covariant metric tensor.
Demonstration of the Christoffel symbol calculation for a cylindrical surface resulting in all symbols being zero due to constant tensor elements.
For the spherical surface, identification of the only non-zero partial derivative and its role in determining non-zero Christoffel symbols.
Calculation of Christoffel symbols of the first kind for the spherical surface using specific permutations of indexes.
Raising the index to obtain Christoffel symbols of the second kind by contracting with the contravariant metric tensor.
Derivation of Christoffel symbols for the torus surface with emphasis on the variable element dependent on the second surface coordinate.
Identification of non-zero Christoffel symbols for the torus by considering permutations of indexes 2, 1, and 1.
Calculation of the partial derivative of the shift tensor element with respect to the second surface coordinate for the torus.
Introduction of the second method to calculate Christoffel symbols using conversion formulas and the ambient coordinate system.
Application of the second method to derive Christoffel symbols for the spherical surface using the shift tensor and its inverse.
Illustration of the process to find specific Christoffel symbols using the inverted shift tensor elements and partial derivatives.
Derivation of gamma 1 2 2 using the sum of products of inverted shift tensor elements and their partial derivatives.
Derivation of gamma 2 1 2 showcasing the cancellation of terms and the final result.
Confirmation of the consistency between the two methods by comparing derived values of Christoffel symbols.
Encouragement for viewers to work through other examples on their own to reinforce understanding.
预告下一视频内容,将开始表面协变导数的分析。
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: