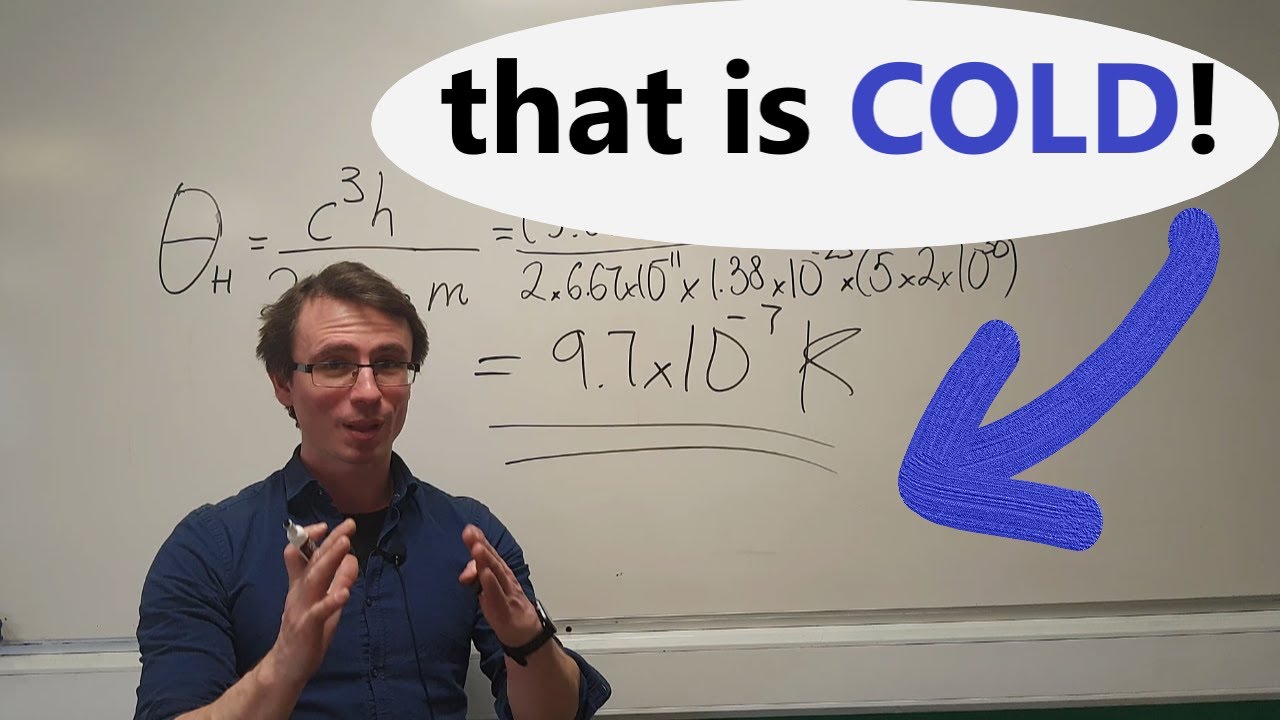Black holes get HOTTER when they LOSE energy?! International Physics Olympiad Solution
TLDRThis video script delves into the peculiar thermodynamics of black holes, contrasting them with normal objects that lose energy as they cool down. It explains that black holes, when losing energy, experience a rise in temperature due to their negative heat capacity, a concept derived from the equations provided. The script guides viewers through the mathematical process of finding the heat capacity of a black hole, emphasizing the negative result which signifies an increase in temperature as energy decreases. The video concludes with an invitation to explore further research on this fascinating and poorly understood aspect of black hole physics.
Takeaways
- 🌡️ When normal objects cool down, they lose energy and temperature.
- 📏 The relationship between energy loss and temperature drop in objects is characterized by heat capacity, denoted as Cv.
- ✏️ Heat capacity is mathematically defined as Cv = dE/dθ, where dE is the change in energy and dθ is the change in temperature.
- 🕳️ Black holes behave differently from normal objects: as they lose energy, their temperature increases.
- ❗ This unusual behavior suggests that black holes have a negative heat capacity.
- 🔍 The script derives the heat capacity of a black hole, starting by examining the relationship between temperature (θ) and mass (M).
- ✒️ The temperature change with respect to mass (dθ/dM) is found to be a function involving fundamental constants like the speed of light, gravitational constant, and Boltzmann's constant.
- 💥 Energy change (dE) in a black hole is related to mass change (dM) through the equation dE = dM * c².
- 🔢 The derived formula for the heat capacity of a black hole is negative, confirming the counterintuitive behavior: C = -2 * G * k * M² / (c³ * h).
- 🤯 The negative heat capacity indicates a rise in temperature as black holes lose energy, a phenomenon not fully understood in quantum statistical mechanics.
Q & A
What happens to the energy of a normal object when it cools down?
-When a normal object cools down, it loses energy. This energy loss is proportional to the change in temperature, with the proportionality constant being the object's heat capacity.
What is the symbol typically used to represent the heat capacity of an object?
-The heat capacity of an object is typically represented by the symbol 'c' with a subscript 'v'.
How does the temperature of a black hole change when it loses energy?
-Unlike normal objects, when a black hole loses energy, its temperature actually rises, indicating a unique thermodynamic behavior.
What is the relationship between the heat capacity and the temperature change of a black hole?
-The heat capacity of a black hole is negative, which means that as it loses energy, its temperature increases.
What is the mathematical expression for the heat capacity of a black hole?
-The heat capacity of a black hole is given by the negative expression: -2 * gravitational constant * Boltzmann's constant * mass squared / (speed of light squared * Planck's constant).
What is the significance of a negative heat capacity in the context of black holes?
-A negative heat capacity signifies that black holes have an inverse relationship between energy loss and temperature change, which is a counterintuitive and complex phenomenon in thermodynamics.
Why is the temperature of a black hole considered when discussing its heat capacity?
-The temperature of a black hole is considered because it is directly related to the energy it emits, and understanding this relationship helps in studying its thermodynamic properties.
What is the role of Boltzmann's constant in the context of black hole heat capacity?
-Boltzmann's constant is a fundamental constant in physics that relates the energy at the quantum level to temperature. In the context of black holes, it is used in the formula to calculate the negative heat capacity.
How does the mass of a black hole affect its heat capacity?
-The mass of a black hole is a key factor in its heat capacity. As indicated in the formula, the heat capacity is inversely proportional to the square of the black hole's mass.
What is the current understanding of the quantum statistical processes in black holes?
-The current understanding of the quantum statistical processes in black holes is limited. The script mentions that there is no good model for how these processes occur at a fundamental level.
What resources are available for further exploration of black hole physics as presented in the script?
-The script mentions that there are research papers and derivations available for further exploration, which are linked in the description of the video.
Outlines
🌡️ Understanding Heat Capacity and Energy Loss in Objects
This section explains how normal objects lose energy when they cool down, resulting in a decrease in temperature, denoted as Δθ. The relationship between the lost energy (ΔE) and the temperature change is defined by the object's heat capacity, symbolized as Cv. The heat capacity is derived as the ratio of ΔE to Δθ, leading to the expression dE/dθ. This forms the basis for understanding how heat capacity functions in typical physical systems.
🕳️ Black Holes and Their Mysterious Heat Capacity
Unlike normal objects, black holes behave counterintuitively when they lose energy; their temperature actually increases. This implies that black holes have a negative heat capacity. The video intends to calculate the heat capacity of a black hole using specific equations, which are derived in previous videos on the channel. The focus is on understanding the implications of a negative heat capacity in black holes.
📉 Calculating dθ: The Temperature-Mass Relationship in Black Holes
The video proceeds to analyze the change in temperature (dθ) as a function of the black hole's mass (M). By differentiating the temperature equation with respect to mass, the video derives an expression for dθ, emphasizing the importance of the negative sign in the equation. This negative sign is crucial for the overall calculation of the black hole's heat capacity.
⚡ Calculating dE: Energy Loss in Black Holes
Next, the focus shifts to calculating the infinitesimal energy change (dE) in a black hole due to a small mass change (dM). The famous equation E=mc² is used to express this energy change. The video then substitutes this expression into the equation for heat capacity, setting the stage for the final calculation.
🔄 Final Heat Capacity Formula for Black Holes
In this section, the derived expressions for dE and dθ are combined to form the final equation for the heat capacity of a black hole. The resulting expression is negative, confirming the counterintuitive behavior where a black hole's temperature rises as it loses energy. This calculation reveals a deeper mystery in black hole physics, challenging our understanding of thermodynamics in extreme environments.
❓ The Unresolved Mystery of Black Hole Heat Capacity
The video concludes by reflecting on the implications of the negative heat capacity of black holes. Despite deriving the mathematical expression, the physical mechanisms behind this phenomenon remain poorly understood. The video encourages viewers to explore linked research papers for further insights and acknowledges the complexity and mystery still surrounding black hole thermodynamics.
Mindmap
Keywords
💡Heat Capacity
💡Black Hole
💡Negative Heat Capacity
💡Energy (ΔE)
💡Temperature (Δθ)
💡Boltzmann's Constant (kB)
💡Mass (m)
💡Planck's Constant (h)
💡Gravitational Constant (G)
💡Hawking Radiation
Highlights
Normal objects lose energy and their temperature decreases when cooled down.
The heat capacity of an object is the coefficient between lost energy and temperature change, symbolized as \( c_v \).
Black holes behave differently; as they lose energy, their temperature rises, implying a negative heat capacity.
The heat capacity of a black hole can be derived using differential equations.
The temperature of a black hole is a function of its mass, and its infinitesimal change can be found by differentiation.
The derivative of the temperature with respect to mass is proportional to \( \frac{-k_B T}{m^2} \), where \( k_B \) is Boltzmann's constant.
The infinitesimal energy loss of a black hole is related to its mass loss by the equation \( dE = dm c^2 \).
The heat capacity of a black hole is expressed as the ratio of the infinitesimal energy loss to the infinitesimal temperature change.
The calculation results in a negative heat capacity for black holes, indicating a temperature increase as they lose energy.
The negative heat capacity formula for a black hole involves the gravitational constant, Boltzmann's constant, mass, speed of light, and Planck's constant.
The phenomenon of black holes heating up as they lose energy is not well understood and lacks a clear statistical quantum model.
Research papers on the subject have been reviewed and are available for those interested in the quantum mechanics of black holes.
The video aims to provide an appreciation of the unusual aspects of black hole physics.
The video concludes with an invitation to the next episode, suggesting a series on the topic.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: