HAWKING Radiation Physics Olympiad Problem

ZPhysics
28 Jan 202206:39
EducationalLearning
32 Likes 10 Comments

TLDRThis script from a physics education video explores the concept of black hole temperature and its implications for black hole evaporation through Hawking radiation. It derives the power emitted by a black hole using Stefan-Boltzmann's law and relates this to the rate of energy loss. The script then translates this energy loss into a differential equation for the mass loss of a black hole, highlighting the famous equation E = mc^2 to connect energy loss with mass loss. The video encourages viewers to visit Just Calculus's channel for the solution to this differential equation and to learn about the evaporation time of black holes.

Takeaways
  • 🌀 Black holes have a temperature, meaning they radiate energy.
  • 📚 The video is part of a 2007 International Physics Olympiad problem discussing the Hawking temperature of black holes.
  • 🔬 Dimensional analysis helps derive the expression for sigma (a constant) and the area of the event horizon of a black hole.
  • 💥 The video aims to explore how the loss of energy over time affects the mass of a black hole, focusing on deriving a differential equation for this mass loss.
  • 📊 The Stefan-Boltzmann law is used to calculate the power emitted by a black hole based on its temperature.
  • 🔗 Substituting various expressions leads to the rate of change of energy of the black hole, using constants like Boltzmann's constant, speed of light, and gravitational constant.
  • 🧮 Simplifications and cancellations of terms lead to a formula that expresses the rate of change of mass in relation to energy loss via Hawking radiation.
  • 📉 The derived differential equation shows how much mass a black hole loses per second.
  • 🔍 The equation dE = dM * c^2 is used to relate energy loss to mass loss, leading to a simplified differential equation.
  • 🔗 The video encourages viewers to visit the Just Calculus channel for a detailed solution of the differential equation and to learn about the evaporation time of black holes.
Q & A

  • What does it mean when black holes have a temperature?

    -When black holes have a temperature, it implies that they radiate energy, a phenomenon known as Hawking radiation. This concept contradicts the classical idea that nothing can escape a black hole.

  • What was derived in the first part of the 2007 International Physics Olympiad problem mentioned in the script?

    -In the first part of the problem, an expression for the Hawking temperature of a black hole was derived, and dimensional analysis was used to find expressions for constants like sigma and the area of the event horizon.

  • How does the loss of energy affect the mass of a black hole?

    -The loss of energy due to Hawking radiation leads to a decrease in the mass of the black hole over time. The script explores how this mass loss can be quantified using a differential equation.

  • What equation is used to relate the rate of energy loss to the mass loss of a black hole?

    -The rate of energy loss is related to mass loss using the equation dE/dt = -dM/dt * c^2, which is a differential form of Einstein's equation E = mc^2.

  • What is the significance of Stefan-Boltzmann's law in the context of black hole radiation?

    -Stefan-Boltzmann's law is used to calculate the power emitted by a black hole due to its temperature. By substituting the Hawking temperature into this law, one can derive the rate at which a black hole radiates energy.

  • How are constants like the speed of light (c), Planck's constant (h), and the gravitational constant (G) used in the equation?

    -These constants are used to form the expression for the rate of energy loss. The script details the process of combining these constants to arrive at the final equation for dE/dt.

  • What happens to the terms involving the Boltzmann constant (kb) during the derivation?

    -The terms involving the Boltzmann constant (kb) are canceled out during the simplification of the equation for the rate of energy loss.

  • How is the final differential equation for mass loss derived?

    -The final differential equation for mass loss is derived by substituting the expression for energy loss into the differential form of Einstein's equation. Further simplifications and cancellations lead to the final form of the equation.

  • What does the final differential equation tell us about black hole evaporation?

    -The final differential equation describes how the mass of a black hole decreases over time due to Hawking radiation. It provides a way to calculate the evaporation time of a black hole.

  • Where can one find the solution to the differential equation mentioned in the script?

    -The solution to the differential equation can be found on the 'Just Calculus' channel, which is recommended in the script for further exploration and learning.

Outlines
00:00
🌌 Understanding Black Hole Radiation and Energy Loss

This paragraph delves into the concept of black holes having a temperature and radiating energy, as explored in a 2007 International Physics Olympiad problem. It discusses deriving the Hawking temperature for a black hole and using dimensional analysis to find expressions for constants and the area of the event horizon. The main focus is on understanding how the loss of energy over time affects the black hole's mass and finding a differential equation for this mass loss. The paragraph concludes with a reference to a calculus channel for solving the derived equation and learning more about the subject.

05:02
🔢 Deriving the Differential Equation for Mass Loss in Black Holes

The second paragraph continues the discussion on black holes by applying the Stefan-Boltzmann law to calculate the power radiated by a black hole with a given temperature. It then substitutes expressions derived earlier to find the rate of change of energy. The process involves significant cancellation of terms, leading to a simplified expression for the rate of energy change over time. The paragraph introduces the famous equation E = mc^2 to relate energy loss to mass loss, resulting in a differential equation for the rate of mass change due to Hawking radiation. It ends with an invitation to a calculus channel for solving this equation and determining the evaporation time of a black hole.

Mindmap
Keywords
💡Black Hole
A black hole is a region of space where gravity is so strong that nothing, not even light, can escape from it. In the video, the black hole is central to the discussion, particularly in understanding how it radiates energy and loses mass over time through Hawking radiation.
💡Hawking Radiation
Hawking radiation is theoretical radiation that is predicted to be emitted by black holes due to quantum effects near the event horizon. The video focuses on the derivation of the Hawking temperature, which plays a crucial role in understanding the energy loss and mass reduction of black holes.
💡Event Horizon
The event horizon is the boundary surrounding a black hole, beyond which nothing can return. In the video, the event horizon is mentioned as the area 'A' that is crucial in the calculations involving black hole radiation and the Hawking temperature.
💡Stefan-Boltzmann Law
The Stefan-Boltzmann Law relates the power radiated by an object to its temperature. The video applies this law to black holes to derive the rate of energy loss, which is directly linked to the decrease in the black hole’s mass over time.
💡Differential Equation
A differential equation is a mathematical equation that relates a function to its derivatives, representing how a quantity changes over time. In the video, a differential equation is derived to describe the rate at which a black hole loses mass due to Hawking radiation.
💡Dimensional Analysis
Dimensional analysis is a technique used to understand the relationships between physical quantities by considering their units. The video references this method as a way to derive expressions for constants like 'sigma' and to validate the expression for the Hawking temperature.
💡Boltzmann's Constant (kb)
Boltzmann's constant is a fundamental physical constant that relates the average kinetic energy of particles in a gas with the temperature of the gas. In the video, it appears in the formula for the Hawking temperature and plays a role in calculating the energy radiated by the black hole.
💡Gravitational Constant (G)
The gravitational constant is a fundamental constant that appears in Newton's law of universal gravitation. It is crucial in calculating gravitational forces and in the video, it is used in the formulas for the energy and temperature of the black hole, impacting the rate of mass loss.
💡Planck's Constant (h)
Planck's constant is a fundamental constant that relates the energy of a photon to its frequency. In the video, Planck's constant appears in the expression for the power radiated by the black hole, contributing to the calculation of how energy is emitted.
💡Mass-Energy Equivalence (E=mc^2)
Mass-energy equivalence is the principle that energy and mass are interchangeable, as expressed in Einstein's equation E=mc^2. The video uses a differential form of this equation (dE = dmc^2) to link the loss of mass in a black hole to the energy it radiates away via Hawking radiation.
Highlights

Black holes have a temperature, which means they radiate energy.

The video is part of a 2007 International Physics Olympiad problem, focused on deriving an expression for the Hawking temperature of a black hole.

Dimensional analysis helped find an expression for sigma, a constant, and the area A of the event horizon of the black hole.

The video explores how the loss of energy over time affects the mass of the black hole.

A differential equation for the loss of mass of the black hole is derived.

Stefan-Boltzmann's law is used to calculate the power emitted by the black hole.

The power is calculated by substituting expressions derived earlier in the problem.

Cancellation of terms in the equation simplifies the expression for the rate of change of energy of the black hole.

The famous equation E = mc^2 is applied to find the rate of change of mass due to energy loss.

The resulting differential equation describes how much mass the black hole loses per second.

The final equation shows the rate of change of mass of a black hole via Hawking radiation.

Viewers are encouraged to check out the 'Just Calculus' channel for solving the differential equation.

The differential equation can be used to find the evaporation time of a black hole.

The process highlights the intricate relationship between energy, mass, and radiation in black holes.

The collaboration between channels emphasizes the educational value of the content in learning complex physics and calculus concepts.

Transcripts

Browse More Related Video

Deriving Hawking's most famous equation: What is the temperature of a black hole?

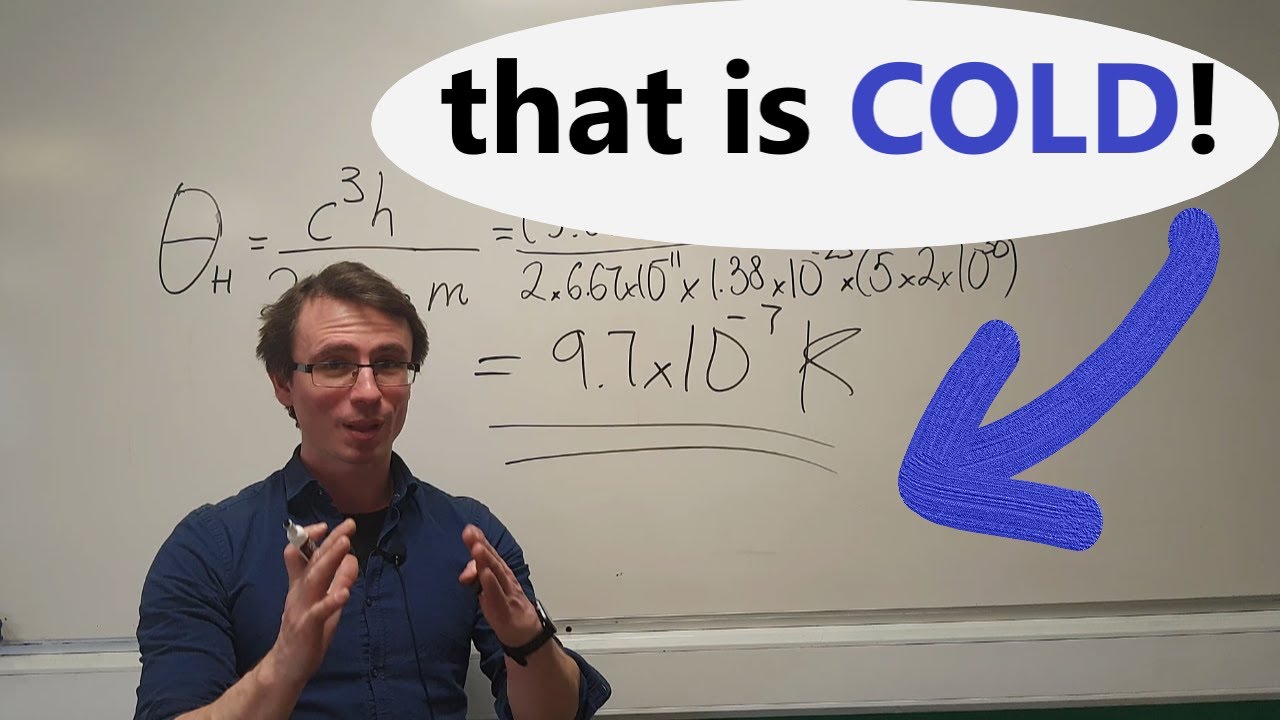
What is the Hawking temperature of a black hole? IPhO Problem

My solutions to the International Physics Olympiad: The Physics of Black Holes, IPhO Iran 2007

How to Make Black Holes (Both Regular and Supermassive)

Black holes get HOTTER when they LOSE energy?! International Physics Olympiad Solution

LAST Problem from the International Physics Olympiad

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Black HolesHawking RadiationPhysicsEvaporationMass LossStefan-BoltzmannDifferential EquationsCalculusRadiation PowerSpace-TimeAstrophysics