Statistical Process Control | Chart for Means (x-bar chart)

Joshua Emmanuel
21 Jul 201503:46
EducationalLearning
32 Likes 10 Comments

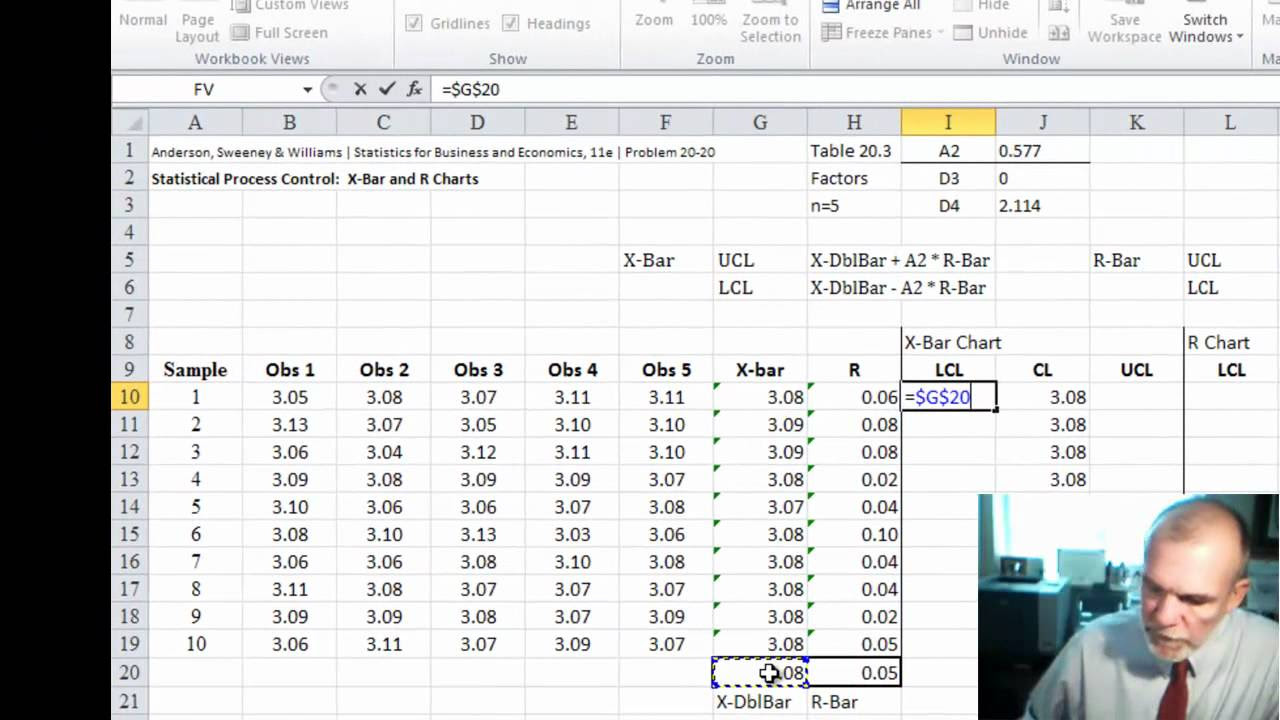
TLDRThis tutorial introduces constructing an x-bar control chart to determine if a process is in statistical control. It explains calculating the centerline and control limits using sample means, ranges, and R-bar, along with the A2 factor from a control chart factors table. The process data involves 10 days of samples, each of size 5. The chart reveals the process is out of control on day 5, suggesting a need for investigation and corrective actions.

Takeaways
  • 📊 The tutorial is about constructing an x-bar control chart to determine if a process is in statistical control.
  • 📈 A control chart includes a centerline, upper control limit (UCL), and lower control limit (LCL).
  • 🧩 The centerline of the x-bar chart is represented by the mean of the sample means, denoted as x-double bar.
  • 🔢 The control limits are calculated using the range of the process, with the UCL being x-double bar plus A2 times R-bar, and the LCL being x-double bar minus A2 times R-bar.
  • 📐 R-bar is the average of the sample ranges, which is calculated by summing all ranges and dividing by the number of samples.
  • 🔍 A2 is a control chart factor found in a control chart factors table, specific to the sample size.
  • 🗓️ The process data used in the tutorial consists of samples of size 5 collected daily for 10 days.
  • 📝 The range for each sample is the difference between the largest and smallest values, and the mean is calculated by summing and dividing by the sample size.
  • 🔑 To find A2, refer to the control chart factors table for the corresponding value based on the sample size.
  • 📉 The x-bar chart is completed by plotting the sample points, drawing the control limits, and creating a run chart.
  • 🚫 If a sample mean falls outside the control limits, such as below the LCL, it indicates the process is out of control and requires investigation.
Q & A

  • What is the purpose of a control chart for x-bar?

    -The purpose of a control chart for x-bar is to construct a chart from process data to determine if the process mean is in statistical control.

  • What are the three components of a control chart?

    -The three components of a control chart are the centerline, the lower control limit (LCL), and the upper control limit (UCL).

  • What does the centerline of an x-bar chart represent?

    -The centerline of an x-bar chart represents the mean of the sample means, denoted as x-double bar.

  • If the standard deviation of the process is known, what formula is used to calculate the control limits?

    -If the standard deviation of the process is known, a specific formula is used to calculate the control limits, but in the provided script, the range is used instead.

  • What is the formula for calculating the upper control limit (UCL) of an x-bar chart when using the range?

    -The formula for calculating the UCL when using the range is UCL = x-double bar + A2 * R-bar.

  • What is R-bar and how is it calculated?

    -R-bar is the average of the sample ranges. It is calculated by summing all the ranges and dividing by the number of samples.

  • What is A2 and where can it be found?

    -A2 is a control chart factor used in calculating the control limits. It can be found in the control chart factors table corresponding to the sample size.

  • How is the sample range calculated?

    -The sample range is calculated by subtracting the smallest value in the sample from the largest value.

  • What does it mean if a sample mean falls outside the control limits?

    -If a sample mean falls outside the control limits, it indicates that the process mean is not in statistical control, or is out of control.

  • What action is recommended when the process is found to be out of control?

    -When the process is found to be out of control, it is recommended to investigate the activities of the day when the out-of-control condition occurred to determine the special cause of variation and to take necessary corrective actions.

  • How can the control chart help in identifying special causes of variation?

    -The control chart helps in identifying special causes of variation by showing when the process mean falls outside the control limits, signaling a potential non-random variation that requires investigation.

Outlines
00:00
📊 Introduction to x-bar Control Chart

This paragraph introduces the concept of the x-bar control chart, a statistical tool used to determine if a process is in statistical control. It explains the components of the chart, including the centerline, upper control limit (UCL), and lower control limit (LCL), and mentions the use of the sample mean (x-double bar) and range in calculating these limits. The video script outlines the process of constructing an x-bar chart using process data collected over 10 days with sample sizes of 5, aiming to assess whether the process mean is stable and predictable.

Mindmap
Keywords
💡Control chart
A control chart is a statistical tool used to determine whether a process is in a state of statistical control. It consists of a centerline, an upper control limit (UCL), and a lower control limit (LCL). In the video, the x-bar chart is a specific type of control chart used to monitor the process mean over time, and it is constructed using the process data provided.
💡x-bar chart
The x-bar chart is a type of control chart that is used to monitor the mean of a process when the samples are of constant size. It is named after the use of the sample mean (x-bar) as the central measure. In the script, the x-bar chart is being constructed to analyze the process data and determine if the process mean is in statistical control.
💡Statistical control
Statistical control refers to a state where a process is only affected by common causes of variation and not by any special causes. A process in statistical control is predictable and stable. In the video, the determination of whether the process is in statistical control is the main objective, and it is concluded that the process is out of control when a sample mean falls outside the control limits.
💡Centerline
The centerline of a control chart represents the average value of the process being monitored. For an x-bar chart, the centerline is the mean of all sample means, denoted as x-double bar in the script. It serves as a reference point to compare the stability of the process over time.
💡Upper control limit (UCL)
The upper control limit is a value on the control chart above the centerline that defines the upper boundary of expected natural variation in the process. In the script, the UCL for the x-bar chart is calculated using the formula UCL = x-double bar + A2 * R-bar, where A2 is a control chart factor and R-bar is the average range of the samples.
💡Lower control limit (LCL)
The lower control limit is the value on the control chart below the centerline that defines the lower boundary of expected natural variation. In the context of the video, the LCL is calculated using the formula LCL = x-double bar - A2 * R-bar, which helps in identifying if the process mean has deviated from the expected range.
💡Sample size
Sample size refers to the number of observations or data points in each sample taken from the process. In the script, the sample size is consistently 5, meaning each sample consists of five observations that are used to calculate the mean and range for the x-bar chart.
💡Range
The range is a measure of dispersion that represents the difference between the maximum and minimum values in a sample. In the video, the range is calculated for each sample to determine the variability within that sample, which is then used to calculate R-bar and the control limits.
💡R-bar
R-bar is the average of the ranges of all samples. It is used in the calculation of the control limits for the x-bar chart. In the script, R-bar is calculated by summing all the sample ranges and dividing by the number of samples, which in this case is 10.
💡x-double bar
x-double bar represents the mean of the sample means, which serves as the centerline of the x-bar chart. It is calculated by summing all the sample means and dividing by the number of samples. In the script, x-double bar is determined to be 497.8 after summing and averaging the means of the 10 samples.
💡A2
A2 is a control chart factor used in the calculation of the control limits for an x-bar chart when the sample size is known. It is derived from a control chart factors table based on the sample size. In the video, A2 is found to be 0.577 for a sample size of 5, and it is used in the formulas for UCL and LCL.
💡Special cause
A special cause is an unusual or non-random event that causes a process to deviate from its expected performance. In the script, when the sample mean for day 5 falls below the LCL, it indicates a potential special cause that is causing the process to be out of control, prompting an investigation into the activities of that day.
Highlights

Introduction to constructing an x-bar chart for statistical process control.

Explanation of the components of a control chart: centerline, upper control limit (UCL), and lower control limit (LCL).

The centerline of the x-bar chart is the mean of the sample means (x-double bar).

Use of the range to calculate control limits when the process standard deviation is unknown.

Formula for calculating UCL and LCL using x-double bar, A2, and R-bar.

R-bar is the average of the sample ranges.

A2 value is obtained from the control chart factors table based on sample size.

Process data consists of samples of size 5 collected daily for 10 days.

Objective to determine if the process mean is in statistical control.

Method for obtaining sample ranges and means.

Calculation of R-bar and x-double bar from the sum of ranges and means.

Determination of A2 value for a sample size of 5 from the control chart factors table.

Calculation of UCL and LCL using the determined values of A2, x-double bar, and R-bar.

Construction of the x-bar chart with sample points, control limits, and a run chart.

Identification of a process out of statistical control due to a sample mean below the LCL.

Recommendation to investigate the activities of day 5 for special causes of variation.

Conclusion and summary of the x-bar chart process.

Transcripts

Browse More Related Video

CONTROL CHART BASICS and the X-BAR AND R CHART +++++ EXAMPLE

XBar-R Control Charts

Create a Basic Control Chart

Statistical Process Control | SPC Control charts (IMR ) using Minitab 17 |

Making a Control Chart in Excel (with dynamic control lines!)

Attribute Data Control Chart Examples!! How to select/create the P, NP, C and U Charts

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Statistical ControlProcess DataControl Chartx-bar ChartQuality ControlSample MeansControl LimitsProcess AnalysisData InterpretationContinuous ImprovementSpecial Causes