Residual plots | Exploring bivariate numerical data | AP Statistics | Khan Academy

Khan Academy
11 Jul 201706:12
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the concept of a residual plot in the context of regression analysis. It explains that residuals represent the difference between actual and expected values. The script illustrates how to calculate and plot residuals for a simple least squares regression, emphasizing their importance in assessing the fit of the model. A good fit is indicated by residuals that are randomly scattered, while a trend in the residuals suggests a poor fit and the potential need for a non-linear model. The script uses examples to highlight how residual plots can guide the choice of an appropriate regression model.

Takeaways
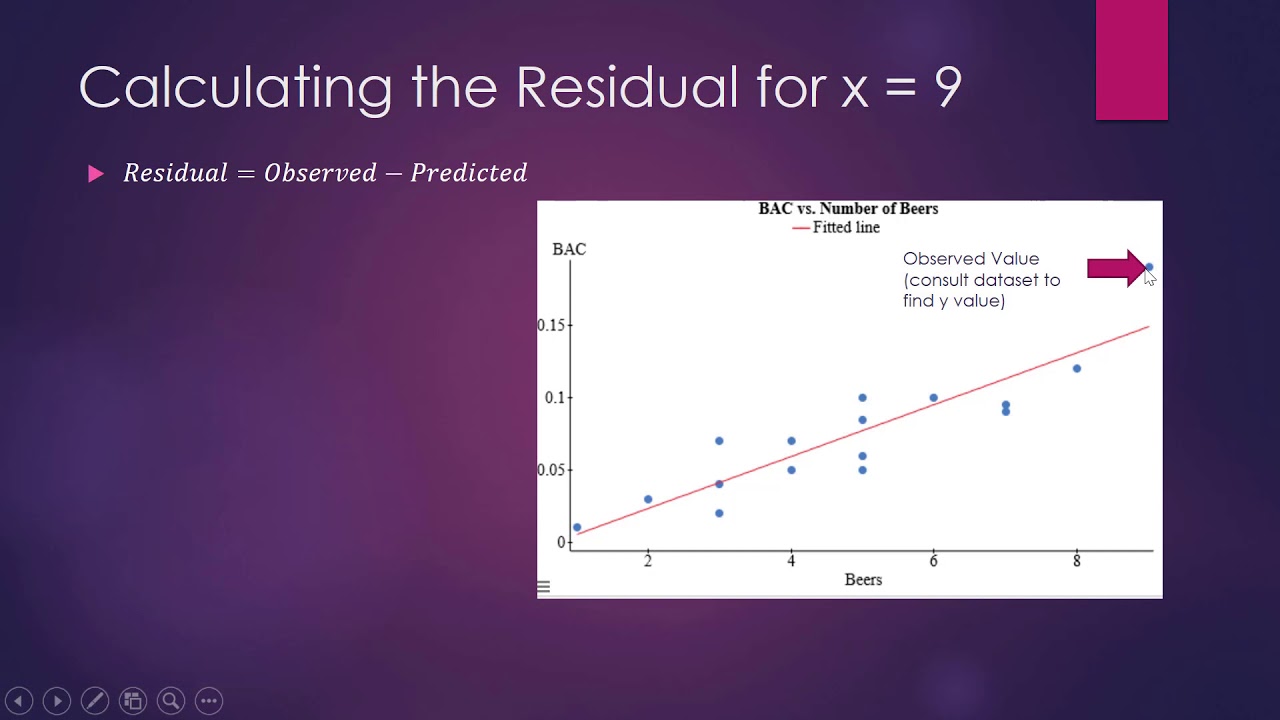
  • 📈 A residual plot is used to evaluate the fit of a regression line to data points.
  • 🔍 Residuals are calculated as the difference between the actual and expected values for a given point.
  • 🤔 A positive residual indicates that the actual value is above the regression line, while a negative residual indicates it is below.
  • 📊 Plotting residuals involves setting up axes based on the x-values of the data points and marking the residuals above or below a baseline.
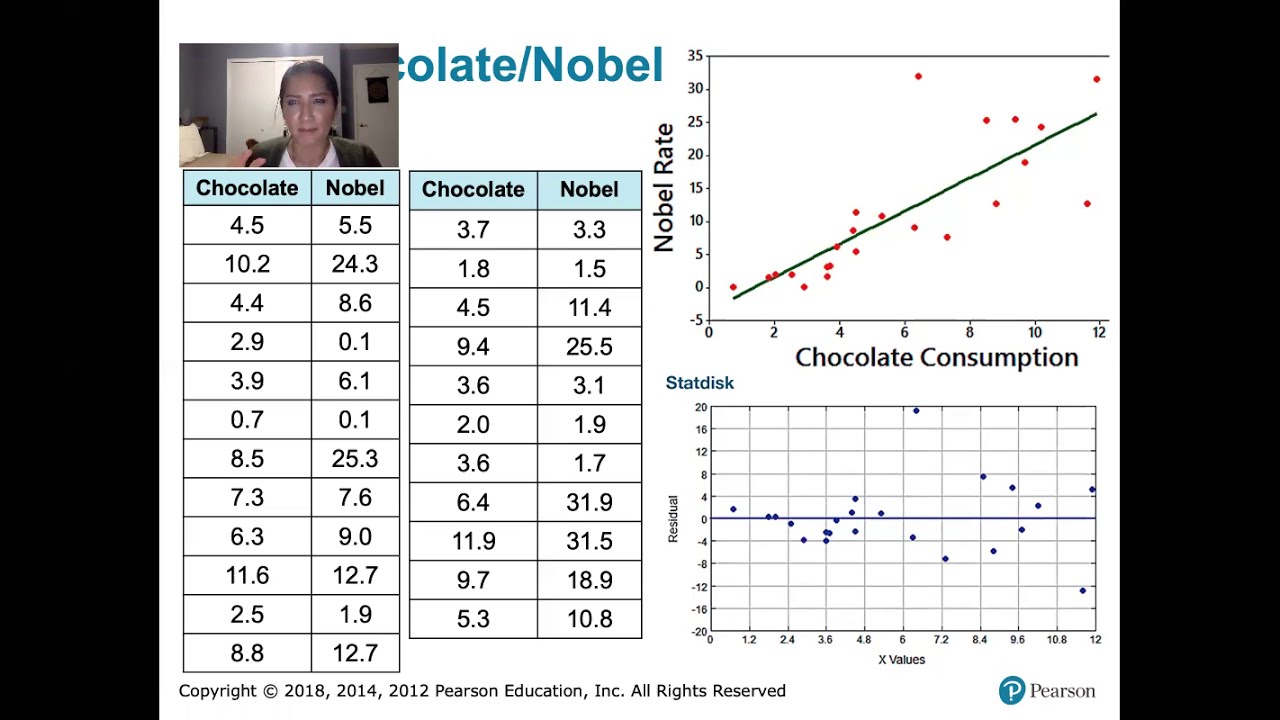
  • 🎯 The goal of a residual plot is to determine if the residuals are randomly scattered, which would suggest a good fit from the regression line.
  • 📈 If a trend is observed in the residual plot, such as an upward or downward trend, it may indicate that a non-linear model is more appropriate.
  • 🔢 Large residuals far from the x-axis can also indicate a poor fit of the regression line to the data.
  • 📊 An example in the script shows a linear model with evenly scattered residuals, suggesting a good fit.
  • 🔍 A different residual plot with a trend of going down and then up indicates a potential non-linear relationship between the variables.
  • 📈 The R value, while positive, is not close to one, indicating that the model may not be the best fit for the data.
  • 💡 Analyzing residual plots helps in deciding whether to stick with a linear model or to explore non-linear alternatives for better data fit.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is the concept and analysis of a residual plot in the context of regression analysis.

  • What is a residual in the context of regression?

    -A residual is the difference between the actual observed value and the expected value predicted by the regression line for a given point.

  • How do you calculate the residual for a point on the regression line?

    -You calculate the residual by subtracting the expected value (predicted by the regression line) from the actual observed value for a specific point.

  • What does a positive residual indicate?

    -A positive residual indicates that the actual observed value is greater than the expected value predicted by the regression line.

  • What does a negative residual indicate?

    -A negative residual indicates that the actual observed value is less than the expected value predicted by the regression line.

  • How is a residual plot constructed?

    -A residual plot is constructed by plotting the residuals on the y-axis and the x-values of the data points on the x-axis. Each point on the plot represents the residual for a specific x-value.

  • Why are residual plots useful in regression analysis?

    -Residual plots are useful because they help to assess the quality of the fit of the regression line. They can reveal trends or patterns in the residuals that might suggest a poor fit or the need for a non-linear model.

  • What does a random scattering of points in a residual plot suggest about the regression line?

    -A random scattering of points in a residual plot suggests that the regression line is a good fit for the data, as there is no discernible pattern or trend in the residuals.

  • What type of trend in a residual plot might indicate a poor fit for the regression line?

    -An upward or downward trend, or a pattern of curving up and then down in a residual plot, might indicate that the regression line is not a good fit for the data and that a non-linear model could be more appropriate.

  • How can the R value be related to the pattern observed in a residual plot?

    -The R value, which measures the strength of the linear relationship between the variables, can be related to the pattern in a residual plot. A low R value, especially if combined with a clear pattern in the residuals, might indicate that the regression line is not a good fit for the data.

  • What does a large number of residuals far from the x-axis in a residual plot suggest?

    -A large number of residuals far from the x-axis in a residual plot suggests that the regression line may not be a good fit for the data, as it indicates that many predicted values deviate significantly from the actual observed values.

Outlines
00:00
📊 Introduction to Residual Plots

This paragraph introduces the concept of a residual plot in the context of regression analysis. The instructor explains that a residual plot is used to visualize the differences (residuals) between the actual data points and the values predicted by a regression line. The explanation includes a step-by-step process of calculating residuals for given data points and plotting them on a graph. The purpose of a residual plot is to assess the quality of the fit of the regression line to the data. If the residuals appear to be randomly scattered without any discernible pattern, it suggests that the regression line is a good fit. However, if there is a noticeable trend in the residuals, it indicates that the line may not be a suitable model for the data, potentially necessitating a non-linear model.

05:02
📈 Evaluating Fit with Residual Plots

In this paragraph, the instructor further elaborates on the use of residual plots to evaluate the fit of a linear model. The discussion includes examples of how to interpret the plots. If the residuals are evenly scattered above and below the line, it suggests that the linear model is a good fit for the data. Conversely, if the residual plot shows a trend, such as a pattern of increase or decrease, or if there are many residuals far from the x-axis, it indicates that the linear model may not be appropriate. The instructor also mentions the R value, a statistical measure of how well the observed data fit a model, and suggests that a low R value in conjunction with a non-random residual plot would indicate a poor fit for the linear model.

Mindmap
Keywords
💡residual plot
A residual plot is a graphical representation that displays the differences, or residuals, between the actual observed values and the expected values predicted by a regression model. In the context of the video, residual plots are used to assess the quality of fit of a regression line by visualizing how closely the data points align with the model's predictions. A random scattering of residuals indicates a good fit, while a pattern suggests that the model may not adequately capture the relationship between the variables.
💡regression
Regression is a statistical method used to analyze the relationship between two or more variables, where one variable is considered the dependent variable and the others are independent. In the video, the focus is on least squares regression, a common type of linear regression that aims to find the line of best fit through a set of data points by minimizing the sum of the squares of the residuals. The concept is central to understanding how well the model explains the data and the creation of residual plots.
💡least squares
Least squares is a mathematical approach to fitting a regression line to a set of data points. It operates by minimizing the sum of the squares of the vertical distances (residuals) between the observed values and the values predicted by the model. In the video, the least squares method is used to derive the equation of the regression line, which is then compared to the actual data points to calculate residuals and create a residual plot.
💡residual
A residual is the difference between an observed value and the value predicted by a model or equation. In the video, residuals are calculated for each data point based on the actual y-values and the expected y-values from the least squares regression line. The sign and magnitude of the residuals provide insights into how well the model fits the data, with a positive residual indicating an overestimation and a negative residual indicating an underestimation.
💡fit
In the context of the video, 'fit' refers to how well a statistical model, such as a regression line, aligns with the observed data. A good fit indicates that the model accurately captures the relationship between the variables, while a poor fit suggests that the model may not adequately represent the data. The residual plot is a tool used to visually assess the quality of the fit by examining the distribution of residuals.
💡scatter
In the context of the video, 'scatter' refers to the visual distribution of data points on a plot. When residuals are scattered evenly and randomly above and below the line in a residual plot, it suggests that the regression model is a good fit for the data. Conversely, if the residuals show a pattern or trend, such as clustering or a curve, it indicates that the model may not be capturing the true relationship between the variables.
💡non-linear model
A non-linear model is a type of statistical model that does not assume a straight-line relationship between variables. In the video, if the residual plot shows a pattern or trend that suggests the data is not well-fit by a linear regression line, a non-linear model may be considered as an alternative. Non-linear models can capture more complex relationships, such as curves or exponential growth, providing a better fit to the data.
💡actual vs expected
In the context of the video, 'actual' refers to the real, observed values of the dependent variable, while 'expected' refers to the values predicted by the regression model. The comparison between actual and expected values is crucial for calculating residuals and assessing the accuracy of the model. The goal is to minimize the difference between the actual and expected values, which is reflected in the residuals.
💡R value
The R value, or R-squared, is a statistical measure that represents the proportion of the variance for the dependent variable that's explained by the independent variables in a regression model. In the video, an R value close to one indicates a strong correlation and a good fit of the model to the data, while a lower R value suggests a weaker relationship. The R value is used to evaluate the overall effectiveness of the regression model.
💡x-axis and y-axis
The x-axis and y-axis are the horizontal and vertical axes, respectively, on a two-dimensional coordinate system used for plotting data points and creating graphs. In the video, the x-axis represents the independent variable (e.g., x), and the y-axis represents the dependent variable (e.g., y). The residual plot is created on this coordinate system, with the x-axis representing the predicted values and the y-axis representing the residuals.
💡trend
A trend in the context of the video refers to a pattern or direction that emerges when observing data points over time or across different values of an independent variable. In a residual plot, a trend can indicate that the regression model is not capturing the true nature of the relationship between the variables. For example, if residuals increase or decrease consistently as the predicted values increase, this upward or downward trend suggests that a more complex model may be needed to better fit the data.
Highlights

The video discusses the concept of a residual plot in the context of regression analysis.

A residual plot is used to visualize the difference between the actual and expected values from a regression line.

The residual for a point is calculated as the actual value minus the expected value.

A positive residual indicates that the actual value is above the regression line.

A negative residual indicates that the actual value is below the regression line.

A residual plot can help determine the quality of fit of a regression line to the data.

Randomly scattered residuals around the horizontal axis suggest a good fit of the regression line.

Systematic trends in the residual plot, such as a curve, indicate a poor fit for the linear model.

A non-linear model may be more appropriate if the residual plot shows a discernible trend.

Large residuals far from the x-axis in the residual plot also suggest a poor fit of the model.

The R value can be used to quantify the goodness of fit, with values closer to one indicating a better fit.

The example provided in the video demonstrates how to plot residuals for a given set of data points.

The video explains how to interpret a residual plot and what it indicates about the regression model's fit.

The video provides a clear and detailed explanation of the concept of residuals and their importance in regression analysis.

The video uses a step-by-step approach to illustrate how to calculate and plot residuals for a set of data points.

The video emphasizes the practical application of residual plots in assessing the suitability of a linear model for a given dataset.

The video's content is relevant for anyone looking to understand and apply regression analysis techniques.

Transcripts

Browse More Related Video

interpreting residual graphs

Residuals and Residual Plots

Calculating Residuals & Making Residual Plots on TI-84 Plus

How to Calculate the Residual

10.2.6 Regression - Residual Plots and Their Interpretation

RESIDUALS! What are they? how to find them, how to use them

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Regression AnalysisResidual PlotsModel EvaluationData FittingStatistical TrendsLinear vs Non-LinearData AnalysisMachine LearningPredictive ModelingStatistical Interpretation