Calculus Chapter 3 Lecture 21 Substitution
TLDRIn this calculus lecture, Professor Greist introduces the concept of substitution, a fundamental method for computing integrals, derived from differentiation rules. Through examples, he demonstrates how to simplify complex integrals by converting them into simpler forms using u-substitution. He also applies these techniques to solve a differential equation modeling tumor growth, revealing the equilibrium points and the behavior of the solution. The lecture emphasizes the importance of understanding substitution as a change of variables, a concept crucial for tackling more complex integrals in multivariable calculus.
Takeaways
- 📚 The lecture introduces the concept of substitution as a method for computing integrals, emphasizing its connection to differentiation rules.
- 🔍 The linearity of integration is highlighted, showing that the integral of a sum is the sum of integrals and that constants can be factored out of integrals.
- 🔄 The u-substitution formula is derived from the chain rule, allowing for the simplification of complex integrals by transforming them into simpler forms.
- 🌰 An example is provided where the integral of \( e^{\sin(x)} \cos(x) \, dx \) is simplified using u-substitution, resulting in \( e^{\sin(x)} + C \).
- 📉 The process of checking the correctness of an integral by differentiating the result is emphasized, ensuring the solution is verified.
- 🧩 The lecture discusses a more complex example involving the integral of \( x \sqrt{x-1} \, dx \), illustrating the process of finding a suitable substitution.
- 📌 The importance of choosing a substitution that simplifies the integrand is stressed, as seen in the example with \( \csc(\theta) \cot(\theta) \, d\theta \).
- 🧬 The Gompertz model for tumor growth is introduced, and its differential equation is solved using separation of variables and u-substitution.
- 📈 The behavior of the tumor growth model is analyzed, revealing equilibria and the concept of carrying capacity in the context of the model.
- 🔠 The change of variables formula is presented as a broader concept that will be further explored in multivariable calculus, emphasizing its utility in simplifying complex integrals.
- 🔑 The lecture concludes by positioning u-substitution as the first in a sequence of integration techniques, with integration by parts being introduced in the next lesson.
Q & A
What is the main topic of Professor Greist's lecture 21?
-The main topic of lecture 21 is the method of substitution in calculus, specifically how to compute antiderivatives using substitution.
How does the linearity rule for derivatives relate to integration?
-The linearity rule for derivatives states that the derivative of a sum is the sum of the derivatives. This rule, when integrated, implies that integration is also linear, meaning the integral of a sum is the sum of the integrals, and the integral of a constant times an integrand is the constant times the integral of the integrand.
What is the u-substitution formula in integration?
-The u-substitution formula is given by ∫f(u)du = ∫f(u)du/dx dx, which is essentially the chain rule in reverse. It allows for the simplification of complex integrals by substituting u for a function of x and du for dx.
Can you provide an example of using u-substitution to solve an integral?
-An example given in the script is the integral of e^(sin(x))cos(x) dx. By letting u = sin(x), du = cos(x) dx, the integral becomes ∫e^u du, which is e^u + C, and after substituting back, it evaluates to e^(sin(x)) + C.
How can you verify the correctness of an integral solution?
-You can verify the correctness of an integral solution by differentiating the solution and checking if it matches the original integrand.
What is the Gompertz model for tumor growth?
-The Gompertz model is a differential equation that describes the size of a tumor as a function of time, given by dN/dt = -a * N * log(B * N), where a and B are constants, and N is the tumor size.
How does the Gompertz model show the behavior of a tumor's growth?
-The Gompertz model, when solved, shows that the tumor size N(t) follows a double exponential function, indicating that the growth rate slows down over time and eventually reaches an equilibrium at N = 1/B.
What are the equilibrium points in the Gompertz model?
-The equilibrium points in the Gompertz model are N = 0, which is an unstable equilibrium, and N = 1/B, which is a stable equilibrium known as the carrying capacity of the model.
Why is the method of substitution also known as the change of variables formula?
-The method of substitution is also known as the change of variables formula because it involves changing from x variables to u variables, which simplifies the integral and makes it easier to compute.
What is the significance of the change of variables technique in multivariable calculus?
-In multivariable calculus, the change of variables technique is used to solve more complex integrals by transforming them into simpler forms, which prepares students for more sophisticated problems.
What is the next integration technique that will be introduced after substitution?
-The next integration technique to be introduced after substitution is integration by parts.
Outlines
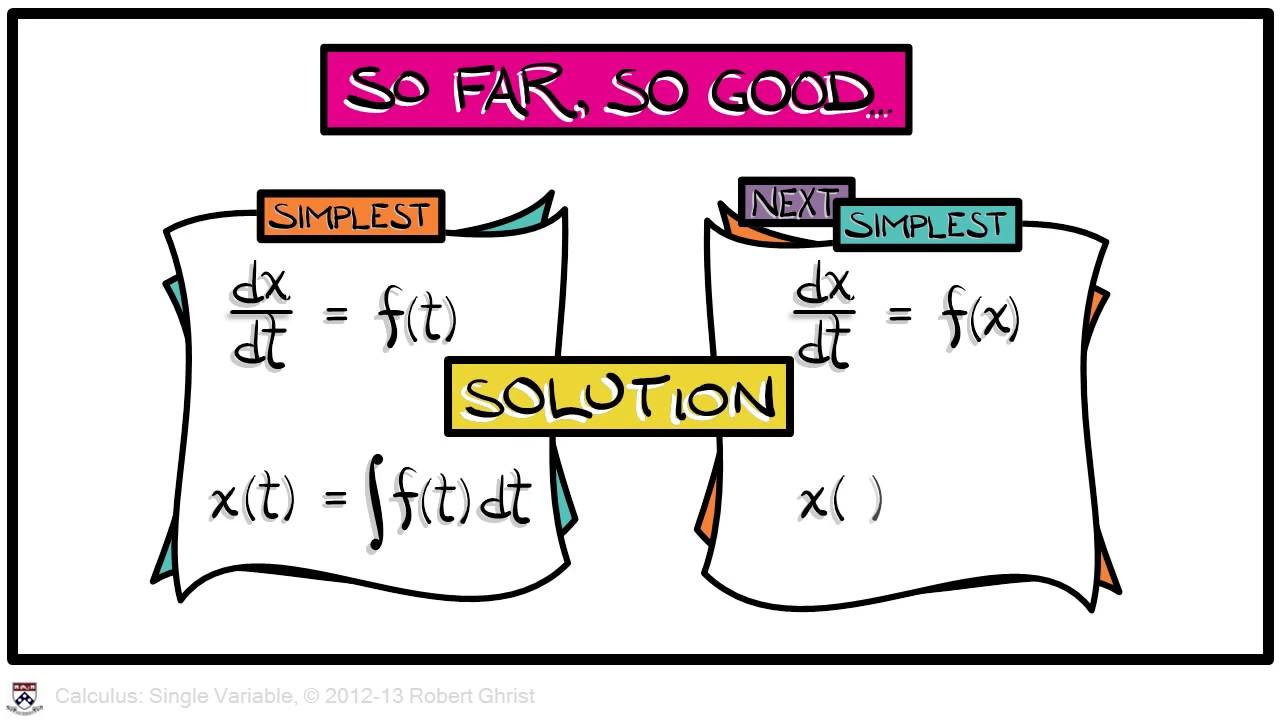
📚 Introduction to Substitution in Calculus
Professor Greist introduces the concept of substitution as a method for computing integrals in calculus. The lecture begins by explaining the linearity of integration, which is derived from the linearity of differentiation. The professor then demonstrates the u-substitution technique, using the chain rule in reverse, to simplify complex integrals. An example is given where the integral of e^(sin(x))cos(x) dx is simplified by setting u = sin(x), leading to an easier integral to solve. The process of checking the solution by differentiation is also discussed, emphasizing the importance of verification in mathematical problems. The paragraph concludes with a more challenging example involving the integral of x*sqrt(x-1) dx, illustrating the thought process behind choosing the appropriate substitution.
🔍 Advanced Substitution Examples and Tumor Growth Model
This paragraph delves into more complex examples of u-substitution, including the integral of cosec(θ)cot(θ) dθ, which simplifies to an integral in terms of u after substituting u = sin(θ). The professor shows how the integral can be solved by recognizing patterns that match known integral forms. The paragraph then transitions to a real-world application, the Gompertz model for tumor growth, which is a differential equation. The method of separation is used to rearrange the equation, and u-substitution is applied to solve the resulting integral. The solution is then expressed in terms of the original variable, n, the tumor size, and the behavior of the solution is analyzed in terms of equilibria, showing that the tumor size approaches a carrying capacity over time.
🌐 The Concept of Equilibria and the Importance of Change of Variables
The final paragraph discusses the concept of equilibria in the context of the tumor growth model, identifying stable and unstable equilibrium points by setting the rate of change of the tumor size to zero. The behavior of different solutions is analyzed, showing that they converge to the stable equilibrium. The paragraph then connects the u-substitution method to the broader concept of change of variables, which is crucial for solving more complex integrals in multivariable calculus. The professor emphasizes the importance of mastering simple substitution techniques as a foundation for tackling more intricate integration methods in future studies.
Mindmap
Keywords
💡Substitution
💡Integration
💡Linearity Rule
💡Chain Rule
💡Antiderivatives
💡Differential Equations
💡U-Substitution
💡Exponential Function
💡Trigonometric Functions
💡Carrying Capacity
💡Equilibria
💡Multivariable Calculus
Highlights
Introduction to Lecture 21 on substitution in calculus by Professor Greist.
Substitution as the first method for computing integrals, derived from differentiation rules.
Explanation of the linearity of integration, similar to differentiation.
Use of the chain rule in reverse for u-substitution in integrals.
Example of integrating e^(sin(x)) * cos(x) using u-substitution.
Verification of the integral result by differentiation.
Application of u-substitution in a more complex integral involving x * sqrt(x - 1).
Simplification of the integrand by choosing an appropriate substitution.
Integration of 1/u^2 using u-substitution with u = sin(theta).
Derivation of the Gumpert model for tumor growth using differential equations.
Method of separation applied to the Gumpert model to simplify the equation.
Integration of the separated equation using a suitable substitution.
Exponentiation to solve for the tumor size as a function of time.
Analysis of the equilibrium points in the Gumpert model.
Graphical representation of the tumor growth model and its equilibria.
Introduction to the concept of carrying capacity in the context of the tumor growth model.
Differentiation between stable and unstable equilibria in the model.
Importance of the change of variables formula in multivariable calculus.
Connection between substitution and the chain rule for complex functions.
Preview of the next lesson on integration by parts.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: