Calculus Chapter 3 Lecture 17 Indefinite Integrals
TLDRIn this calculus lecture, Professor Greist introduces indefinite integrals as antiderivatives, explaining their relationship with differentiation and their applications in solving differential equations. He demonstrates how integrals can represent the slope of a solution curve and shows how to solve basic differential equations using integration, including those involving gravity and exponential functions. The lecture also touches on the method of series and separation of variables to find solutions to linear differential equations, emphasizing the importance of the constant of integration and the prevalence of the exponential function e in various contexts.
Takeaways
- 📚 The lecture introduces the concept of the indefinite integral and its applications in differential equations.
- 🔄 The indefinite integral of a function is the anti-derivative of that function, reversing the process of differentiation.
- ⚠️ Integrating a function and then differentiating it returns the original function, except for an added constant of integration.
- 📈 Indefinite integrals produce a family of functions differing by a constant.
- ✔️ Basic integrals include power functions, trigonometric functions, and exponential functions, with constants of integration.
- 🧩 Some functions have complex antiderivatives, like \( e^{x^2} \), requiring advanced methods to solve.
- 💡 Indefinite integrals are crucial for solving differential equations, which describe relationships involving derivatives.
- 🌐 The simplest differential equation, \( \frac{dX}{dT} = f(T) \), has solutions that are indefinite integrals of \( f(T) \).
- 🪂 A practical example is modeling free-fall motion with differential equations involving gravity, velocity, and height.
- 🔢 Solving differential equations often involves series expansions or separation of variables, showing the integral's importance.
Q & A
What is the primary focus of Chapter 3 in Professor Greist's calculus lecture?
-Chapter 3 focuses on integration, specifically the indefinite integral, its applications, and motivations in differential equations.
How is the indefinite integral of a function f(x) defined?
-The indefinite integral of a function f(x) is defined as the antiderivative of f. If you differentiate the integral of f, you get back f.
Why is the indefinite integral considered almost but not exactly the inverse of differentiation?
-The indefinite integral is almost the inverse of differentiation because when you integrate a derivative, you get back the original function plus a constant of integration.
What is the integral of x^k and under what condition does this formula not apply?
-The integral of x^k is x^(k+1)/(k+1), except when k equals -1, in which case the integral is the natural logarithm of x, ln(x).
Why are some antiderivatives considered highly non-trivial to compute?
-Some antiderivatives are considered highly non-trivial to compute because they involve complex functions for which no straightforward antiderivative exists, such as e^(x^2).
What role does the constant of integration play in the solution to a differential equation?
-The constant of integration represents an initial condition in the solution to a differential equation. It shows that the solutions form a family of functions differing by a constant.
How is the simplest differential equation of the form dx/dt = f(t) solved?
-The simplest differential equation dx/dt = f(t) is solved by integrating f(t) with respect to t, resulting in the function x(t) plus a constant of integration.
How is the motion of a falling object modeled using differential equations?
-The motion of a falling object is modeled using the differential equation dv/dt = -g for velocity and dx/dt = v for position, where g is the constant acceleration due to gravity.
What is the general solution to the differential equation dv/dt = -g?
-The general solution to dv/dt = -g is v(t) = -gt + C, where C represents the initial velocity of the object.
How do you solve the differential equation dx/dt = ax for x(t)?
-The differential equation dx/dt = ax is solved by finding x(t) = Ce^(at), where C is a constant determined by initial conditions.
What is the method of separation of variables and how is it used to solve dx/dt = ax?
-The method of separation of variables involves moving all x terms to one side of the equation and all t terms to the other side, then integrating both sides. For dx/dt = ax, this results in ln(x) = at + C, leading to x(t) = Ce^(at).
Why does the constant 'e' frequently appear in solutions to differential equations?
-The constant 'e' frequently appears in solutions to differential equations because the exponential function e^(at) is a natural solution to equations of the form dx/dt = ax, where the function's derivative is proportional to itself.
What is the significance of the constant of integration in the context of differential equations?
-The constant of integration in differential equations represents an initial condition or an arbitrary constant that accounts for the family of possible solutions differing by a constant value.
Outlines
📚 Introduction to Indefinite Integrals and Their Role in Differential Equations
Professor Greist introduces the concept of indefinite integrals, explaining them as antiderivatives of functions. He clarifies that while integrals are almost inverses to differentiation, they involve a constant of integration. The professor provides examples of simple integrals, such as those of polynomials, sines, cosines, and exponential functions, emphasizing the inclusion of constants. He then connects the concept to differential equations, highlighting how the indefinite integral is used to solve basic differential equations, such as those describing the motion of objects under gravity, and introduces the concept of ordinary differential equations (ODEs).
🌐 Gravitational Motion and Solving Differential Equations with Initial Conditions
The script delves into the application of differential equations to model the motion of a falling object under the influence of gravity. It outlines how to set up and solve differential equations for velocity and height as functions of time, incorporating initial conditions to represent initial velocity and height. The professor explains how the solutions to these equations, which include constants of integration, can be interpreted as initial conditions, leading to the familiar parabolic motion equation from basic physics.
🔍 Exploring Methods to Solve Differential Equations: Anzats and Series Expansions
The video script discusses different methods for solving differential equations, starting with the Anzats method, where a guess is made and verified as a solution. The professor then introduces a more systematic approach using series expansions, where the function is assumed to have a series form and coefficients are determined by equating terms on both sides of the differential equation. This method leads to a solution involving exponential functions, which is consistent with the Anzats method but derived through a more rigorous process.
📈 The Power of Integration in Solving Differential Equations: Separation of Variables
The final paragraph focuses on the method of separation of variables as a powerful technique for solving differential equations. The professor demonstrates how to rearrange terms and apply integration to both sides of the equation to find the solution. The solution is presented in the form of an exponential function multiplied by an arbitrary constant, which can be interpreted as an initial condition. The script emphasizes the recurring role of the exponential function in solving differential equations and the importance of understanding the constant of integration in various contexts.
Mindmap
Keywords
💡Indefinite Integral
💡Anti-derivative
💡Constant of Integration
💡Differential Equations
💡Derivative
💡Integration by Parts
💡Logarithmic Functions
💡Exponential Functions
💡Trigonometric Functions
💡Initial Conditions
💡Separation of Variables
Highlights
Introduction to indefinite integrals as antiderivatives and their relationship with differentiation.
The concept of the constant of integration and its implications for the indefinite integral.
Simple integrals of polynomials, exponentials, and trigonometric functions.
The challenge of finding antiderivatives for complex functions like e^(x^2).
The relevance of indefinite integrals in solving differential equations.
The interpretation of derivatives as slopes and their connection to differential equations.
Solutions to differential equations as families of curves depending on constants.
Application of integration to model the motion of objects under gravity.
Derivation of the basic physics formula for projectile motion using integration.
The distinction between ordinary and extraordinary differential equations.
Solving the canonical differential equation DX/DT = aX using separation of variables.
The method of solution by ansatz and its application to differential equations.
The series approach to solving differential equations and its connection to the exponential function.
The pattern in the coefficients of the series expansion for solving differential equations.
The principled approach to solving differential equations using series and induction.
The method of separation as a powerful technique for solving differential equations.
The ubiquity of the exponential function e^(aT) in solutions to differential equations.
The integration of e as a recurring theme in calculus, series, and differential equations.
The upcoming focus on solutions to differential equations and the role of integration in understanding them.
Transcripts
Browse More Related Video

Business Calculus - Math 1329 - Section 5.1 - Indefinite Integration & Differential Equations
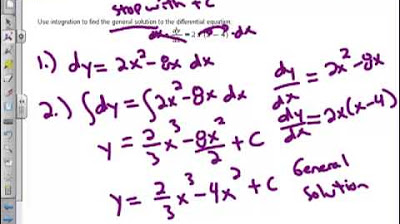
Differential Equations BC Calculus

Integrating Exponential Functions
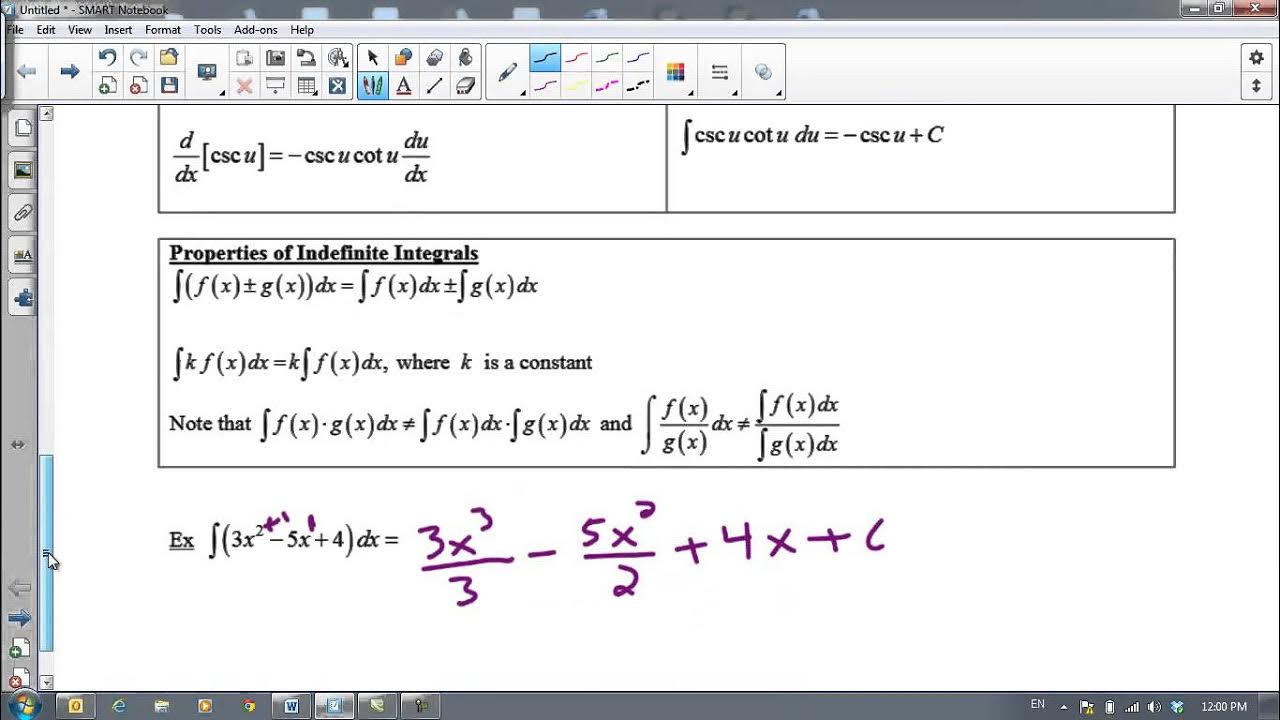
Antiderivatives and Indefinite Integrals

AP Calculus Differential Equations Review (All of Unit 7)

Special Integration in a Linear Differential Equation Problem (Differential Equations 18)
5.0 / 5 (0 votes)
Thanks for rating: