Average Value of a Continuous Function

Chad Gilliland
11 Nov 201312:19
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video discusses the Mean Value Theorem for integrals, explaining how the average value of a continuous function on a closed interval can be represented as a rectangle with the same area under the curve. It demonstrates how to calculate average values geometrically and through Riemann sums, using examples like average speed and stock prices.

Takeaways
  • 📚 The Mean Value Theorem for integrals states that if a function 'f' is continuous on a closed interval [A, B], there exists a 'C' within that interval such that the integral from A to B of 'f(x)' dx equals 'f(C)' times (B - A).
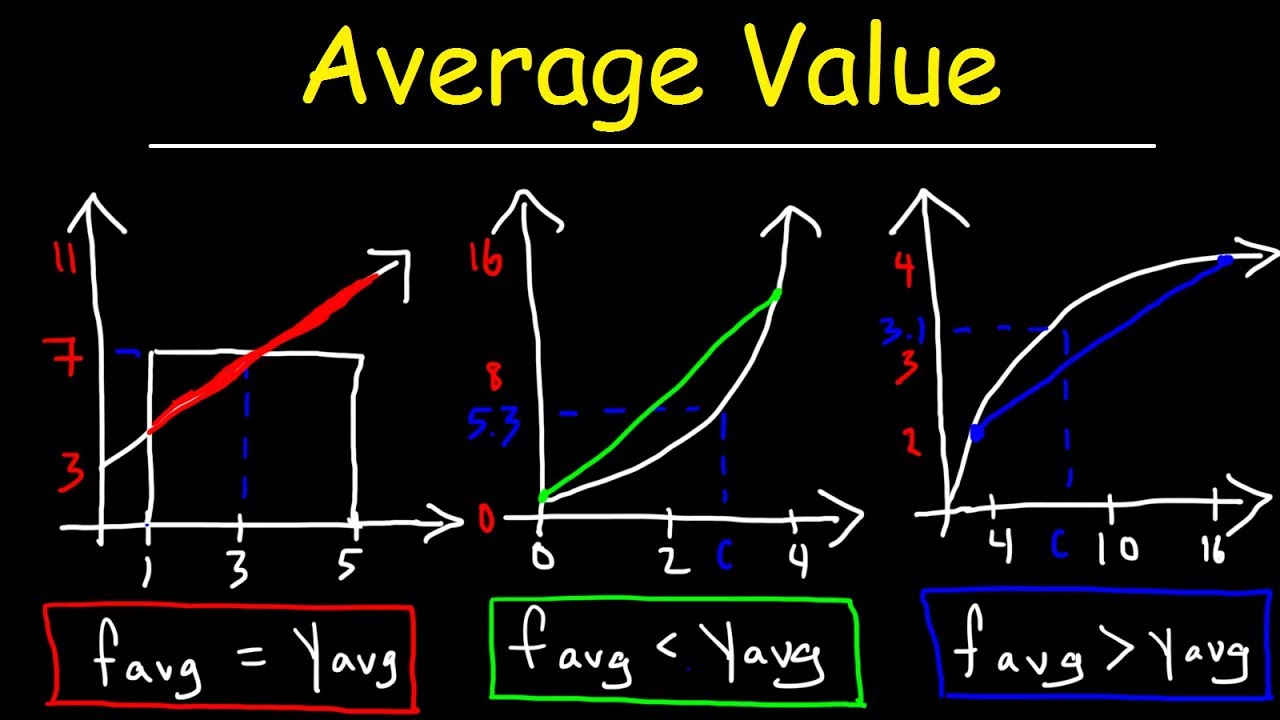
  • 📈 The geometric interpretation of the Mean Value Theorem for integrals suggests that any continuous curve can be represented by a rectangle with the same area, where the height of the rectangle is 'f(C)' at some point 'C' within the interval.
  • 📊 The concept of 'average value' of a continuous function can be visualized as the 'average height' of the graph, which is the height of the rectangle that matches the area under the curve.
  • 🔍 To find the average value of a function, one can divide the area under the curve by the width of the interval, which is (B - A).
  • 📘 An antiderivative of a function can be used to evaluate the integral from a specific interval and subsequently find the average value of the function over that interval.
  • 👉 The Mean Value Theorem for integrals can be applied to practical scenarios, such as calculating average speed from a speed graph or the average value of a stock from its price graph.
  • 📝 When a function is not defined by an explicit equation, Riemann sums can be used to approximate the integral and estimate the average value.
  • 📉 In the context of traffic speed, the average speed over a certain time period can be calculated using the Mean Value Theorem for integrals by integrating the speed function over that period.
  • 📐 For piecewise functions, the average value can be found by calculating the combined areas of the geometric shapes formed by the function and then dividing by the width of the interval.
  • 📝 The script provides an example of calculating the average value of a function defined by a quadratic equation over a given interval without integration, by finding the 'C' value where the average height equals 'f(C)'.
  • 📚 The script concludes with an example of estimating the average value of a function using a left Riemann sum and emphasizes the importance of understanding the geometric interpretation of the Mean Value Theorem for integrals.
Q & A

  • What is the Mean Value Theorem for integrals?

    -The Mean Value Theorem for integrals states that if a function f is continuous on the closed interval [a, b], then there exists a number c in the closed interval [a, b] such that the integral from a to b of f(x) dx equals f(c) times (b - a). This theorem implies that the area under the curve of a continuous function can be represented as a rectangle with the same area, where the height of the rectangle is f(c) and the width is (b - a).

  • What does the average value of a continuous function represent geometrically?

    -Geometrically, the average value of a continuous function represents the height of a rectangle that has the same area as the area under the curve of the function from a to b. This rectangle is constructed by finding a value c within the interval [a, b] where the function intersects a line parallel to the x-axis at height f(c).

  • How can you find the average value of a function using the Mean Value Theorem for integrals?

    -To find the average value of a function using the Mean Value Theorem for integrals, you divide the integral of the function from a to b by the width of the interval (b - a). This gives you the average height, which is the average value of the function over the interval.

  • What is the formula for finding the average value of a function on a given interval?

    -The formula for finding the average value of a function f on the interval [a, b] is given by (1/(b - a)) times the integral from a to b of f(x) dx.

  • How is the average value of a function related to the concept of average speed?

    -The average value of a function can be related to the concept of average speed. For example, if you have a speed graph, the average speed over a certain time interval can be found by calculating the area under the curve (representing the total distance traveled) and dividing it by the width of the interval (representing the time).

  • What is the significance of the value c in the context of the Mean Value Theorem for integrals?

    -The value c in the context of the Mean Value Theorem for integrals is significant because it is the point at which the function intersects a horizontal line that represents the average height of the function over the interval [a, b]. This line can be used to form a rectangle with the same area as the area under the curve.

  • How can you estimate the average value of a function using Riemann sums?

    -To estimate the average value of a function using Riemann sums, you divide the interval into subintervals and calculate the sum of the products of the function values at the left endpoints of each subinterval and the widths of the subintervals. This sum is then divided by the total width of the interval to estimate the average value.

  • What is the formula for finding the average speed of traffic between two hours using the Mean Value Theorem for integrals?

    -The formula for finding the average speed of traffic between two hours (1 and 4, for example) is given by (1/(4 - 1)) times the integral from 1 to 4 of the speed function s(t) dt.

  • How can you use the Mean Value Theorem for integrals to find the average value of a piecewise function?

    -To find the average value of a piecewise function using the Mean Value Theorem for integrals, you can calculate the integral of each piece of the function over its respective interval and then sum these integrals. The total area under all the pieces is then divided by the total width of the interval to find the average value.

  • What is the geometric interpretation of the average value of a function in terms of triangles?

    -In the geometric interpretation, the average value of a function can be represented by the combined areas of triangles formed under the curve of the function. The average value is then the sum of these areas divided by the width of the interval, which gives the average height of these triangles.

Outlines
00:00
📚 Introduction to the Mean Value Theorem for Integrals

This paragraph introduces the Mean Value Theorem for integrals, which states that for a continuous function on a closed interval, there exists a point within that interval where the function's value is equal to the average value of the function over that interval. The explanation uses the analogy of a rectangle with the same area as the area under the curve of the function. The speaker illustrates this concept with a graph, explaining how to find the 'perfect rectangle' that represents the average height of the function and provides an example using the function 1 + x^2 to find its average value over a given interval.

05:03
📈 Applying the Mean Value Theorem to Practical Examples

The speaker demonstrates the application of the Mean Value Theorem in real-world scenarios, such as calculating average speed from a speed graph or the average value of a stock from its price graph. The formula for the average value of a function is presented, and the speaker explains how to use it to find the average height or value of a function by dividing the area under the curve by the width of the interval. An example with a function 1 + x^2 is worked through, showing the process of finding the antiderivative and evaluating it at the interval's endpoints to find the average value.

10:05
📊 Estimating Average Values with Riemann Sums

This paragraph discusses the use of Riemann sums to estimate the average value of a function when an explicit function is not available. The speaker provides an example of estimating the average value of a function over an interval using a left Riemann sum with three subintervals. The process involves calculating the sum of the product of the width of each subinterval and the function's value at the left endpoint, and then dividing by the total width of the interval. The speaker also touches on the geometric interpretation of the average value and provides an example of a piecewise function to illustrate finding the average value without integration by calculating the areas of geometric shapes under the curve.

Mindmap
Keywords
💡Average Value
The average value of a continuous function is calculated by dividing the area under the curve by the width of the interval. It represents the average height of the function over a specified range. For example, in the script, the average value is calculated for the function 1 + x² over the interval [-1, 2].
💡Mean Value Theorem for Integrals
The Mean Value Theorem for Integrals states that if a function f is continuous on the closed interval [a, b], then there exists a number c in [a, b] such that the integral of f from a to b equals f(c) times (b - a). This theorem is used to demonstrate that the area under a curve can be represented by a rectangle with height f(c) and width (b - a).
💡Integral
An integral represents the area under a curve of a function. In the script, integrals are used to calculate the area under the function f(x) from a to b, which is then used to determine the average value of the function. For example, the integral of 1 + x² from -1 to 2 is computed to find the average value of the function over that interval.
💡Rectangle Approximation
Rectangle approximation is a method used to estimate the area under a curve by dividing it into rectangles. The script explains how any continuous curve can be approximated by a rectangle with the same area, height f(c), and width (b - a). This is a key concept in understanding the application of the Mean Value Theorem for Integrals.
💡Antiderivative
An antiderivative is a function whose derivative is the original function. In the script, the antiderivative of the function 1 + x², which is x + x³/3, is used to evaluate the integral from -1 to 2. Finding the antiderivative is a crucial step in computing definite integrals.
💡Riemann Sum
A Riemann Sum is a method for approximating the total area under a curve by summing the areas of multiple rectangles. The script discusses using a left Riemann sum to estimate the integral of a function when the explicit equation is not given. For example, the left Riemann sum is used to approximate the integral of a function over the interval [5, 17].
💡Subintervals
Subintervals are divisions of the interval over which the integral is computed. In the script, subintervals are used to calculate Riemann sums, with each subinterval contributing to the total approximation of the area under the curve. The left Riemann sum method mentioned in the script divides the interval [5, 17] into subintervals to estimate the average value.
💡Piecewise Function
A piecewise function is defined by different expressions in different intervals. In the script, a piecewise function consisting of two linear segments, 3 - x from -1 to 3 and 2x - 6 from 3 to 6, is used to demonstrate calculating the average value without direct integration. The total area under the curve is found by summing the areas of the two triangles formed by the piecewise segments.
💡Signed Area
Signed area refers to the area under a curve, considering the direction above or below the x-axis. Positive areas are above the x-axis, and negative areas are below. The script mentions the signed area in the context of calculating the integral of the piecewise function, where the net signed area determines the total integral value.
💡Average Speed
Average speed is the total distance traveled divided by the total time taken. In the script, the average speed of traffic between 1 PM and 4 PM is calculated using an integral of the speed function over this interval. The integral represents the total distance, and dividing by the time interval gives the average speed.
Highlights

Introduction to the average value of a continuous function.

The Mean Value Theorem for integrals states that for a continuous function on a closed interval, there exists a number within that interval where the integral equals the function value times the interval width.

Geometric interpretation of the Mean Value Theorem: any continuous curve can be represented as a rectangle with the same area as the area under the curve.

Demonstration of the Mean Value Theorem through a graphical representation.

Explanation of how to find the average height or value of a function by dividing the area under the curve by the interval width.

Application of the Mean Value Theorem in calculating average speed from a speed graph.

Example calculation of the average value of a function using integration.

Finding the value of C that makes the average value of the function equal to F(C).

Graphical estimation of the average value of a function without integration.

Using Riemann sums to estimate the average value of a function.

Calculating average speed using a traffic speed formula and integration.

Explanation of how to compute the average speed of traffic between specific hours using integration.

Demonstration of using Riemann sums geometrically to find the exact answer without integration.

Calculating the average value of a piecewise function by estimating the areas of triangles formed under the curve.

Final summary of the lesson on calculating average value and its applications.

Transcripts

Browse More Related Video

Average Value of a Function Over an Interval - Calculus

The Mean Value Theorem For Integrals: Average Value of a Function

Average Value of a Continuous Function on an Interval

Mean value theorem for integrals | AP Calculus AB | Khan Academy

Calculus: Average Value of a Function (Section 6.5) | Math with Professor V

AP Calculus AB: Lesson 6.5 Accumulation of Change

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Mean Value TheoremIntegral CalculusAverage ValueContinuous FunctionsGeometric InterpretationRiemann SumsSpeed GraphStock PricesTraffic SpeedPiecewise FunctionsCalculus Applications