Average Value of a Function Over an Interval - Calculus

The Organic Chemistry Tutor
10 Mar 201818:57
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the concept of finding the average value of a function over a given interval. It explains the process using three different functions: linear, quadratic, and square root. The script highlights that for a linear function, the average value equals the average y-value, but this relationship varies for non-linear functions. It also introduces the mean value theorem and demonstrates how to calculate the average value and the corresponding x-value (c) where the area under the curve equals the area of the rectangle, using definite integrals and anti-derivatives.

Takeaways
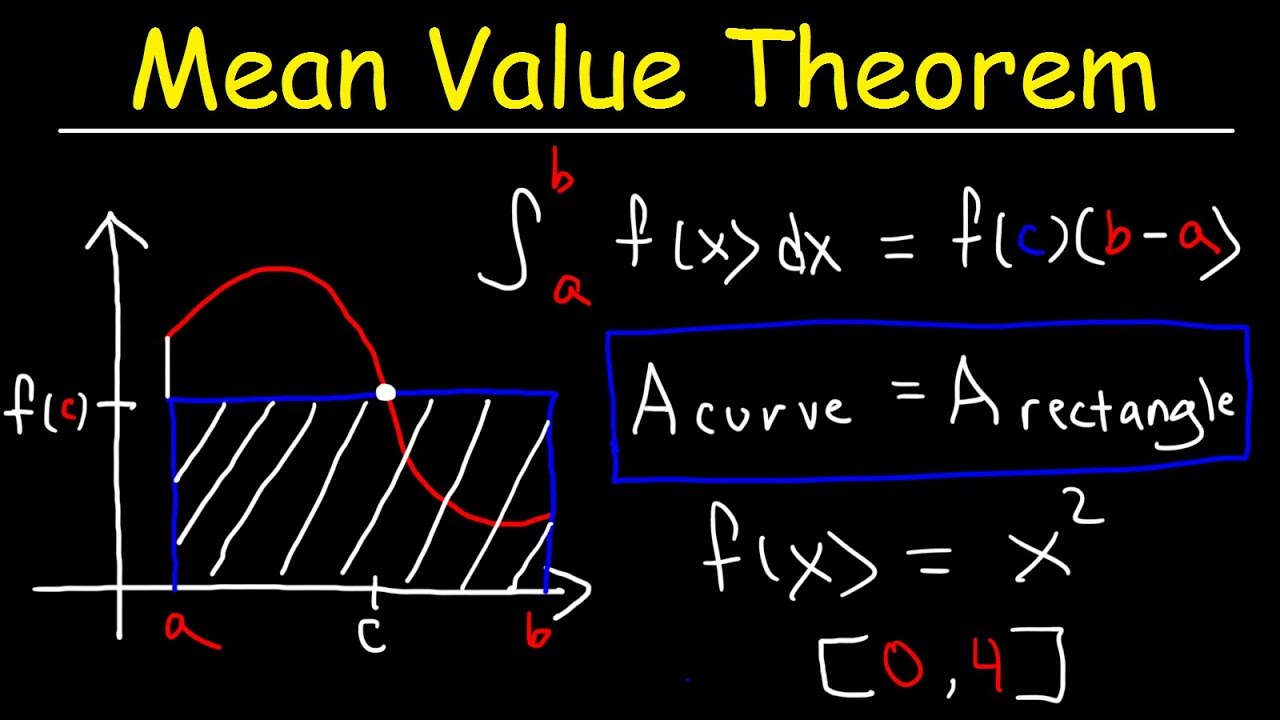
  • 📈 The average value of a function over an interval can be found using the definite integral and the Mean Value Theorem.
  • 🌟 For a linear function, the average value of the function equals the average y-value on the interval.
  • 🔍 The value 'c' in the average value formula (1/(b-a) * ∫[a to b] f(x) dx) represents the x-value where the area under the curve equals the area of the rectangle.
  • 📌 In the case of the function f(x) = 2x + 1 from x=1 to x=5, the average value is 7, which is the same as the average y-value.
  • 🚫 For non-linear functions, the average value of the function may not equal the average y-value.
  • 📶 The average value of the function can be greater, less than, or equal to the average y-value depending on the shape of the curve.
  • 🌡️ For the function f(x) = x^2 from x=0 to x=4, the average value is approximately 5.33, which is less than the average y-value of 8.
  • 🌱 For the function f(x) = √x from x=4 to x=16, the average value is 28/9, which is greater than the average y-value of 3.
  • 📍 The value of 'c' does not always correspond to the midpoint of the interval 'a' and 'b', especially for non-linear functions.
  • 🔧 The process of finding 'c' involves taking the square root of the average value and solving for 'x' when f(x) is not a linear function.
  • 🔍 Analyzing the secant line in relation to the curve of the function can help understand why the average function value may vary from the average y-value.
Q & A

  • What is the given linear function in the script?

    -The given linear function is f(x) = 2x + 1.

  • What is the interval considered for finding the average value of the function?

    -The interval considered is from 1 to 5.

  • How is the average value of a function over an interval defined?

    -The average value of a function over an interval is defined as (1 / (b - a)) * ∫[a to b] f(x) dx, where 'a' and 'b' are the endpoints of the interval.

  • What is the y-intercept of the given linear function?

    -The y-intercept of the given linear function is 1.

  • What is the slope of the linear function?

    -The slope of the linear function is 2.

  • What is the average y value for the linear function over the interval [1, 5]?

    -The average y value for the linear function over the interval [1, 5] is 7.

  • How does the average value of a linear function compare to the average y value?

    -For a linear function, the average value of the function is equal to the average y value over the interval from 'a' to 'b'.

  • What is the average x value for the interval [1, 5]?

    -The average x value for the interval [1, 5] is 3, which is the midpoint of the interval.

  • What is the value of 'c' for the linear function that makes the area under the curve equal to the area of the rectangle?

    -For the linear function, 'c' is equal to the average x value, which is 3.

  • How does the average value of a function change if the function is not linear?

    -If the function is not linear, the average value of the function may not be equal to the average y value. It depends on the shape of the curve relative to the secant line between the interval endpoints.

  • What is the significance of the value 'c' in the context of the mean value theorem?

    -In the context of the mean value theorem, 'c' is the value at which the function's value equals the average value over the interval, making the area under the curve equal to the area of the rectangle formed by the secant line and the x-axis.

Outlines
00:00
📊 Calculating the Average Value of a Linear Function

This paragraph discusses the method of finding the average value of a linear function, f(x) = 2x + 1, over the interval from 1 to 5 using a straw graph and the mean value theorem. It explains that the average value corresponds to the y-coordinate of the point where the area under the curve equals the area of the rectangle with height f(c) and width (b-a). The calculation involves evaluating the definite integral from a to b and dividing by (b-a), resulting in an average value of 7, which is the same as the average y-value in the interval for a linear function.

05:00
📈 Comparing Average Values for Non-Linear Functions

The second paragraph explores the concept of average value for non-linear functions, using the example of f(x) = x^2 over the interval from 0 to 4. It contrasts the average y-value (8) with the average function value (approximately 5.33), highlighting that for non-linear functions, the average function value may not equal the average y-value. The paragraph also introduces the concept of the average x-value and demonstrates how to calculate the value of c that corresponds to the average function value, which is found to be approximately 2.309, greater than the average x-value of 2.

10:01
🌟 Analyzing Function Behavior with Average Values

This paragraph delves into the behavior of functions by comparing their average values with the average y-values over specified intervals. It presents a third example with f(x) as the square root of x over the interval from 4 to 16 and shows that the average function value (approximately 3.1) can be greater than the average y-value (3). The paragraph emphasizes that for linear functions, the average function value equals the average y-value, but this relationship varies for non-linear functions. It visually represents the three functions graphed and explains how the position of the curve relative to the secant line affects the relationship between the average function value and the average y-value.

Mindmap
Keywords
💡Linear Function
A linear function is a mathematical function that has the form f(x) = mx + b, where m is the slope and b is the y-intercept. In the video, the linear function f(x) = 2x + 1 is used to demonstrate the concept of average value over an interval. The graph of this function is a straight line with a slope of 2 and a y-intercept of 1, which is used to explain the mean value theorem and the calculation of the average value of the function over the interval from 1 to 5.
💡Mean Value Theorem
The Mean Value Theorem is a fundamental theorem in calculus that states that for a continuous function on a closed interval [a, b], there exists at least one number c in the open interval (a, b) such that the average value of the function over the interval is equal to the function's value at c. In the video, this theorem is used to explain why the average value of a linear function over an interval is the same as the average of the function's values at the endpoints of the interval.
💡Definite Integral
A definite integral is a mathematical concept used to calculate the area under the curve of a function over a specified interval. It is denoted as ∫[a, b] f(x) dx. In the context of the video, the definite integral is used to find the area under the curve of the function f(x) = 2x + 1 from x = 1 to x = 5, which helps in determining the average value of the function over that interval.
💡Average Value
The average value of a function over an interval is the mean of the values that the function takes on over that interval. It is calculated by dividing the integral of the function over the interval by the length of the interval. In the video, the concept of average value is central to understanding how the mean value theorem applies to linear and non-linear functions.
💡Y-Intercept
The y-intercept is the point at which a linear function crosses the y-axis on a graph. It is the value of y when x is equal to zero. In the video, the y-intercept of the linear function f(x) = 2x + 1 is 1, which means the graph of the function crosses the y-axis at the point (0, 1).
💡Slope
The slope of a linear function is a measure of how steep the line is, or in other words, the rate of change of the function with respect to x. It is the coefficient of x in the function's equation. In the video, the slope of the linear function f(x) = 2x + 1 is 2, indicating that for every unit increase in x, the function's value increases by 2 units.
💡Interval
In mathematics, an interval refers to a set of real numbers that fall within a certain range. It is used to define the domain over which a function is being considered or the range of values that a variable can take. In the video, the interval [1, 5] is the range over which the average value of the function f(x) = 2x + 1 is calculated.
💡Anti-Derivative
An anti-derivative, also known as an integral, is a function that represents the area under the curve of another function, the derivative of which is the original function. In the context of the video, finding the anti-derivative of a function is essential for calculating definite integrals and, consequently, the average value of the function over a given interval.
💡Area Under the Curve
The area under the curve of a function refers to the region enclosed by the graph of the function and the x-axis over a specified interval. This area can be calculated using definite integrals and is a key concept in understanding the average value of a function over an interval. In the video, the area under the curve is used to illustrate the mean value theorem and the calculation of the average value.
💡Secant Line
A secant line is a straight line that intersects a curve at two or more points. In the context of the video, the secant line is used to compare the average function value with the average y-value of a non-linear function. The position of the secant line relative to the curve helps determine whether the average function value is greater than, less than, or equal to the average y-value.
💡Midpoint
The midpoint of an interval is the central point that divides the interval into two equal subintervals. It is calculated as the average of the endpoints of the interval. In the video, the midpoint is used to compare with the value of c, which is the x-value where the average function value occurs.
Highlights

Exploring the average value of a linear function f(x) = 2x + 1 over the interval [1, 5].

Using the Mean Value Theorem to find the average value of a function.

Calculating the area under the curve as the definite integral from a to b.

Deriving the formula for the average value as 1/(b-a) * integral from a to b of f(x) dx.

For a linear function, the average value is the average y-value in the interval a to b.

Finding c for the linear function, where the area under the curve equals the area of the rectangle.

The average value of the function is 7, which is the average y-value for the interval [1, 5].

Analyzing a non-linear function, f(x) = x^2, over the interval [0, 4].

Comparing the average value of the function to the average y-value and finding that they are different for non-linear functions.

Calculating the average value for f(x) = x^2 as 16/3, which is less than the average y-value of 8.

For the function f(x) = sqrt(x), finding the average value over the interval [4, 16] to be 28/9, greater than the average y-value of 3.

Observing that c for non-linear functions is not the midpoint of a and b, and the average function value is not the average y-value.

Drawing graphs for the three functions to visualize the relationship between average function value and average y-value.

Understanding that for a linear function, the average function value equals the average y-value, but this does not hold for non-linear functions.

Noting that the position of c relative to the average x-value depends on the nature of the function.

The average function value can be less than, equal to, or greater than the average y-value depending on the function's shape.

The significance of the function's shape in determining the relationship between the average function value and the average y-value.

Practical applications of understanding average values in various types of functions for problem-solving and analysis.

Transcripts

Browse More Related Video

The Mean Value Theorem For Integrals: Average Value of a Function

Mean Value Theorem For Integrals

Calculus: Average Value of a Function (Section 6.5) | Math with Professor V

Average Value of a Continuous Function

Average Value of a Continuous Function on an Interval

Mean value theorem for integrals | AP Calculus AB | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Calculus ConceptsAverage ValueLinear FunctionsNon-Linear FunctionsIntegral CalculusMathematical AnalysisMidpoint FormulaSecant LinesFunction ComparisonEducational Content