Calculus: Average Value of a Function (Section 6.5) | Math with Professor V
TLDRThis video script offers a comprehensive guide on calculating the average value of a function, with a detailed walkthrough of the process using integrals. It starts by explaining the concept of average value for both discrete numbers and functions, then demonstrates how to find the average value of specific functions, such as sine and secant squared, using integral formulas. The script also introduces the Mean Value Theorem for integrals, illustrating how to find a point 'C' where the function's value equals the average value over an interval. Examples are provided to solidify the concepts, with a focus on visual confirmation through graphing, ensuring a deeper understanding of the mathematical principles involved.
Takeaways
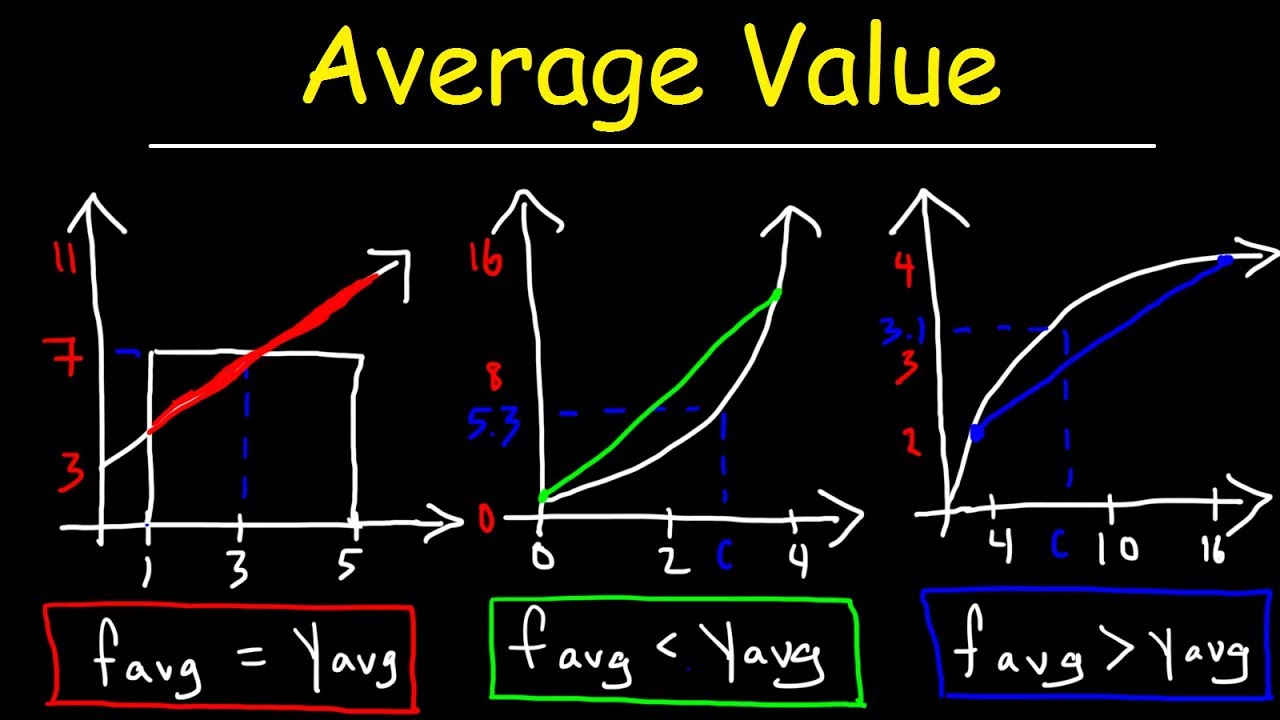
- 📚 The average value of a function over an interval can be found by integrating the function over the interval and dividing by the length of the interval.
- 🔍 To find the average value of f(x) = sine(4x) from -π to π, integrate sine(4x) and evaluate from -π to π, resulting in an average value of 0 due to the function's symmetry.
- 📈 The graph of y = sine(4x) confirms the average value calculation, showing symmetry about the origin and equal areas above and below the x-axis.
- 📘 The average value of a function can also be expressed as the integral of the function over an interval divided by the interval's length, similar to finding the mean of a set of numbers.
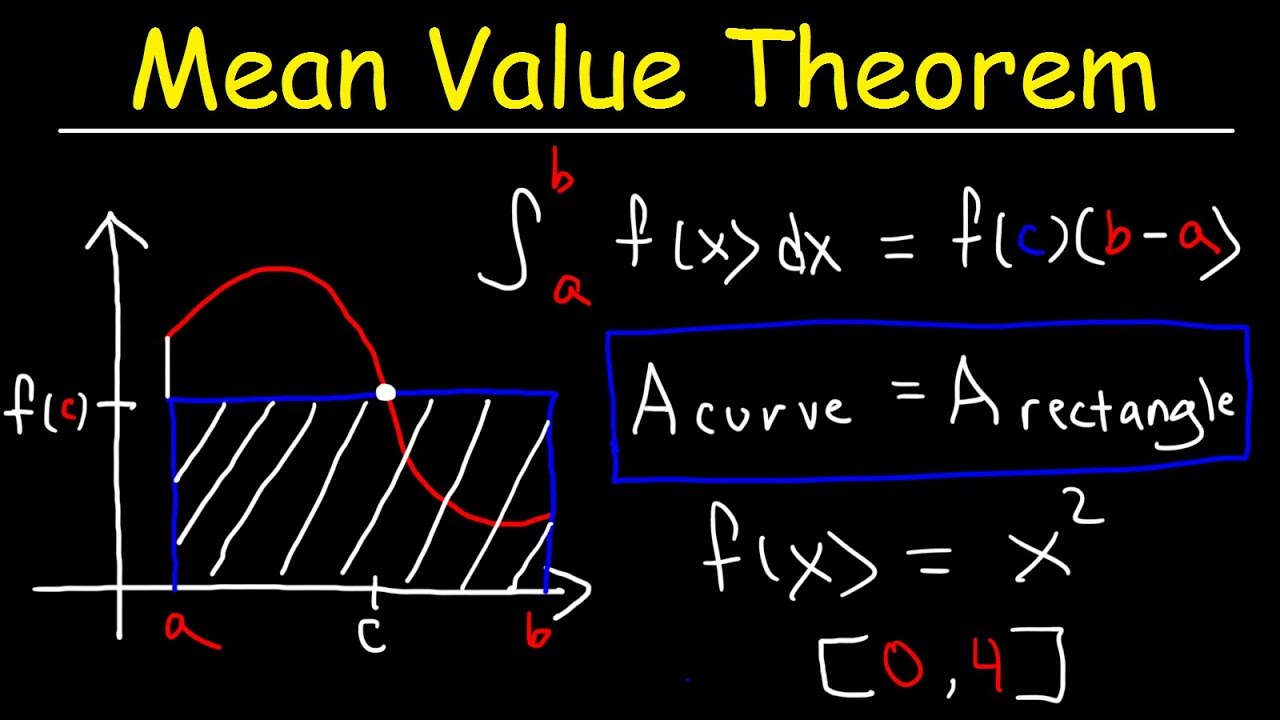
- 📌 The mean value theorem for integrals states that for a continuous function on a closed interval, there exists at least one point c in the interval where the function's value equals the average value of the function over that interval.
- 📐 For the function f(θ) = secant squared(θ/2) over the interval from 0 to π/2, the average value is calculated by integrating and evaluating the antiderivative from the interval limits.
- 📊 The mean value theorem for integrals can be visualized as finding a rectangle with the same area as the area under the curve of a continuous function over an interval.
- 📉 In the example with f(x) = sqrt(x) over [0, 4], the average value is computed and a specific value of c is found such that f(c) equals the average value.
- 📝 The process of finding the average value and applying the mean value theorem involves anti-differentiation and evaluation of integrals at the interval's endpoints.
- 📑 The script provides a step-by-step guide on how to calculate average values and apply the mean value theorem for integrals with practical examples.
Q & A
What is the definition of average value of a function on a given interval?
-The average value of a function on a given interval [A, B] is calculated by taking the integral of the function from A to B and dividing it by the length of the interval, which is (B - A).
How do you find the average value of the function f(x) = sin(4x) on the interval from -π to π?
-You integrate sin(4x) with respect to x from -π to π and then divide by the length of the interval, which is 2π. The antiderivative of sin(4x) is -cos(4x)/4. Evaluating this from -π to π results in an average value of 0 because cos(4π) - cos(-4π) = 1 - 1 = 0.
Why is the average value of the function f(x) = sin(4x) on the interval from -π to π equal to 0?
-The function sin(4x) is an odd function, and the interval from -π to π is symmetric about the origin. Due to this symmetry, the positive and negative values of the function over the interval cancel each other out, resulting in an average value of 0.
What is the antiderivative of secant squared of θ over 2?
-The antiderivative of secant squared θ over 2 is 2 times the tangent of θ over 2, which is obtained by applying the chain rule in reverse.
How do you find the average value of the function f(θ) = secant squared θ over 2 on the interval from 0 to π/2?
-You integrate secant squared θ over 2 with respect to θ from 0 to π/2 and then divide by the length of the interval, which is π/2. The antiderivative is 2 times the tangent of θ over 2, and evaluating this from 0 to π/2 gives an average value of 4/π.
What is the Mean Value Theorem for Integrals?
-The Mean Value Theorem for Integrals states that if a function is continuous on a closed interval [A, B], there exists at least one number C in that interval such that the function value at C times the length of the interval (B - A) is equal to the definite integral from A to B of the function.
How does the Mean Value Theorem for Integrals relate to the area under a curve?
-The Mean Value Theorem for Integrals implies that for a continuous function on an interval, there is a rectangle with the same area as the area under the curve of the function on that interval. The rectangle's height is the function's value at some point C in the interval, and its base is the length of the interval.
What is the average value of the function f(x) = √x on the interval from 0 to 4?
-The average value is found by integrating √x from 0 to 4 and dividing by the interval length, which is 4. The antiderivative of √x is (2/3)x^(3/2), and evaluating from 0 to 4 gives an average value of 4/3.
How do you find the value of C such that f(C) equals the average value of the function f(x) = √x on the interval from 0 to 4?
-You set √C equal to the average value, which is 4/3. Squaring both sides gives C = 16/9, which is the value within the interval that makes f(C) equal to the average value.
How can you visually confirm the Mean Value Theorem for Integrals using the function f(x) = √x on the interval from 0 to 4?
-By sketching the graph of f(x) = √x and drawing a rectangle with the height equal to the average value of the function (4/3) and the base equal to the length of the interval (4), you can see that the area of the rectangle matches the area under the curve, confirming the theorem.
Outlines
📚 Understanding Average Value of Functions
This paragraph introduces the concept of computing the average value of a function over an interval, akin to finding the mean of a set of numbers. The average value of a function f(x) on the interval [A, B] is given by the integral from A to B of f(x) divided by the interval length (B - A). The example provided calculates the average value of f(x) = sin(4x) over the interval [-π, π], using integration and anti-differentiation techniques. The result confirms that the average value is 0 due to the symmetry of the sine function, which is an odd function, and the interval's even split from -π to π.
📈 Calculating the Average Value of a Secant Squared Function
The second paragraph delves into another example of finding the average value, this time for the function f(θ) = secant squared θ/2 over the interval [0, π/2]. The process involves integrating the function and evaluating the result at the interval's endpoints. The anti-derivative of secant squared θ/2 is tangent θ/2, which is then evaluated at π/2 and 0. The final result is 4/π, showcasing the average value of the function on the specified interval.
📘 Mean Value Theorem for Integrals and Its Graphical Interpretation
The final paragraph explains the Mean Value Theorem for Integrals, which states that for a continuous function on a closed interval [A, B], there exists a point C within the interval where the function's value at C times the interval length equals the integral of the function over the interval. This is visually represented as a rectangle with the same area as the area under the curve of the function. An example is provided using the function f(x) = √x over [0, 4], where the average value is calculated and a point C is found such that f(C) equals the average value. The paragraph concludes with a graphical representation of the function, the rectangle, and the area under the curve, illustrating the theorem's principle.
Mindmap
Keywords
💡Average Value
💡Integral
💡Anti-derivative
💡Chain Rule
💡Odd Function
💡Secant Squared
💡Mean Value Theorem for Integrals
💡Continuous Function
💡Rectangle Area
💡Graph Sketching
Highlights
The video explains how to compute the average value of a function and the Mean Value Theorem for integrals.
The average value of a function f(x) on an interval [A, B] is calculated as the integral from A to B of f(x) divided by the length of the interval (B - A).
An example is provided to find the average value of f(x) = sine(4x) on the interval from -π to π, resulting in an average value of 0.
The average value of sine(4x) is zero due to the function's odd symmetry about the origin.
The Mean Value Theorem for integrals states that for a continuous function on a closed interval, there exists a point C where the function's value equals the average value of the function over the interval.
The theorem is visually represented by a rectangle with the same area as the integral under the curve of the function.
An example demonstrates finding the average value of f(θ) = secant squared(θ/2) on the interval from 0 to π/2, resulting in 4/π.
The antiderivative of secant squared θ/2 is tangent θ, accounting for the chain rule.
The Mean Value Theorem for integrals is applied to f(x) = √x on the interval from 0 to 4, finding an average value of 4/3.
A value C is found such that f(C) equals the average value, leading to C = 16/9.
A graph is sketched to illustrate the Mean Value Theorem, showing the function √x and a rectangle with the same area as the integral from 0 to 4.
The importance of graphing to confirm the average value and the theorem's application is emphasized.
The video concludes with a summary of the lesson and an encouragement to practice the concepts.
The video provides a step-by-step guide to understanding the average value of a function and the Mean Value Theorem for integrals.
The process of anti-differentiation is explained with examples, showing how to find the antiderivative of sine(4x) and secant squared(θ/2).
The video uses graphical illustrations to confirm the theoretical results of the average value and the Mean Value Theorem.
The practical application of the Mean Value Theorem is demonstrated through the example of f(x) = √x, showing how to find a specific value C that satisfies the theorem.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: