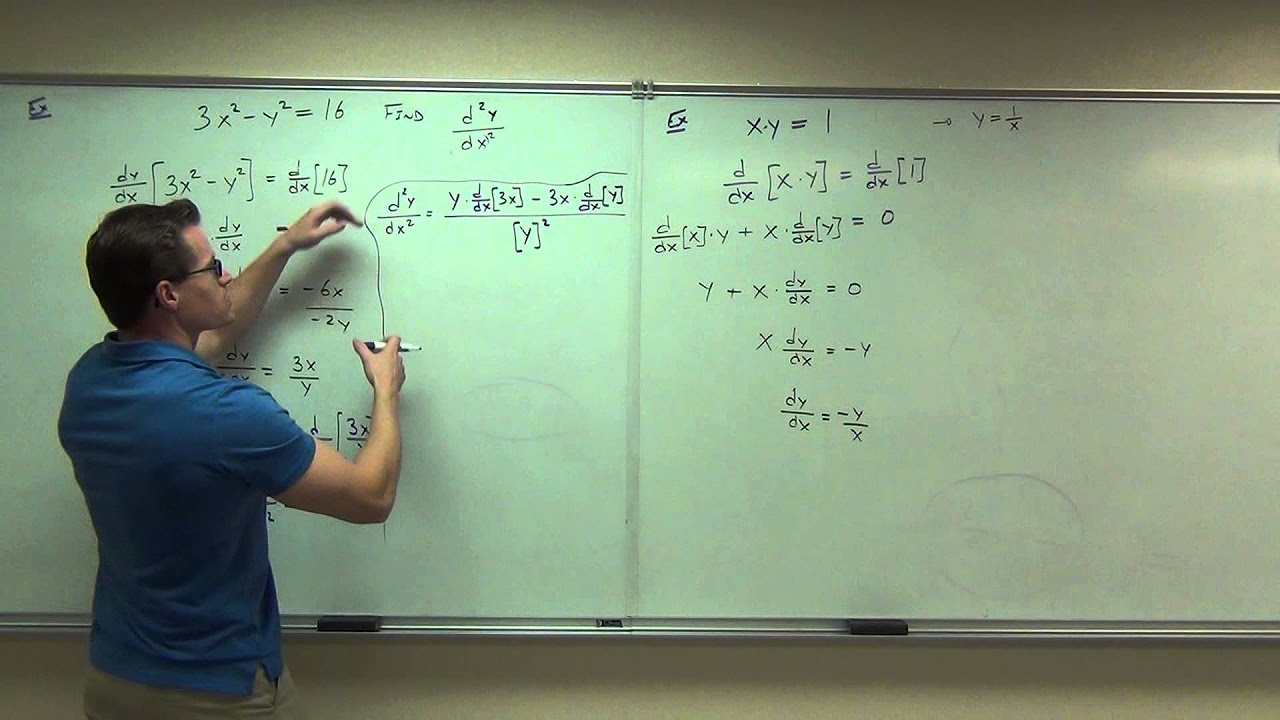Implicit Differentiation
TLDRThis video lesson delves into the concept of implicit differentiation, a method for finding the derivative of implicitly defined functions. The instructor starts by contrasting implicit differentiation with previous lessons on explicit functions and chain rule applications. The video covers examples of common implicit equations, such as the unit circle and hyperbola, and demonstrates the process of differentiating these equations step-by-step. It also discusses the use of implicit differentiation to find the slope of tangent lines and how to handle horizontal and vertical tangents. The instructor uses multiple examples to illustrate the concepts and encourages practice for better understanding, concluding with a look at how to determine concavity and the position of tangents relative to the curve.
Takeaways
- 📚 The video discusses implicit differentiation, a method used to find the derivative of equations where y is not explicitly expressed as a function of x.
- 🔍 The instructor emphasizes that the chain rule is fundamental to implicit differentiation, allowing for the differentiation of functions where the derivative of the inner function is not simply f or 1.
- 🌐 Examples of implicitly defined curves are provided, such as y^2 = x, x^2 + y^2 = 1 (the unit circle), x^2 - y^2 = 1 (the unit hyperbola), and ax^2 + by^2 = 1 (ellipses).
- 📉 The process of implicit differentiation involves taking the derivative of both sides of an equation with respect to x, isolating terms with dy/dx, factoring out dy/dx, and solving for dy/dx.
- 🧩 The video demonstrates how to find the slope of a tangent line to an implicitly defined curve by applying implicit differentiation and using the resulting formula for dy/dx.
- 🔄 The instructor corrects a mistake made in the process, highlighting the importance of careful differentiation and attention to variables, especially when dealing with product rules.
- 📌 The concept of horizontal and vertical tangents is introduced, explaining that horizontal tangents occur where the slope (dy/dx) is zero, and vertical tangents occur where the slope is undefined (due to division by zero).
- 📈 The video includes an example of using implicit differentiation to find the second derivative of a function, which can be used to determine concavity and thus whether a point is a local maximum or minimum.
- 📘 The instructor provides a method for determining whether a tangent line lies above or below a curve by examining the second derivative and its sign, indicating concavity.
- 🌟 The final example involves differentiating the equation sin(x) = e^y to find dy/dx in terms of x, demonstrating the substitution of e^y with sin(x) to simplify the expression to cot(x).
Q & A
What is the main topic of this video?
-The main topic of this video is implicit differentiation, which is the first lesson in Unit 4 of the course.
What is the difference between explicit and implicit functions?
-Explicit functions are written in the form y = f(x), where y is expressed directly in terms of x. Implicit functions, on the other hand, are equations where x and y are not explicitly separated, and they are defined by an equation involving both variables, such as y^2 - sin(2x) = 1.
Why is the chain rule important in implicit differentiation?
-The chain rule is important in implicit differentiation because it allows us to find the derivative of composite functions where the derivative of the inside of the function is not necessarily just f or the derivative isn't one.
What is the unit circle in the context of this video?
-The unit circle in this video refers to the equation x^2 + y^2 = 1, which is a circle with a radius of 1 centered at the origin. It is a fundamental concept in trigonometry.
What is the unit hyperbola and how is it related to hyperbolic trig functions?
-The unit hyperbola is the equation x^2 - y^2 = 1. It is where hyperbolic trig functions are derived from, similar to how the unit circle is related to trigonometric functions.
What is the process of finding the slope of a tangent line to an implicitly defined curve?
-The process involves taking the derivative of both sides of the equation with respect to x, moving all terms involving dy/dx to one side, factoring out dy/dx, and then solving for dy/dx by dividing.
How does the video explain the relationship between the slope of a radius and the slope of a tangent line to a circle?
-The video explains that the slope of a radius to a point on a circle (y/x) and the slope of the tangent line at that point (dy/dx) are perpendicular to each other, as indicated by their product being -1.
What is the significance of horizontal and vertical tangents in the context of this video?
-Horizontal and vertical tangents are significant because they represent points on a curve where the slope of the tangent line is zero (horizontal) or undefined (vertical). These points are often of interest in the analysis of curves.
How does the video demonstrate the process of finding the second derivative of a function?
-The video demonstrates this by taking the derivative of the first derivative (dy/dx) with respect to x, and then substituting the values of x and y to find the second derivative at a specific point.
What is the method used in the video to find the equation of a tangent line to a curve at a given point?
-The method involves finding the derivative of the curve (dy/dx) at the given point, using this derivative as the slope of the tangent line, and then using the point-slope form of a line to write the equation of the tangent line.
Outlines
📚 Introduction to Implicit Differentiation
This paragraph introduces the concept of implicit differentiation, which is the first lesson in Unit 4. The instructor explains that while previously derivatives were taken of explicit functions, implicit differentiation deals with equations where x and y are intertwined, such as y^2 = x or e^y = √x. The goal is to find the derivative dy/dx for these types of equations, which requires understanding the chain rule in a deeper context. The instructor also mentions common implicitly defined curves like the unit circle and hyperbola, and sets the stage for practicing derivative rules and investigating the chain rule further.
🔍 Derivative Rules and Chain Rule Application
The instructor delves into the specifics of taking derivatives using the chain rule, emphasizing the importance of recognizing when to apply it. Examples given include the derivative of f(x) squared and the derivative of 3x to the fourth with respect to t, highlighting the need to account for the derivative of the inner function. The paragraph reinforces the concept that the derivative of x with respect to x is 1, which is foundational in implicit differentiation. The instructor also provides practice problems for students to try on their own, encouraging them to apply the chain rule and product rule as necessary.
📈 Implicit Differentiation Process and Examples
This section outlines the steps for finding the derivative of an implicitly defined curve, including taking the derivative of both sides of the equation with respect to x, moving all terms involving dy/dx to one side, factoring out dy/dx, and solving for it. The instructor demonstrates the process with a specific equation and encourages students to try it with other examples. The importance of this technique is underscored as a means to find the slope of tangent lines to curves that are not explicitly defined in terms of y or x.
📘 Equation of a Tangent Line and Special Tangents
The instructor discusses how to write the equation of a tangent line to a curve at a given point, using the previously found derivative dy/dx. An example is provided where the slope of the tangent line to a specific curve at a given point is calculated, and the equation of the tangent line is derived. The concept of horizontal and vertical tangents is introduced, explaining that horizontal tangents occur where the slope is zero and vertical tangents occur where the slope is undefined due to division by zero.
🔑 Finding Points of Horizontal and Vertical Tangents
The paragraph focuses on identifying the points of horizontal and vertical tangents on a curve by setting the numerator of dy/dx to zero for horizontal tangents and the denominator to zero for vertical tangents. The instructor works through an example, solving for y when the derivative equals zero and when the denominator of the derivative equals zero to find the specific points on the curve. This method is crucial for understanding the behavior of curves at certain points and for further analysis such as drawing tangent lines.
📉 Second Derivative and Concavity
The instructor explains the process of finding the second derivative of a function to determine the concavity of a curve at a specific point, which is essential for understanding the curve's shape and identifying local maxima and minima. The second derivative test is highlighted, where a positive second derivative indicates concave up and a negative second derivative indicates concave down. An example is provided where the second derivative is calculated, and it is concluded that the curve has a local maximum at the given point due to the first derivative being zero and the second derivative being negative.
📌 Tangent Line Position and Implicit Differentiation Applications
The final paragraph discusses the position of a tangent line relative to a curve, whether it lies above or below, which is determined by the concavity of the curve. The second derivative is used to ascertain this, with a negative second derivative indicating the tangent line lies above the curve (since the curve is concave down). The instructor also provides a quick example of finding the slope of a tangent line for an equation where sine of x equals e to the power of y, demonstrating implicit differentiation and the use of substitution to express the derivative solely in terms of x.
Mindmap
Keywords
💡Implicit Differentiation
💡Chain Rule
💡Derivative
💡Tangent Line
💡Quotient Rule
💡Product Rule
💡Unit Circle
💡Ellipse
💡Hyperbola
💡Second Derivative
Highlights
Introduction to implicit differentiation as the first lesson in Unit 4.
Explanation of the chain rule's importance in differentiating composite functions.
Transition from explicit to implicit differentiation and its applications.
Examples of implicitly defined curves and their geometric interpretations.
Differentiation of basic equations like x = y^2 and x^2 + y^2 = 1.
Introduction of hyperbolic functions and their relation to the unit hyperbola.
The process of implicit differentiation involving the chain rule.
How to differentiate expressions involving e^y and the natural logarithm.
The quotient rule application in implicit differentiation.
Demonstration of finding the slope of a tangent line on implicitly defined curves.
Steps for finding dy/dx on implicitly defined curves through examples.
How to write an equation for a tangent line given a point and a slope.
Analysis of horizontal and vertical tangents using dy/dx.
Solving for the second derivative to determine concavity and local extrema.
Using the second derivative test to find local maxima and minima on a curve.
Differentiating the equation sine(x) = e^y to express dy/dx in terms of x only.
Substitution techniques to eliminate e^y in differentiation to express in terms of x.
Concluding remarks summarizing the process and applications of implicit differentiation.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: